, (1)
где S(jω) - спектр полезного сигнала; (...)*- знак комплексного сопряжения; T - длительность полезного сигнала; с - произвольная ненулевая константа.
Для небелого гауссовского шума со спектральной плотностью мощности N(jω) оптимальным является каскадное включение обеляющего и согласованного фильтров с совместной передаточной функцией [1]:
, (2)
При неизвестном спектре помехи использование (2) становится невозможным.
Предлагаемый метод заключается в адаптивной нелинейной обработке F(Y) спектра входной смеси сигнала с помехой Y(jω)=X(jω)+ S(jω). Для изложения его сути перейдём от непрерывных функций частоты к их дискретным отсчётам: Sk=S(jωk) , Xk=X(jωk) , Yk=Y(jωk), KLk=KL(jωk) и т.д.
В качестве критерия адаптации выберем минимум среднего квадрата ошибки воспроизведения модуля спектра полезного сигнала на выходе нелинейной обработки F(Y):
. (3)
Очевидно, что поиск оптимальной функции FOPT(Y), обеспечивающей минимум (3) равный нулю, приводит к выражениям для характеристики нелинейного преобразования и коэффициента передачи нелинейного СФ:
, 
. (4)
Для сравнительной оценки эффективности используем отношение энергии сигнала к энергии помехи на выходе каждого из трёх фильтров:
, (5)
где L=1,2,3, - номер передаточной функции фильтра.
Эффективность (5) предлагаемого метода была исследована моделированием в среде MatCAD на примере приёма одиночного радиоимпульса с частотой заполнения 
на фоне помехи в виде аддитивной смеси гауссовского шума с дисперсией σ2 и синусоидального колебания постоянной амплитуды Ax с центральной частотой спектра 
и модуляцией по фазе по закону синуса с частотой 
и индексом 
. Радиоимпульс амплитудой As и длительностью 
был задержан относительно начала приёма на время 
. Здесь 
- частота дискретизации, а 
- шаг дискретизации. Параметры модуляции сигнала и помехи были выбраны таким образом, чтобы их спектры перекрывались. Изменяли степень «негауссовости» α= Ax2/2σ2 , а также отношение сигнал-помеха на входе q0=2As2/( Ax2+2σ2).
В табл. 1 представлены результаты исследований в виде выигрыша μ3 = q3/q1 для различных q0 и α (в децибеллах).
Таблица 1
|
q0 α |
-30 |
-20 |
-10 |
0 |
10 |
|
-10 |
12.36 |
7.77 |
7.94 |
4.93 |
0.79 |
|
0 |
6.05 |
5.54 |
0.15 |
-0.45 |
-0.16 |
|
10 |
10.99 |
5.23 |
6.59 |
4.67 |
-0.08 |
|
20 |
13.48 |
11.26 |
12.25 |
6.05 |
0.38 |
На рис. 1 представлены графики отсчётов огибающей на выходе рассмотренных выше СФ для q0 = -20дБ и α =20дБ (номер графика соответствует номеру передаточной функции, цифра по горизонтали - номеру отсчёта).
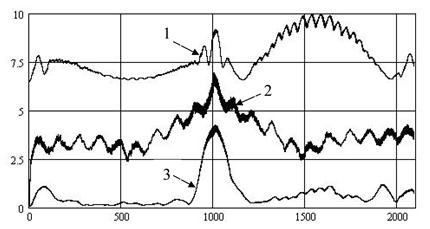
Рис. 1. Отсчёты огибающей отклика согласованных фильтров
Полученные результаты исследований позволяют сделать следующие выводы:
- эффективность предлагаемого СФ по сравнению с обычным существенно зависит от параметра помехи (для q0= -10 дБ μ3≈0 дБ при α=0 дБ и μ3≈12 дБ при α=20 дБ);
- предлагаемый СФ наиболее эффективен при малом отношении сигнал-помеха (μ3≈14 дБ для q0= -30 дБ и α=20 дБ); для «мощных» сигналов его эффективность совпадает с обычным СФ;
- предлагаемый СФ может существенно (от 7 до 20 дБ) проигрывать СФ, оптимальному при небелом шуме с известным спектром мощности;
- форма отклика предлагаемого нелинейного СФ в отличие от обычного линейного соответствует ожидаемой, а именно: положение максимума отклика нелинейного СФ соответствует ожидаемому, т.е.
; - предложенный в статье метод нелинейной согласованной обработки сигналов достаточно прост в реализации и позволяет существенно (на 10...20 дБ) повысить помехоустойчивость радиотехнических систем.
СПИСОК ЛИТЕРАТУРЫ
- Гоноровский И.С. Радиотехнические цепи и сигналы: учебник для вузов / И.С. Гоноровский. М.: Сов. радио, 1977. 608 с.