Анализ опубликованных в научной литературе исследований, как российских, так и зарубежных авторов, о влиянии частоты циклического нагружения на прочность и долговечность деталей машин и конструкций не дает исчерпывающей информации. Существует мнение, что изменение частоты не оказывает значительного влияния на сопротивление усталости материалов, хотя признается некоторая тенденция к увеличению сопротивления усталости материалов при увеличении частоты нагружения [5-6]. Недостаточность фундаментальных знаний о факторе частоты циклов объясняется в первую очередь сложностью физических процессов [1], происходящих в поверхностном слое металлов, и длительностью эсперимента. Требуется более детальное изучение этого вопроса, поскольку при циклическом нагружении речь идёт о пластической деформации в поверхностных слоях.
С поверхностными эффектами это согласуется следующим образом. Поверхностный слой деформируется раньше массива твердого тела [4]. Чем легче деформируется поверхностный слой, тем сильнее повреждается поверхность материала, т.е. тем больше повреждаемость Ф. Повреждаемость активного слоя и собственно поверхности описывается выражением вида [1-4]:
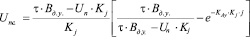, (1)
где τ – напряжение действующее на петлю дислокации; Вд.у. – площадь дефекта упаковки;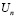 
– энергетический порог повреждаемости собственно поверхности; 
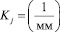– параметр, связанный обратной зависимостью с поперечным размером (толщиной) поверхностного слоя j; 
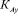– параметр, определяющий сопротивление среды прохождению физического процесса пластической деформации, параметр упрочнения материала поверхностного слоя.
Целью представленной работы является изучение влияния частоты циклического нагружения на сопротивление пластической деформации в поверхностных слоях металлических материалов.
Достаточно сложные явления, протекающие в поверхностных слоях образцов (деталей) при изменении частоты циклического нагружения, можно соотнести с представлением о суммарной деформации ɛω, которая накапливается при усталостных испытаниях в поверхностных слоях глубиной j (формула (1)). Она связывается с количеством циклов N и определяется углом наклона левой ветви кривой усталости αω. Эта связь в первом приближении может быть представлена как изменение суммарного накопления усталостных дефектов или повреждений решётки dZ:
dZ = dZ1 – dZ2, (2)
где dZ1 – увеличение плотности (количества) дефектов вследствие накопления суммарной деформации ɛω; dZ2 – уменьшение плотности дефектов вследствие релаксации.
При этом вносится определённое допущение, связанное с тем, что релаксация напряжений не всегда связана с уменьшением концентрации дефектов. Например, в случае повторяющихся актов поперечного скольжения, возникающие в полосах скольжения интрузии приводит к увеличению вероятности разрушения тем в большей степени, чем больше энергия дефекта упаковки (γ) [1].
Конечное выражение этой зависимости представляется в виде соотношения:
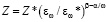, (3)
связывающего суммарное повреждение Z с величиной суммарной деформации ɛω и частотой циклов (ω), где Z* = Z, а ɛω*= ɛω для одного цикла напряжения; β – зависит от рода вещества; α – видимо, должна возрастать с температурой, но уменьшаться с увеличением энергии дефекта упаковки.
Если считать, что между ɛω и числом циклов до разрушения существует прямая пропорциональность, то, когда для достаточно низких гомологических температур (θ) отношение α/ω стремится к нулю, продолжительность испытаний определяется числом циклов. Напротив, при достаточно высоких θ величина Z обусловливается как ɛω (или N), так и частотой ω, то есть с увеличением температуры величина накопленных напряжений, а следовательно, и продолжительность испытаний всё больше определяется не числом циклов, а временем, причём Z оказывается тем больше (время до разрушения тем меньше), чем больше частота циклов. Из уравнения (3) также следует, что
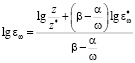, (4)
то есть увеличение частоты приводит в общем к снижению ɛω (или N).
Выводы
1) увеличение частоты снижает суммарную деформацию ɛω;
2) влияние частоты на ɛω с увеличением θ становится слабее.
3) cнижение суммарной деформации ɛω сопровождается снижением коэффициента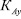 
, что в свою очередь снижает энергетический порог Uп.с. (формула (1)).
4) Повреждаемость поверхностного слоя усиливается, и наклон левой ветви кривой усталости растёт. С увеличением θ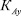 
снижается, что в конечном итоге замедляет снижение энергетического порога Uп.с. и, естественно, влияние частоты становится менее ощутимо. Это означает, что в случае больших θ снижение ɛω должно быть меньше, чем в случае малых θ, соответственно увеличение частоты в первом случае должно привести к увеличению напряжения и, наоборот, во втором случае увеличение ω может снизить напряжение.