Изучив процесс оптимизации (см. об этом подробнее [5, стр. 35 – 58]), нами была получена теория получения его схемы замещения (см. о ней в статьях [2, 3]).
Далее была произведена замена реальной системы (РС) на эквивалентную схему замещения (см. об этом подробнее [2]). После чего была получена техническая система (ТС) процесса оптимизации (см. об этом в статье [3]).
Теперь можно произвести анализ связей между элементами в этих двух системах. Это необходимо для определения того, как качественно изменилась новая (ТС) по отношению к существующей РС. Данный анализ позволит доказать необходимость производимой замены.
Цель исследования – выявления характера изменения прямых и обратных связей, а так же связей порождения, структурных и связей функционирования в РС и ТС процесса оптимизации. Это поможет понять, как повлияла замена РС технической, на структуру процесса оптимизации. И доказать правомерность и пользу данной замены.
Материалы и методы исследования
Сначала произведём анализ прямых и обратных связей в РС и ТС процесса оптимизации.
Связи взаимодействия или координации между элементами в этих системах не что иное, как прямые и обратные связи. Производить анализ этих связей удобно по схеме замещения РС процесса оптимизации [2]. Пусть прямые связи – это линии, имеющие направление слева на право, а обратные связи – это линии, идущие справа налево.
При фиксированном числе элементов n в системе, общее число возможных прямых и обратных связей складывается из следующих вариантов:
– программа «Оптимэль» [4], реализующая ТС процесса оптимизации: 2 связи;
– идеальный случай, когда каждый элемент процесса оптимизации заканчивается положительным результатом, а выбранный метод оптимизации подошёл к решению оптимизационной задачи: 6 связей или n+1;
– не идеальный случай, когда один или несколько элементов процесса оптимизации могут быть пропущены по разным причинам или изменена последовательность выполнения процессов.
Чтобы проанализировать, как изменяется число прямых и обратных связей в зависимости от числа элементов в процессе оптимизации, необходимо было добавлять в схему замещения РС по ещё одному процессу и следить за изменениями в системе, подсчитывая число возможных вариантов перехода для не идеального случая. Следует проанализировать эти переходы, выявить закономерности и по полученным данным построить зависимость. Эти данные были вынесены в таблицу 1. Были рассмотрены схема с разным числом элементов n.
Пусть всегда первый (литературно-патентный обзор) и последний (выбор метода оптимизации) процессы участвуют в переходе, так как они фиксированы, а остальные нет. Пускай при любом числе элементов в процессе оптимизации меняются местами лишь второй и третий процессы, тогда эту зависимость числа прямых связей от числа элементов в процессе можно представить так: n.
Поэтому число возможных вариантов перехода для каждого из оставшихся случаев можно разбить на две составляющие – это центральное уменьшение числа элементов: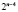 
, и боковое уменьшение числа элементов: 
.
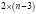Все возможные переходы для не идеального случая – это
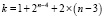. (1)
Получим теперь приблизительное число прямых связей для каждого случая в отдельности, умножив число возможных вариантов перехода определённого случая на среднее число прямых связей для этого случая:
– 
;
– 
.
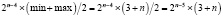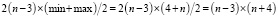Тогда число возможных прямых связей для не идеального случая, зависящее от числа элементов в процессе оптимизации будет равно
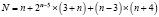. (2)
Будем подставлять значения n в (1) и (2) от 5 до 15. Значения занесём в табл. 1.
Таблица 1
Зависимость числа прямых связей N для не идеального случая от числа элементов в процессе оптимизации n
|
n |
5 |
7 |
9 |
11 |
15 |
|
N |
31 |
91 |
279 |
1027 |
18660 |
|
k |
7 |
17 |
45 |
145 |
2073 |
|
N/k |
4,4 |
5,3 |
6,2 |
7,1 |
9 |
Как видно из табл. 1, N принимает достаточно большие значения при n = 7 и 9.
При последовательном расположении элементов (см. рис. статьи [2]) на листах формата А4 (если количество переходов для не идеального случая достигает k=17), он должен быть альбомным. Дальнейшее увеличение k делает проблемным изображение на рисунке процесса оптимизации, как целиком, так и по частям, даже при использовании преобразованной схемы замещения реальной системы процесса оптимизации [2].
Схема замещения с n=5 является наиболее подходящей (см. рис. статьи [2]), так как на одной линии одного варианта перехода можно отобразить до n связей, тогда как на других схемах нужно каждую прямую связь отображать отдельно. То есть вместо k линий нужно изобразить N количество, что в <<popova7.wmf>> раз больше чем k (см. табл. 1).
Понятно, что для выявления необходимых закономерностей и ожидаемых зависимостей, число элементов в процессе оптимизации может быть при желании увеличено, но не более чем до 7 элементов. Так как дальнейшее увеличение элементов не рационально, из-за большой вероятности путаницы в огромном числе переходов, прямых связей, чревато тратой излишнего числа времени на исследование этих закономерностей. Так же возможны из-за этого недочёты и незамеченные ошибки.
Для устранения этих неудобств, потребуется вводить определённые ограничения (что сократит число связей). Это снизит желаемую точность в выявлении закономерностей и искомых зависимостях. Всё это касается визуального анализа, когда схема отображается на листе перед учёным и анализ схемы он проводит самостоятельно без участия ЭВМ.
Чтобы просчитать закономерности и искомые зависимости в реальной системе процесса оптимизации между её элементами, число которых превышает n=7, можно составить алгоритм, который будет использовать программа. А чтобы избежать недочётов, незамеченных ошибок, неизбежных ограничений, для составления алгоритма можно использовать РС процесса оптимизации с числом от 5 до 9 элементов.
Выявить закономерности позволит увеличение числа вариантов перехода в схеме и с небольшим числом элементов. А получение искомых зависимостей станет возможным за счёт исследования схем сначала с n=5, потом n=6 и так далее до n=8.
Примером может быть исследование на выявление зависимостей числа вариантов перехода и прямых связей от числа элементов в процессе оптимизации.
Если перед учёным будет стоять комплексная задача исследования процесса оптимизации, то наиболее оптимальное решение – это использование пяти элементов в реальной системе процесса оптимизации. Тогда выявление закономерностей и зависимостей можно проводить за счёт выяснения того, как влияет прямая связь, поступающая на вход одного элемента процесса, на его внутреннюю структуру. См. об этом [5, с. 73 – 75].
Результаты исследования и их обсуждение
Изучив РС и ТС [5] процесса оптимизации, произведём анализ их связей. В идеальном случае для двух систем все связи являются связями порождения, так как каждый элемент вызывает к жизни другой, идущий за ним элемент, с положительным результатом на выходе. В не идеальном случае, та прямая связь, которая отошла от элемента после увеличения его объёма до или больше оптимального, может считаться связью порождения. См. об этом подробнее [5, с. 73]. Тогда, в неидеальном случае, связи порождения могут сформировать цепочку прямых связей идеального случая, то есть не идеальный случай стремиться к идеальному в реальной системе процесса оптимизации, посредством увеличения объёма его элементов за счёт применения обратных связей [5, с. 74, 75].
Теперь предположим, что имеет место элемент, объём которого равен сумме оптимальных объёмов всех пяти элементов процесса оптимизации [5]. Тогда на выходе из него должен быть получен положительный результат, если удастся должным образом подобрать и сформировать имеющиеся знания о методах оптимизации. У данного элемента будут свои связи строения (или структурные связи), отличающиеся от структурных связей РС процесса оптимизации. Этот элемент в ТС процесса оптимизации использован для решения проблемы сокращения времени выбора метода оптимизации [5, с. 5 – 8].
Поэтому закладывание структуры РС процесса оптимизации в алгоритм программы «Оптимэль» [4] (которая находит оптимальный метод оптимизации для решаемой задачи) будет не целесообразным решением проблемы, из-за не значительного сокращения времени выбора метода оптимизации. Значительное сокращение времени возможно за счёт применения новой структуры, отличающейся от структуры РС процесса оптимизации.
Как видно из выше сказанного, все прямые и обратные связи между элементами процесса оптимизации образуют структуру РС (см. рис. структуры в статье [2]). В ТС все пять элементов процесса оптимизации должны протекать одновременно. Литературно-патентный обзор, изучение математических моделей и методов оптимизации, сравнение методов и сам выбор одного из методов можно соединить воедино, если использовать систему вопросов и ответов. См. о ней подробнее [3]. Данная система имеет структуру бинарного дерева – дедуктивная система (см. так же [2, 6]). Идейный смысл данной структуры позволяет на этапе формирования дерева отсортировать знания о методах оптимизации таким образом, чтобы среди них можно было быстро и легко отыскать нужный метод, подходящий для решения задачи, по имеющимся данным о задаче исследования. Система вопросов и ответов [3, 6] сформулирована так, что во время ответа на поставленный вопрос происходит уточнение изначальных данных о задаче оптимального исследования, что позволяет определить под конец, каким методом её можно решить.
Таким образом, из общего объёма знаний обо всех методах оптимизации выбирается знание, содержащие информацию об оптимально подходящем методе к решаемой задаче оптимизации. Получается, что ТС смогла отразить в себе общую идею, заложенную в РС процесса оптимизации – из знания о методах оптимизации выбрать знание о подходящем методе для решения оптимизационной задачи. См. об этом подробнее [3].
В РС процесса оптимизации связи функционирования – это комбинация прямых и обратных связей, индивидуальная для каждого случая. Эти связи отражают переход от одного процесса к другому, в зависимости от необходимой функции выполнения в данный момент. Если необходимо увеличить объём знания, то обратная связь идёт к нужному элементу, где надо пополнить знания. Если нужно выполнить следующее по смыслу действие, то происходит переход к следующему элементу, а может и через элемент. Здесь переходы по связям функционирования во многом зависят от человеческого фактора, который может повлиять на количество прямых и обратных связей. Каждая такая комбинация составляется из структурных связей РС.
В ТС связи функционирования – это переходы по бинарному дереву системы вопросов и ответов сверху вниз. Каждый переход – это ответ на один вопрос. Тогда число связей функционирования зависит от числа пройденных вопросов. Если должным образом составить систему вопросов и ответов, то число связей функционирования будет минимальным. Для этого будем использовать идею, заложенную в дерево Хаффмана (использующуюся для кодирования данных). Составить вопросы таким образом, чтобы наиболее часто используемые методы оптимизации оказались на более высоком уровне.
Так же нужно постараться, чтобы дерево было максимально равновесно, а число вопросов до нижних уровней минимально.
Понятно, что число связей функционирования и их последовательность в РС процесса оптимизации отражает число процессов выполненных в системе в определённом порядке. Тогда время, потраченное на их выполнение – это их суммарное время выполнения. Здесь время, затраченное на выполнение одного процесса, зависит от человеческого фактора, сложности задачи и так далее, и может продолжаться от одного часа до нескольких лет. В ТС процесса оптимизации новые связи функционирования соединяют вопросы. Следовательно, суммарное время ответов на вопросы – это время, затраченное на определение подходящего метода оптимизации. Если учёный мотивирован на получение результата, то предоставленная система подсказок позволит ему дать ответы в наиболее сжатые сроки. Учёный должен понять вопрос, проанализировать свою задачу оптимизации, принять решение. И так несколько раз в зависимости от выбранного варианта ответа. Следовательно, система вопросов и ответов должна быть понятна, информативна, интуитивна и так далее.
Число новых связей функционирования зависит от высоты расположения искомого метода оптимизации на дереве. Так, например, если метод расположен на g уровне, то число новых связей функционирования будет равно g-1. На такое же число вопросов он должен будет и ответить. Так, например, в системе вопросов и ответов [5, с. 77; 6] программы «Оптимэль» максимально возможное число новых связей функционирования – 14. Поэтому новую функциональную связь можно считать прямой связью ТС процесса оптимизации.
Максимальное число новых прямых связей (все прямые связи в дереве) зависит прямо пропорционально от суммы всех вопросов в системе и всех методов оптимизации. В разработанной системе вопросов и ответов – это сумма промежуточных узлов (5, стр. 86) и листов дерева (5, с. 87), то есть 63 + 63 = 126. Общая система прямых связей образует структурные связи между элементами ТС процесса оптимизации. Они имеют вид бинарного дерева, где входом в систему является корень дерева, а выходом из неё – соответствующий лист дерева, то есть метод оптимизации. Тогда решением будет являться путь по дереву от корня к листу, то есть соответствующая комбинация связей функционирования или прямых связей.
Возвращение к корню дерева возможно в том случае, если учёный ошибочно ввёл не тот ответ. По смыслу выполнения – это новая обратная связь.
Понятный интерфейс программы позволяет вернуться к нужному вопросу за считанные минуты. Следовательно, обратные связи в программе «Оптимэль» – это в основном ошибки ввода, минимизировать влияние которых можно программным образом. Поэтому их в расчёте времени выполнения программы «Оптимэль» можно не учитывать. Тогда можно принять, что новые связи функционирования совпадают со связями порождения в ТС.
Выводы
Исследование связей в РС и ТС показало, что в ТС число всех возможных прямых связей равно числу узлов в дереве системы вопросов и ответов. Общая система прямых связей отражает структуру бинарного дерева системы вопросов и ответов. Тогда полученное решение (путь по дереву от корня до нужного листа) – это последовательность связей функционирования, которые являются прямыми связями.
В РС число прямых связей значительно возрастает с увеличением числа элементов в схеме (см. табл. 1). Было выявлено оптимальное число элементов РС – это n = 5. Тогда структурные связи в РС – это все возможные варианты прямых и обратных связей между этими элементами (см. рис. в статье [2]). А комбинация структурных связей (прямых и обратных связей) для каждого конкретного случая – это связи функционирования.
Связи взаимодействия или координации между элементами в РС и ТС – это те же прямые и обратные связи.