Scientific journal

International Journal of Experimental Education

ISSN 2618–7159

ИФ РИНЦ = 0,425

Задача о максимальном потоке в сети изучается уже более 60 лет. Интерес к ней подогревается огромной практической значимостью этой проблемы. Методы решения задачи применяются на транспортных, коммуникационных, электрических сетях, при моделировании различных процессов физики и химии, в некоторых операциях над матрицами, для решения родственных задач теории графов, и даже для поиска Web-групп в WWW.

Основным в теории потоков является понятие сети. Сеть – это взвешенный конечный граф без циклов и петель, ориентированный в одном общем направление от вершины I, являющейся входом (истоком), к вершине S, являющейся выходом (стоком) графа. Пример сети показан на рис. 1. Для наглядности будем представлять, что по ребрам (i, j) сети из истока I в сток S направляется некоторый ресурс (груз, нефть, информация и т. п.). В теории потоков предполагается, что если ребро (i, j) входит в сеть, то в сеть входит и ребро (j, i). Ребрам сети присваивается одна или несколько числовых характеристик.

Общее количество вершин сети будем обозначать через n. На рис. 1 истоком I является вершина 1, стоком S вершина 6.

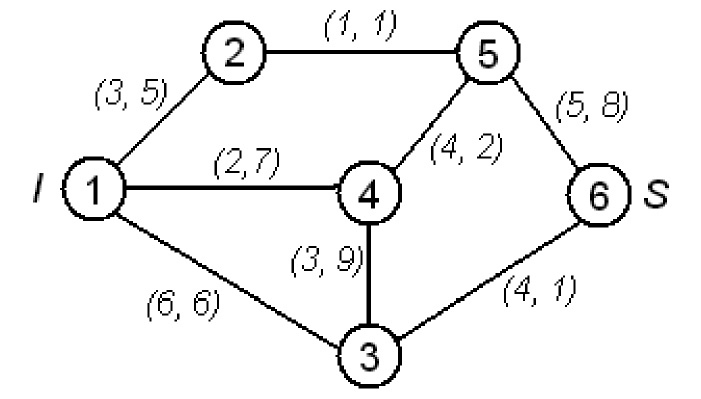
Рис. 1. Пример транспортной сети с шестью вершинами

Максимальное количество rij ресурса, которое может пропустить за единицу времени ребро (i, j), называется его пропускной способностью. В общем случае rij≠rji. Если вершины k и l на сети не соединены, то rkl=rlk=0. На сети (рис. 1) пропускные способности ребер указаны в скобках. При этом первое число – это пропускная способность в направление от вершины i к вершине j, второе – в противоположном направление. Пропускные способности сети можно задать квадратной матрицей R n-го порядка. Поскольку rii=0, на главной диагонали стоят нули.

Количество хij ресурса, проходящего через ребро (i, j) в единицу времени, называется потоком по ребру (i, j).

Произвольно задать n2 чисел xij
(i, ) нельзя. Они должны подчиняться определенным ограничениям, о которых речь пойдет дальше. А пока будем считать, что если поток из вершины i в вершину j равен xij, то поток из вершины j в вершину i будет равен -xij, т. е.:

xji=–xij. (1)

Если поток xij по ребру (i, j) меньше его пропускной способности, т.е. xij<rij, то ребро (i, j) называется ненасыщенным, в противном случае оно называется насыщенным.

Совокупность X={xij} потоков по всем ребрам (i, j) сети называют потоком по сети или просто потоком.

Из физического смысла грузопотока следует, что поток по каждому ребру (i, j) не может превышать его пропускную способность, т. е.:

xij≤rij (i, ). (2)

Понятно также, что для любой вершины, кроме истока I и стока S, количество вещества, поступающего в эту вершину, равно количеству вещества, вытекающего из нее. С учетом соглашения (1) это требование можно выразить записью:

(i≠I,S). (3)

Это ограничение называют условием сохранения потока: в промежуточных вершинах потоки не создаются и не исчезают. Отсюда следует, что общее количество вещества, вытекающего из истока I, совпадает с общим количеством ресурса, поступающим в сток S, т.е.:

, (4)

где j – конечные вершины ребер, исходящих из I; i – начальные вершины ребер, входящих в S.

Линейную функцию f называют мощностью потока на сети.

Учитывая сказанное, задачу о максимальном потоке можно сформулировать следующим образом: найти совокупность X={xij} потоков xij≥0 по всем ребрам (i, j) сети, которая удовлетворяет условиям (1) – (3) и максимизирует линейную функцию (4). Это типичная задача линейного программирования.

Пусть дана некоторая сеть. Разобьем множество вершин сети на два непересекающихся подмножества А и В так, чтобы исток I попал в подмножество А, а сток S – в подмножество В. В этом случае говорят, что на сети произведен разрез, отделяющий исток I от стока S. В результате произведенного разбиения вершин появятся ребра (i, j), конечные точки которых окажутся в разных подмножествах. Совокупность ребер (i, j), начальные точки которых принадлежат подмножеству А, а конечные – подмножеству В, называют разрезом сети и обозначают А/В.

Введем важные определения.

Величина:

представляет собой сумму пропускных способностей rij всех ребер разреза, называется пропускной способностью разреза.

Пусть на сети задан поток X={xij} и произведен разрез А/В. Величина

представляет собой сумму потоков xij по всем ребрам разреза, называется потоком через разрез.

Оказывается, что если удается построить на сети поток X={xij}, величина которого равна пропускной способности некоторого разреза А/В, то этот поток будет максимальным, а разрез А/В обладает минимальной пропускной способностью.

Справедлива следующая теорема Форда – Фалкерсона, которая имеет важное прикладное значение. На любой сети максимальная величина потока из истока I в сток S равна минимальной пропускной способности разреза, отделяющего I от S. Доказательство приведено, например, в [2].

Алгоритм Форда-Фалкерсона был предложен в 1956 г. До этого времени задача решалась с помощью методов линейного программирования, что было не эффективно.

Алгоритм начинает свою работу с нулевого потока и на каждой своей итерации увеличивает поток в сети. На каждом шаге находится увеличивающая величину потока цепь. Поток увеличивается вдоль дуг этой цепи, пока она не станет насыщенной.

Увеличивающей цепью является цепь из истока в сток, все дуги которой допустимы. Дугу из вершины i в вершину j назовем допустимой, если выполняется одно из следующих условий:

1) xij<rij и дуга согласованна;

2) rij>0 и дуга несогласованна.

По увеличивающей цепи можно пустить поток величины Q, где Q = min{qi, 1 ≤ i ≤ l} и qi = {xij – rij}, если дуга согласованна, xij, если дуга не согласованна}. Для того, чтобы увеличить величину потока сети на Q, необходимо увеличить на Q поток на каждой согласованной дуге цепи и уменьшить на каждой несогласованной.

В своей работе Форд и Фалкерсон доказали, что поток в сети, для которой нельзя построить увеличивающую цепь, является максимальным.

Для нахождения увеличивающей цепи ими был предложен «Метод расстановки пометок» [2], который и взят за основу для реализации решения задачи о максимальном потоке, посредством сетей Петри.

Решение задачи о максимальном потоке с помощью обыкновенных сетей Петри

Рассматриваемый в этом пункте метод предполагает ряд ограничений для сети:

– целочисленные пропускные способности на дугах;

– наличие одного истока и одного стока;

– пропускные способности вершин не ограничены;

– нижние пределы потоков по дугам не заданы;

– дуги могут обладать различными пропускными способностями в различных направлениях.

В случае если одно или несколько условий не выполняется, необходимо сначала преобразовать заданную транспортную сеть, а затем преобразованную сеть смоделировать.

Задачу о максимальном потоке также можно рассмотреть на обыкновенной сети Петри [4, 5].

В качестве примера смоделируем транспортную сеть, показанную на рис. 1, сетью Петри.

Не нарушая общности, для любой транспортной сети предлагаются следующие правила построения сети Петри:

• каждой вершине i транспортной сети в сети Петри заводится позиция с именем i (вершина 1 называется «istok», а последняя вершина «stok»);

• взамен дуги в ориентированном графе от вершины i к вершине j , в сети Петри создаются два перехода “i-j” и “j-i” и две позиции “psi-j” и “psj-i”, которые содержат количество фишек, равное пропускной способности дуг (i,j) и (j,i) rij и rji;

• посредством этих переходов реализуется движение, если вперед, то фишка забирается из “psi-j” и добавляется в “psj-i” если назад, то фишка добавляется в “psi-j” и забирается из “psj-i”;

• роль ресурса транспортной сети будут выполнять фишки, единица ресурса – одна фишка. Изначально фишка будет находиться в истоке.

• из сети исключены дуги, исходящие из стока, поскольку они не имеют смысла. А от переходов, указывающих на сток, проложены стрелки, возвращающие фишку ресурс в исток.

По данным правилам мы можем для любой транспортной сети построить сеть Петри. В частности для нашего примера, получается сеть Петри, представленная на рис. 2.

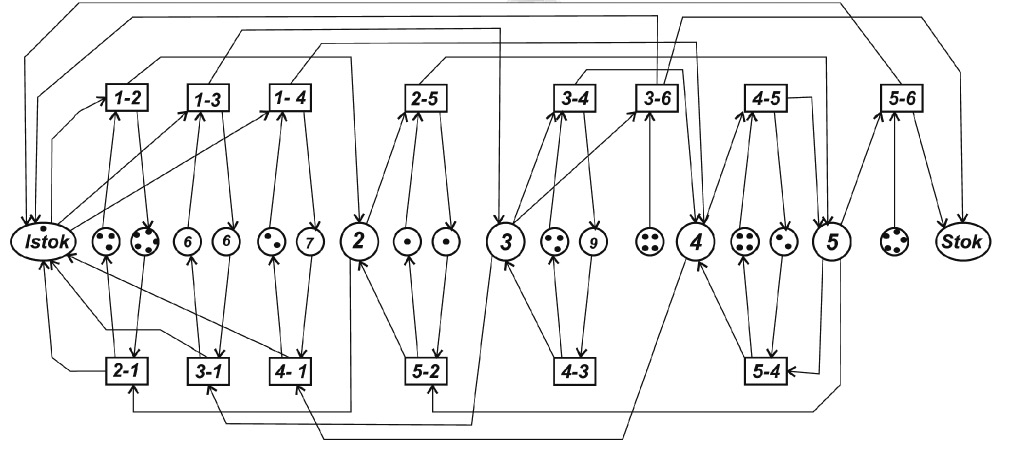
Рис. 2. Сеть Петри, соответствующая транспортной сети

На этом рисунке верхний ряд переходов соответствует согласованным дугам (от вершины с меньшим индексом к вершине с большим индексом), нижний ряд – несогласованным. Позиции «istok» и «stok» соответствуют вершинам 1 и 6, позиции 2, 3, 4, 5 одноименным вершинам соответственно. Маркировки позиций в середине рисунка соответствуют пропускным способностям дуг (i, j). Основным недостатком является случайность срабатывания переходов. В результате длительных метаний фишки будут попадать все-таки в сток, так что результат будет получен верный. В конце концов, сеть зайдет в тупик и в стоке число фишек будет равно максимальному потоку транспортной сети.

Результат работы сети после 130 шагов будет достигнут и максимальный поток сети на рис. 1 равен 9.

Кроме того возможно распараллеливание процессов, для этого необходимо в исток поместить достаточно большое количество фишек и разрешить одновременное срабатывание нескольких переходов. В этом случае необходимое количество тактов работы сети Петри значительно уменьшится. Так при введении в исток 11 фишек, результат был достигнут уже на 40 шаге. Правда, сеть может не заходить в тупик, поэтому необходимо останавливать сеть после достаточно большого числа срабатываний.

Применение динамических приоритетов

Решение, представленное в предыдущем пункте, обладает существенным недостатком: фишка от истока в сток идет не кратчайшим возможным путем, а попадает в результате случайных метаний. Идея – избежать таких метаний, с помощью введения классических приоритетов, например, задания приоритетов для согласованных и несогласованных переходов, не может привести к приемлемым результатам, поскольку тупиковые пути приведут к зацикливанию алгоритма. Не допустить подобного зацикливания позволит введение динамических (постоянно меняющихся) приоритетов. Т.е. после срабатывания любого перехода, полностью пересчитываются вся таблица приоритетов, по определенному алгоритму. Возможно также одновременное применение нескольких динамических приоритетов.

В таком случае потребуется создание массива приоритетов, где самым старшим приоритетом будет приоритет с индексом 1 и т.д. При этом если есть несколько рабочих переходов с одинаковыми приоритетами первого уровня, проверяются их приоритеты второго уровня и так далее. Если все приоритеты равны, то переход срабатывает случайным образом, либо если возможно параллельное выполнение сработают оба перехода. Если хотя бы один из приоритетов имеет значение 0, то переход не может сработать вовсе.

Для реализации алгоритма Форда-Фалкерсона мы будем использовать три уровня приоритетов.

Приоритетом первого уровня будет «флаговый» приоритет, он будет служить для предотвращения возникновения циклов. Изменение этого приоритета можно задать тремя правилами:

1) Изначально все переходы имеют значение 1.

2) При срабатывании перехода «i-j», когда j не является стоком, все переходы «x-i» (где x любая позиция кроме j), получают приоритет 0.

3) При срабатывании перехода «i-j», когда j является стоком, все переходы приобретают приоритет 1.

Приоритетом второго уровня будет числовой приоритет. Главной задачей числового приоритета будет отслеживание возникающих тупиков при моделировании сети. При этом рабочий переход будет влиять как на свой приоритет, так и на приоритет обратного перехода, кроме того, приоритет после срабатывания будет зависеть от приоритета до срабатывания – как прямого так и обратного переходов. Правила изменения численных приоритетов сведены в таблицу.

Правила изменения числовых приоритетов

В таблице Ppr это приоритет прямого перехода, Opr – обратного. Изначально, приоритеты переходов указывающих на сток равны 5, а остальные равны 3.

При срабатывании перехода, указывающего на сток, происходит конец цикла и все приоритеты, имеющие значение 2, меняются на значение 3. Сделано это для того чтобы предотвратить влияние предыдущих циклов при возникновении тупиков.

Таким образом, этот приоритет не позволяет побывать фишке-ресурсу в одной позиции более одного раза, за исключением того случая, когда фишка будет возвращаться из тупика. Также найденная цепь будет повторяться максимальное количество раз.

Приоритетом третьего уровня будет обычный статический (не меняющийся в результате всей работы сети) приоритет. Данный приоритет будет давать предпочтение согласованным переходам перед несогласованными переходами. После запуска сети наступает такой момент, когда ни один переход не может сработать. Одним переходам это не позволяет сделать отсутствие входных фишек, другим – нулевые приоритеты, при этом появится сообщение об отсутствии рабочих переходов. Сеть зайдет в тупик. Количество фишек в стоке будет искомым значением максимального потока.

Задача в нашем примере при использовании динамических приоритетов решается в среднем за 27 шагов.

Выводы

Проведена успешная попытка моделирования сетями Петри решения задачи о максимальном потоке. Реализован классический алгоритм Форда-Фалкерсона. Введены обобщения сетей Петри – сети с динамическими приоритетами. Подобный подход имеет хорошие перспективы для моделирования практических задач.