При автоматизированном проектировании элементов, узлов и устройств технических объектов разработчики встречаются с проблемой малых выборок, т.е. отсутствия необходимого количества эмпирических данных для принятия рационального конструктивно-технологического решения [1].
Для «обхода» проблемы малых выборок при оценивании плотностей вероятностей p(x) увеличим объем исходных данных xi, i = 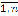 , за счет результатов статического моделирования. С этой целью в β-окрестности каждой i-й точки выборки осуществим m имитаций с законом распределения p2(x). Полученная статическая выборка xi + xj2, j =
, за счет результатов статического моделирования. С этой целью в β-окрестности каждой i-й точки выборки осуществим m имитаций с законом распределения p2(x). Полученная статическая выборка xi + xj2, j = 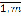 , i =
, i = 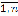 , при равновероятных значениях xi, i =
, при равновероятных значениях xi, i = 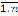 ,соответствует смеси плотностей вероятностей:
,соответствует смеси плотностей вероятностей:
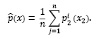 (1)
(1)
Нетрудно заметить, что непараметрическая оценка (1) имеет вид
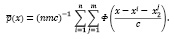 (2)
(2)
Существующий парадокс традиционных методов идентификации стохастических моделей состоит в сопоставлении конечной случайной выборки наблюдений переменных изучаемых объектов с конкретным набором параметров модели, оптимальном в некотором смысле. Предлагается рандомизированный подход определения коэффициентов размытости непараметрических решающих правил на основе процедуры их случайного выбора, который рассматривается на примере оптимизации алгоритмов формирования литографических процессов.
Впервые методика случайного выбора коэффициентов размытости ядерных функций при синтезе непараметрической оценки плотности вероятности была предложена в 1975 г. Т. Вагнером [1]. Формирование случайной последовательности коэффициентов размытости при оценивании плотности вероятности p(x) осуществляется на основе выборки расстояний между исходными наблюдениями (xi, i = 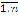 ) и их k-ближайшими соседями.
) и их k-ближайшими соседями.
Рассмотрим рандомизированный метод оптимизации. Пусть 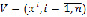 – выборка из n статистически независимых наблюдателей случайной величины
– выборка из n статистически независимых наблюдателей случайной величины 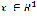 с плотностью вероятности p(x), вид которой неизвестен. Будем считать, что p(x) ограничена и непрерывна со всеми своими производными до второго порядка включительно. В качестве приближения по эмпирическим данным V искомой плотности вероятности p(x) примем статистику типа Розенблатта – Парзена [2]
с плотностью вероятности p(x), вид которой неизвестен. Будем считать, что p(x) ограничена и непрерывна со всеми своими производными до второго порядка включительно. В качестве приближения по эмпирическим данным V искомой плотности вероятности p(x) примем статистику типа Розенблатта – Парзена [2]
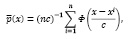 (3)
(3)
где 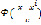 – ядерные функции, удовлетворяющие условиям положительности, симметричности и нормированности;
– ядерные функции, удовлетворяющие условиям положительности, симметричности и нормированности; 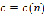 – последовательность положительных чисел (коэффициентов размытости) таких, что
– последовательность положительных чисел (коэффициентов размытости) таких, что
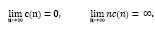 (4)
(4)
Свойства непараметрической оценки плотности вероятности (3), такие как асимптотическая несмещенность, состоятельность, сходимость почти наверное к 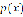 , подробно рассмотрены в работе [3].
, подробно рассмотрены в работе [3].
Для сравнения традиционного и рандомизированного метода оптимизации непараметрической оценки плотности вероятности определим отношение 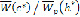 соответствующих им асимптотических выражений среднеквадратических критериев при оптимальных параметрах с и h.
соответствующих им асимптотических выражений среднеквадратических критериев при оптимальных параметрах с и h.
Из условия минимума 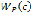 и
и 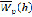 по с и h нетрудно получить
по с и h нетрудно получить
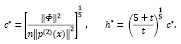 (5)
(5)
При оптимальных параметрах 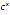 ,
, 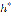 отношение
отношение
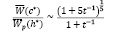 (6)
(6)
меньше единицы при конкретных значениях параметра  закона распределения
закона распределения 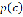 коэффициентов размытия ядерных функций.
коэффициентов размытия ядерных функций.
Однако использование непараметрической оценки со случайными значениями коэффициентов размытия ядерных функций
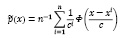 (7)
(7)
позволяет снизить смещение при оценивании плотности вероятностей по сравнению с традиционной статистикой типа (3).
Можно показать, что асимптотическое выражение смещения
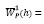
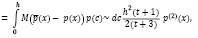 (8)
(8)
а его отношение к соответствующему смещению 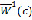 для традиционной непараметрической оценки при оптимальных параметрах
для традиционной непараметрической оценки при оптимальных параметрах 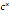 и
и 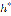
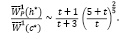 (9)
(9)
Если параметр t плотности вероятности 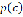 больше или равен 2, то отношение (9) меньше единицы.
больше или равен 2, то отношение (9) меньше единицы.
Анализ выражений (5), (8) показывает, что непараметрическая оценка плотности вероятности со случайными значениями коэффициентов размытости (7) обладает свойствами асимптотической несмещенности и состоятельности. Она характеризуется пониженным смещением (9) и несколько большим значением среднеквадратического отклонения (6) по сравнению с непараметрической статистикой (3). Следует ожидать проявления потенциальной эффективности непараметрической оценки плотности вероятности (7) при конечных объемах статистических данных.
Реализация «обхода» проблем малых выборок при оценивании плотностей вероятностей p(x) обеспечивается также не только увеличением объема исходных данных xi, i = 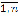 , но и результатами технического моделирования, т.к. сложность и многообразие процессов функционирования проектируемых технических систем, таких как, к примеру, литографическое оборудование, не всегда позволяют получать для них адекватные математические модели, сформулированные в виде различных аналитических соотношений [4].
, но и результатами технического моделирования, т.к. сложность и многообразие процессов функционирования проектируемых технических систем, таких как, к примеру, литографическое оборудование, не всегда позволяют получать для них адекватные математические модели, сформулированные в виде различных аналитических соотношений [4].
Рассмотрим применение метода Лапласа в асимптотической оценке применяемых ядер в результате статистического моделирования [5].
Методом Лапласа можно назвать ту совокупность приемов, способов оценок интегралов 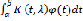 , когда с ростом параметра λ к положительной бесконечности (
, когда с ростом параметра λ к положительной бесконечности (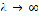 ), график по t ядра
), график по t ядра 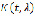 приобретает все более ярко выраженный вид профиля горной страны. Чем больше
приобретает все более ярко выраженный вид профиля горной страны. Чем больше 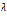 , тем выше (относительно) становятся «пики», глубже и шире (относительно) долины, круче склоны пиков. Не исключается случай, когда с изменением
, тем выше (относительно) становятся «пики», глубже и шире (относительно) долины, круче склоны пиков. Не исключается случай, когда с изменением 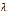 положение «пиков» меняется. К обобщениям метода Лапласа можно отнести приемы оценки интегралов
положение «пиков» меняется. К обобщениям метода Лапласа можно отнести приемы оценки интегралов 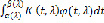 с описанным выше характером ядра
с описанным выше характером ядра 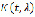 . На рис. 1 представлено несколько примеров таких ядер [6].
. На рис. 1 представлено несколько примеров таких ядер [6].
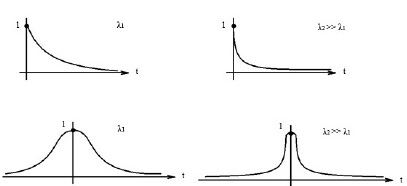
Рис. 1. Графическое отображение ядер
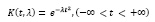 (10)
(10)
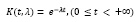 (11)
(11)
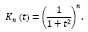 (12)
(12)
Здесь 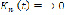 на
на 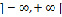 . Введем масштаб 1:2, то есть положим
. Введем масштаб 1:2, то есть положим 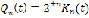 . Графики
. Графики 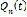 имеют при
имеют при 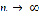 ,
, 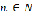 характер, изображенный на рис. 2.
характер, изображенный на рис. 2.
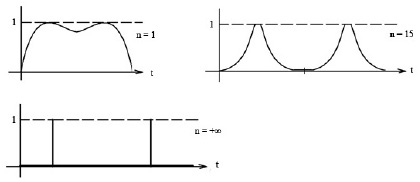
Рис. 2. Графическое отображение специальных ядер
Как уже неоднократно говорилось, содержание метода Лапласа богаче любого количества посвященных этому методу теорем. Можно представить себе ситуацию, когда с ростом 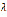 .
.
Растет и количество сравниваемых по величине пиков; когда с ростом 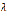 один или несколько пиков «наезжают» на особую точку функции
один или несколько пиков «наезжают» на особую точку функции 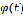 , или вообще любую комбинацию «неприятностей» подобного рода – особенно, если рассматривается интеграл вида
, или вообще любую комбинацию «неприятностей» подобного рода – особенно, если рассматривается интеграл вида 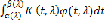 . Поэтому основная трудность здесь не в доказательстве теоремы, а, пожалуй, в отборе тех результатов, которые следует явно сформулировать [6].
. Поэтому основная трудность здесь не в доказательстве теоремы, а, пожалуй, в отборе тех результатов, которые следует явно сформулировать [6].
Естественно рассмотреть вначале случай одного фиксированного пика фиксированной высоты. Полезно различать две возможности:
а) основание пика (то есть узел асимптотики) находится в крайней точке промежутка интегрирования;
б) узел асимптотики лежит внутри промежутка интегрирования.
Представляет интерес еще одно свойство интеграла Лапласа 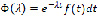 .
.
Пусть этот интеграл сходится при некотором значении 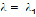 . Тогда он сходится и при всех
. Тогда он сходится и при всех 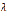 таких, что
таких, что 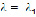 . Нижняя грань
. Нижняя грань 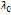 всех
всех 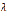 , при которых
, при которых 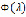 сходится, называется абсциссой сходимости
сходится, называется абсциссой сходимости 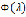 (в отличие от степенных рядов, у интегралов
(в отличие от степенных рядов, у интегралов 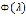 абсциссы сходимости и абсолютной сходимости, в общем случае, различны). В дальнейшем предполагается, что у всех рассматриваемых интегралов Лапласа существует конечная абсцисса сходимости. Следующая вспомогательная лемма позволяет раз и навсегда ограничиться интегралами, распространенными на конечный отрезок.
абсциссы сходимости и абсолютной сходимости, в общем случае, различны). В дальнейшем предполагается, что у всех рассматриваемых интегралов Лапласа существует конечная абсцисса сходимости. Следующая вспомогательная лемма позволяет раз и навсегда ограничиться интегралами, распространенными на конечный отрезок.
Лемма. Пусть функция 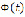 интегрируема на любом промежутке
интегрируема на любом промежутке 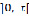 ,
, 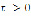 , интеграл
, интеграл
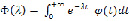
сходится при 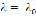 . и
. и 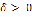 – произвольное положительное число [6].
– произвольное положительное число [6].
Тогда для интеграла
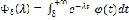
справедлива асимптотическая оценка 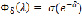 ,
, 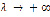 .
.
Доказательство. По условию интеграл
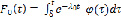
сходится при 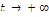 . к некоторому конечному пределу. Также по условию функция
. к некоторому конечному пределу. Также по условию функция 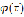 (а с ней и
(а с ней и 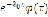 ), локально интегрируема, вследствие чего
), локально интегрируема, вследствие чего 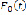 непрерывная функция при
непрерывная функция при 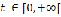 . Непрерывная на
. Непрерывная на 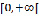 функция, имеющая при
функция, имеющая при 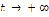 конечный предел, ограничена на
конечный предел, ограничена на 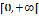 : поэтому существует и конечное число
: поэтому существует и конечное число
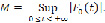
Заметив это, проведем в интеграле 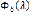 при любом
при любом 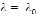 следующие преобразования:
следующие преобразования:
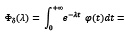
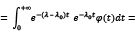
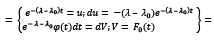
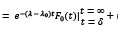
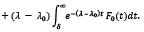
Теперь оценка по модулю дает (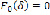 по определению,
по определению, 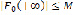 ):
):
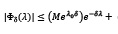
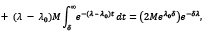
что и требовалось доказать.
Таким образом, любой «хвост» 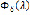 интеграла Лапласа с конечной абсциссой сходимости всегда экспоненциально мал. Поэтому с точки зрения асимптотических оценок можно ограничиться любым конечным промежутком
интеграла Лапласа с конечной абсциссой сходимости всегда экспоненциально мал. Поэтому с точки зрения асимптотических оценок можно ограничиться любым конечным промежутком 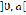 ,
, 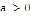 . Кроме того, эта асимптотика определяется лишь поведением функции
. Кроме того, эта асимптотика определяется лишь поведением функции 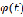 при
при 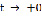 .
.
Предложена математическая модель непараметрической оценки плотности вероятности в условиях малых выборок и метод Лапласа в асимптотической оценке применяемых ядер обеспечивают возможность технического моделирования, без использования реальных технологических процессов и дорогостоящего оборудования. Реализация «обхода» проблем малых выборок обеспечивает увеличение объема исходных данных и повышает эффективность технического моделирования [7].

