Введение
На данный момент в мире существует множество алгоритмов, обеспечивающих различные уровни криптографической стойкости, основанные на различных принципах защиты, от применения секретных алгоритмов (морально устаревшие методы), до использования математических методов, основанных на вычислительной сложности. Одно из современных перспективных направлений криптографической защиты информации в распределенных компьютерных сетях есть применение алгоритмов, основанных на поведенческих свойствах нелинейных динамических систем, так называемых «детерминированном хаосе».
Цель: исследовать и разработать криптографический алгоритм на основе отображения нелинейной динамической системы для шифрования графической информации. Провести исследования данного криптографического алгоритма по всем необходимым параметрам.
Описание алгоритма
При шифровании в основном исследуются телекоммуникационные технологии, основанные на использовании различных способов кодирования матриц. Наряду с использованием сложных регулярных закономерностей для кодирования матриц рассматривалась возможность применения нерегулярных процессов [1]. При этом для перестановки элементов матрицы использован стандартный генератор псевдослучайных чисел.
Наряду с тем, что при применении модели матрицы возможно восстановление потерь «голографическим» методом, в принципе, при перестановке элементов матрицы возможно и вскрытие шифра, хотя в ряде случаев это - очень сложно. В то же время с помощью псевдослучайных генераторов можно получать довольно стойкие криптосистемы, если осуществлять не перестановку элементов матрицы, а изменение цвета элементов, формирующих изображение. При этом в качестве генераторов псевдослучайных сигналов, как представляется, весьма подходят генераторы с хаотической динамикой, и особенно искусственно сконструированные. Они предпочтительнее тем, что хаос, описываемый их уравнениями (при относительной простоте записи) может быть более развитым.
Рассматривается новый способ шифрования информации, основанный на хаотическом изменении цвета символов, формирующих изображение. Для генерирования псевдослучайной последовательности чисел используется одномерное отображение [2,3]. Особенностью системы, обладающей хаотической динамикой является высокая чувствительность к изменению параметров. Именно это затрудняет несанкционированное дешифрование при использовании для кодирования информации детерминированного хаоса.
Использование хаотических решений рассмотренного отображения позволяет создать достаточно сложный шифр, который не поддается раскрытию, если не воспроизведены точные значения начальных условий и параметров динамической системы, при которых выполнялось ее решение.
Подмешивание псевдослучайной последовательности чисел, получаемой на основе решения хаотического отображения, целесообразно осуществлять так, чтобы происходило хаотическое изменение их палитры цвета. Это является основой разработанной программы, обеспечивающей шифрование и дешифрование с использованием системы с хаотической динамикой.
Преобразование графической матрицы осуществляется путем присвоения каждому символу, формирующему изображение, нового цвета в соответствии не только с хаотическими решениями рассматриваемого отображения, но и с его исходной палитрой цвета. В этом случае выполняется условие, при котором индекс нового цвета пикселя равен исходному индексу цвета пикселя плюс дополнительный индекс цвета пикселя, определяемый решением хаотического отображения. При этом каждый символ графической матрицы последовательно преобразуется в одном и том же стековом блоке памяти. При дешифровании используется аналогичный алгоритм преобразований. Отличие заключается лишь в том, что при формировании палитры цвета осуществляется вычитание псевдослучайной последовательности чисел, формируемых на основе решений тех уравнений, которые использовались при шифровании.
Таким образом, алгоритм шифрования графического объекта будет состоять из следующих шагов:
1) Сопоставление пикселю графического изображения трех координат r, g, b (эти числа составляют RGB-код пикселя);
2) Задание начальных условий (параметров) динамической системы;
3) На основе решения нелинейного отображения с хаотической динамикой – генерация последовательности значений псевдослучайных чисел h;
4) Определение индексов нового цвета пикселя
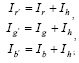
5) Получение нового (абсолютно другого) цвета пикселя;
6) Выполнение шагов 1-5 для всех элементов многоцветной матрицы.
Как уже говорилось выше, для дешифрования используется аналогичный алгоритм преобразований:
1) Получение трех координат r’, g’, b’ пикселя зашифрованного графического изображения;
2) Задание начальных условий (параметров) динамической системы;
3) Восстановление последовательности значений псевдослучайных чисел h по известным значениям управляющих параметров;
4) Восстановление значений индексов первоначального цвета пикселя
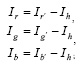
5) Формирование RGB-код пикселя, т.е. восстановление его первоначального цвета;
6) Выполнение шагов 1-5 для всех элементов многоцветной матрицы.
Для иллюстрации процессов шифрования и дешифрования использовалась цветная матрица 24 бита в виде графического изображения (рисунок 1).

Рис. 1. Исходный графический объект
Хотя изображение на рисунке 1 является цветным, оно распечатано на принтере как черно-белое. Поэтому изменение цвета пикселей на этом рисунке отображается тональностью серого. Изображение, представленное на рисунке 1 после процедуры преобразования в зашифрованной матрице принимает вид, иллюстрируемый на рисунке 2. Зашифрованное изображение отображает хорошее (хаотическое) перемешивание цветов (в представленном виде – тональности серого) пикселей, так что исходная информация надежно замаскирована.

Рис. 2а. Изображение рисунка 1 в зашифрованном виде

Рис. 2б. Изображение рисунка 1 при неправильном дешифровании
При шифровании в случае (рисунка 2а) в нелинейном отображении с хаотической динамикой при T=0,8 заданы (для примера) следующие значения варьируемых параметров: α=1,12345671234567, γ=1,3. При санкционированном дешифровании (рисунок 2а), когда параметры α, γ, T введены с абсолютной точностью, исходный графический объект, показанный на рисунке 1 воспроизводится без изменения.
В случае малейших ошибок хотя бы по одному параметру (например, при несанкционированном входе) дешифрование оказывается невозможным, т.к. в результате будет получено изображение, не соответствующее реальному (исходному). Даже при ошибке в определении одного из параметров, составляющей 10-15 вид матрицы остается подобным рисунку, показанному на рисунке 2а, при этом распределение цвета пикселей, естественно иное (рисунок 2б).
Приведенные исследования шифрования и дешифрования свидетельствуют о том, что при кодировании цвета символов, формирующих изображение, могут быть использованы псевдослучайные последовательности целых чисел, являющихся результатом решений нелинейного отображения с хаотической динамикой.
При шифровании с помощью последовательности псевдослучайных чисел, использование изменения цвета пикселов, формирующих изображение, позволяет обеспечить его надежную маскировку. Учитывая устойчивость шифра, информацию, зашифрованную рассмотренным способом можно передавать по открытым сетевым каналам, в том числе и по электронной почте, а также хранить в архивах со свободным доступом. При этом маскировка информации при ее передаче по открытым каналам не хуже, чем ее маскировка при передаче излучаемыми хаотическими колебаниями [4-8].
В качестве тестового выбрано черно-белое изображение размером 100×100 пикселов с 256 градациями серого уровня. Изображение и его спектр приведены на рисунках 3а и 3б соответственно.

Рис. 3а. Тестовое черно-белое изображение с 256 градациями серого уровня
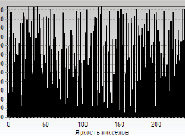
Рис. 3б. Спектр яркости цветов пикселов изображения на рисунке 3а
Первые тесты по применению этого алгоритма для шифрования информации показали его потенциальную пригодность для криптографического кодирования. Во-первых, в шифрованном изображении не присутствует никаких структур (рисунок 4а), и его спектр яркости цветов пикселов стал почти однородным (рисунок 4б).

Рис. 4а. Результат кодирования тестового изображения
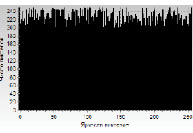
Рис. 4б. Спектр яркости цветов пикселов шифрованного изображения
Во-вторых, предложенная схема чувствительна к малейшим изменениям начальных условий и/или параметров (получаемые при этом шифры абсолютно различны). В-третьих, она малочувствительна к ошибкам в шифртексте, т.е. при расшифровывание искажения в шифртексте сказываются локально, а не распространяются на все изображение.
В заключении нужно отметить, что надежность данного алгоритма шифрования в большей степени зависит от характеристик применяемого метода генерации псевдослучайных чисел, т.к. на одном из начальных этапов шифрования мы вносим изменения в псевдослучайную числовую последовательность.
Вывод
1) Использование хаотического отображения позволяет создать достаточно сложный шифр, который не поддается раскрытию, если не воспроизведены точные значения начальных условий и параметров динамической системы, при которых выполнялось ее решение.
2) Разработанный криптографический алгоритм преобразования текстовой и графической информации базируется на том, что для хаотических динамических систем существуют периодические возмущения, приводящие к стабилизации цикла заданного периода.
3) Информация шифруется с помощью таких стабилизированных циклов. В качестве передаваемого сигнала используются возмущения, а ключом для расшифровки полученного сообщения служит вид отображения.
4) Приведенные исследования кодирования свидетельствуют о том, что при кодировании как текстовой информации, так и цвета символов, формирующих изображение, могут быть использованы псевдослучайные последовательности целых чисел, являющихся результатом решений нелинейного отображения с хаотической динамикой.

