Within the two-body αt-model for 7Li nucleus the relative motion wave functions in 5He + d channel have been built by using the projecting method in the dynamic potential cluster model. It is necessary to note, that in this calculations the {dt} configuration of 5He nucleus has been taken into account. The graphs of obtained 5He + d relative motion wave functions at the various values of the oscillatory parameter of α-particle are presented. S-wave of the relative d5He motion wave function, obtained in this work within the {dt} configuration of 5He nucleus, doesn’t have a node in contrast to the corresponding one obtained earlier within the {αn} configuration of 5He nucleus. Obtained functions have been used for calculation of the spectroscopic Sd-factors of the deuteron separation from 7Li nucleus. Also the comparative analysis of the obtained spectroscopic Sd-factors with corresponding ones calculated earlier within the {αn} configuration of this nucleus has been performed.
In the present work the construction of relative motion wave functions (WF) in 5He + d channel with taking into account dt-configuration of 5He nucleus is performed within the dynamic potential cluster model (DPCM) on the basis of projecting technique described in detail in Refs [1–3]. Below, the main stages of construction of mentioned above WF are presented.
To construct 5He{dt} relative motion WF it is necessary to calculate the overlap integral:
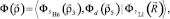(1)
where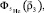 
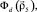
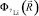are the WF of 5He{dt}, d and 7Li{αt} nuclei, 
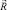is the relative motion coordinate of α and t clusters, 
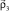is the relative motion coordinate of d and t clusters, 
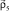is the np relative motion coordinate, 
is the relative motion coordinate of 5He and d nuclei. The integration with respect to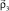 
and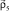 
leads to the corresponding 5He{dt} relative motion WF as a function of 
variable.
Next, let us comment the model functions used in calculations. For description of 7Li{αt} nucleus state the following WF is used:
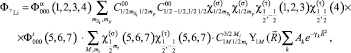(2)
where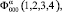 
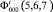are the internal WF of α-particle and tritium correspondingly,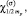 
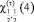are the spin and isospin functions of proton,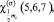 
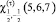are the spin and isospin functions of tritium, 
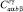are the Clebsch-Gordan coefficients, 
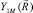is the angular spherical function.
It is obvious that in this case the projecting of 7Li{αt} nucleus WF on 5He + d channel affects the internal structure of α-particle, so for our calculation the WF of α-particle is also needed:
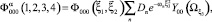(3)
where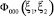 
is the internal function of tritium being in the α-particle structure, which has been obtained in Refs [4, 5] within the resonating group method (RGM).
The state of tritium in 7Li{αt} structure is described by WF:
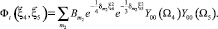(4)
The WF of 5He{dt} nucleus with the total momentum j and its projection mj may be formally presented in the form:
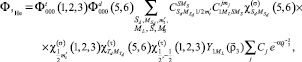(5)
where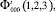 
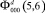are the internal WF of tritium and deuteron in 5He{dt} structure correspondingly.
The state of deuteron is described by the following WF:
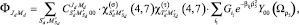(6)
where Jd, Md are the total angular momentum and its projection.
To calculate integral (1) it is necessary to perform the direct transformations of relative Jacobi coordinates at the transition from 7Li{αt} system to d + 5He{dt} system, i.e.
,
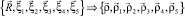and, similarly, back transformations. It is fairly easy to do, so we shall not give these transformations explicitly.
Next, using the projection technique presented in [1–3], we obtain the final form of the clusters relative motion wave function in the channel:
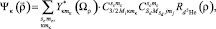(7)
where κ, mκ are the orbital momentum of d5He relative motion and its projection, sc, mc are 5He{dt} + d channel spin and its projection,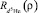 
is the radial part of the relative motion WF which has the form:
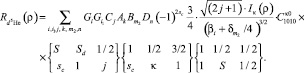(8)
In expression (8) the integral Iκ(ρ) at κ = 0 (S-component) has the following form:
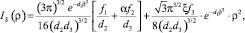(9)
and at the value κ = 2 (D-component) it takes the form:
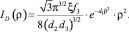(10)
The obtained relative motion WF in 5He{dt} + d channel (7) are plotted in Fig. 1 and 2 at the various values of the oscillatory parameter of α-particle. As it seen from Fig. 1, S-wave of the relative d5He motion WF, obtained in this work within the {dt} configuration of 5He nucleus, doesn’t have a node in contrast to the corresponding one obtained earlier within the {αn} configuration of 5He nucleus [6].
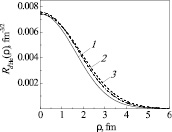
Fig. 1. Relative motion wave functions in 5He{dt} + d channel (S-wave), obtained at the various values of the oscillatory parameter r0 of α-particle: 1 – r0 = 1,7 fm; 2 – r0 = 2 fm; 3 – r0 = 2,2 fm
a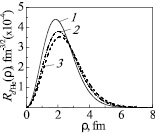
b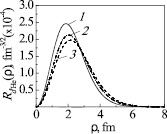 
Fig. 2. Relative motion wave functions in 5He{dt} + d channel: D1/2 – wave (a) and D3/2 – wave (b). Curve denotations are the same as in Fig. 1
On the basis of formula (7) it is easy to obtain the formula for calculation of the spectroscopic Sd-factors of the separation of deuterons from 7Li nucleus:
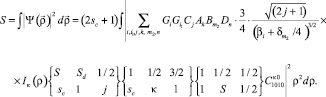(11)
The results of theoretical calculations of the spectroscopic Sd-factors in 5He{dt} + d channel are presented in Table.
It is necessary to note that presented in Table values of the spectroscopic Sd-factors for 5He{dt} + d channel, obtained with taking into account {dt} configuration of 5He nucleus, are very small in comparison with the values obtained earlier for 5He{αn} + d channel in Refs. [7, 8]. As it seen in the present calculations S-wave is dominating, and weight of D-wave is about ~1 %. Apparently, this situation is due to the fact that 5He nucleus in the ground state exists only in {αn} configuration. {dt} configuration of this nucleus is more probable only in the first excited state of 5He nucleus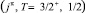 
[9]. Thus, in future it would be urgent to calculate the spectroscopic Sd-factors for 
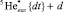channel, when 5He{dt} nucleus is in the first excited state.
The results of calculations of the spectroscopic Sd-factors for 5He{dt} + d channel, depending on the oscillatory parameter r0 of α-particle
|
r0, fm |
S0 |
S2 |
РS, % |
РD, % |
|
1,7 |
4,01∙10–4 |
4,84∙10–6 |
98,8 |
1,2 |
|
2,0 |
5,23∙10–4 |
4,70∙10–6 |
99,1 |
0,9 |
|
2,2 |
5,89∙10–4 |
4,71∙10–6 |
99,2 |
0,8 |
The work is submitted to the International Scientific Conference «Implementation of integrated model of educational institutions, implements educational programs different levels of education», Republic of Singapore, December, 10-17, 2013, came to the editorial office оn 18.11.2013.