При современном уровне развития компьютерной техники, а также аналитических и численных методов решения инженерных задач появляется возможность моделирования таких сложных процессов, как термодеформационные процессы и процессы структурных превращений при сварке и сопутствующих операциях: термической и механической обработке, а также последующих эксплуатационных нагружениях.
Принципиальным вопросом при моделировании сварки является представление процесса ввода сварочной теплоты в металл [1, 2, 4]. При решении этой задачи можно выделить два подхода. В первом источником теплоты служит объем наплавляемого металла или сварочная ванна. Второй подход опирается на разработку и использование моделей сварочных источников, описывающих поверхностное или объемное распределение тепловой мощности, передаваемой от источника сварочного нагрева к металлу.
Наиболее точную картину ввода и последующего перераспределения теплоты при сварке дают трехмерные модели источников, специально разработанные для конкретных видов сварки на основе экспериментальных и расчетных данных.
Решение объемной задачи о нахождении температурных полей при воздействии сварочного источника тепла на металлическую пластину при сварке встык необходимо для получения исходных данных для нахождения таких опасных сопутствующих факторов сварки, как временные и остаточные объемные напряжения и деформации.
В расчете используется метод конечных элементов (МКЭ), реализованный в программно-методическом комплексе ANSYS. Этот общецелевой программный продукт позволяет моделировать объекты проектирования различных физических полей. Для перехода от решения тепловой задачи к решению механической задачи используется возможность связи нескольких физических полей. Выбран последовательный метод связи полей. Его алгоритм в нашем случае следующий:
1. На первом этапе при помощи объемного термического элемента SOLID70 пошагово решается температурная задача – этапы нагрева и остывания, результаты узловых решений сохраняются в файл температурных результатов FILE.RTH;
2. На следующем этапе необходимо сменить тип элемента на соответствующий объемный прочностной конечный элемент первого порядка с механическими свойствами – SOLID45, а также необходимо задать граничные условия;
3. На заключительном этапе решается нестационарная термоупругопластическая задача, исходные данные для которой на каждом шаге извлекаются из файла результатов температурного решения и применяются к структурной дискретной модели.
Решение трехмерной задачи с нагревом при помощи движущегося распределенного источника тепла позволит провести анализ поперечных, продольных и касательных остаточных и временных напряжений и деформаций, а также напряжений и деформаций по толщине образца. Полезным применением полученной модели является возможность исследования различных воздействий, например, механических для устранения остаточных напряжений и деформаций.
При решении объемной температурной задачи потребуется восьми узловой трехмерный конечный элемент SOLID70. У него имеется одна степень свободы – температура (TEMP). Он может принимать нагрузку в виде теплового потока. Результатом решения является множество узловых данных, состоящее из тепловых напряжений и температуры по всему объему исследуемой пластины.
Рассматриваются два этапа решения тепловой задачи:
1) сварочный цикл, на котором моделируется приложение распределенного теплового потока от движущегося источника тепла и нагрев шовной и околошовной зоны до температуры разупрочнения стали;
2) цикл остывания после сварки, во время которого моделируется остывание образца до комнатной температуры (+15°С).
Построим модель металлической пластины (рис.1) размером 260х62х19мм. С одного торца применим условие адиабатического теплообмена (тепловая симметрия – отсутствие перехода тепла через данную плоскость).

Рис. 1. Дискретная модель объекта
Размер конечного элемента принимается 1/5 от толщины пластины на основании ряда опытов, которые показали удовлетворительную сходимость при таком способе разбиения на конечные элементы, как в тепловой, так и в прочностной задаче.
Исходные данные: мощность сварочного источника на выходе: Q=4,6 КВт, КПД Nu=0,7. Далее описывается теоретическая часть первой стадии решения.
Нагрузка прикладывается в виде теплового потока, распределенного по нормальному закону распределения, к верхней поверхности пластины.
Q=I•U. (1)
В виду симметричности модели, найдем, что количество тепла, прикладываемое к исследуемой половине равно:
Q=I•U/2. (2)
Принимая КПД равным 0.7, получим:
q=Nu•Q. (3)
Тепловой поток распределен по нормальному закону, с максимальным значением в центре сварочной ванны. Согласно [3] формула распределения теплового потока по поверхности полубесконечной пластины при сварке встык находится по формуле:
q2=q2me-kr , (4)
где q2 – поток в любой точке, q2m – максимальное значение в центре сварочной ванны, k – коэффициент концентрации теплового потока, r – расстояние от центра сварочной ванны.
Тогда применительно к условиям задачи можно составить закон приложения теплового потока:
q2m=qk/π, (5)
где k=1/3.
Выведем зависимость q(x,y), на языке APDL для ввода в ANSYS:
q(X,Y)=q2m • exp(-k • sqrt((X0-X) • (X0-X) + (Y0-Y) • (Y0-Y))), (6)
где X,Y – любая (скользящая) координата на поверхности пластины, X0, Y0 – координаты центра приложения нагрузки (текущего центра сварочной ванны).
После прохождения сварочного источника вдоль сварного шва получим температурные поля, показанные на рисунке 2.
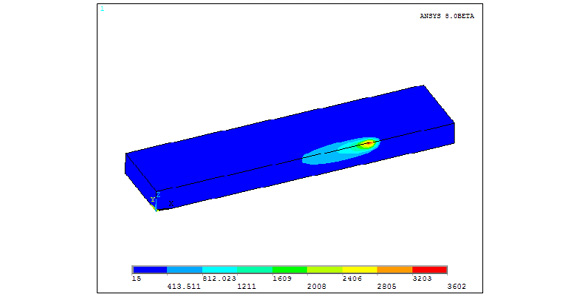
Рис. 2. Температурные поля после прохода сварочного источника тепла
После применения тепловой нагрузки (моделирования сварки), необходимо исследовать процесс остывания заготовки. Для этого на втором этапе используется экспоненциальный закон изменения шага времени:
Ti=0.5×ei/10. (7)
При дальнейшем решении задачи накапливаются данные о тепловых нагрузках, которые возникают в пластине, остывающей в условиях естественной конвекции.
Анализ полученных данных позволяет обнаружить следующие особенности:
1) распределение температуры является «кометообразным»;
2) расчетная область расплавления металла повторяет форму очертаний сварочной ванны;
После накопления всех данных возможно решение полной термомеханической задачи. В результате решения будут выявлены объемные временные и остаточные сварочные напряжения и деформации (рисунки 3-5).
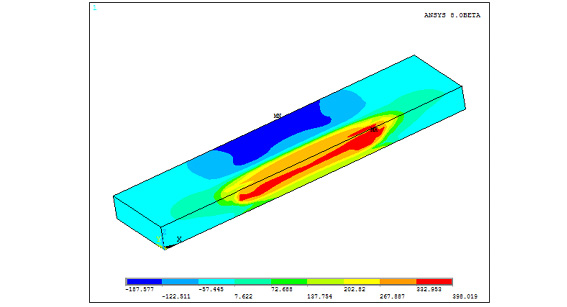
Рис. 3. Временные эквивалентные напряжения
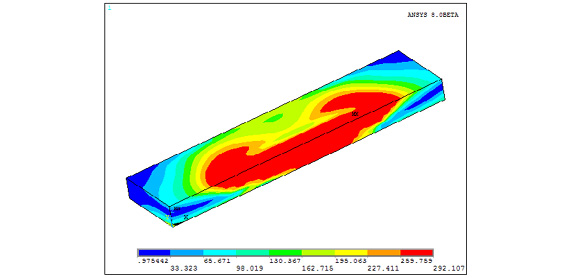
Рис. 4. Остаточные эквивалентные напряжения
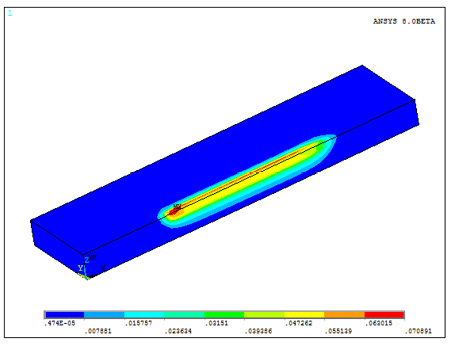
Рис. 5. Остаточные эквивалентные деформации
Полученные результаты по значению остаточных напряжений и деформаций адекватно сопоставимы с экспериментальными лабораторными измерениями [3]. Для того, чтобы продемонстрировать возможности, которые может дать исследование на основе компьютерной модели решим задачу по снижению остаточных продольных напряжений при помощи механического воздействия. Применим к торцам пластины растягивающую нагрузку в размере 0,6 от предела текучести данного вида стали, а затем снимем ее. Продольные напряжения до механического воздействия показаны на рисунке 6. Остаточные продольные напряжения снизились на 40%.
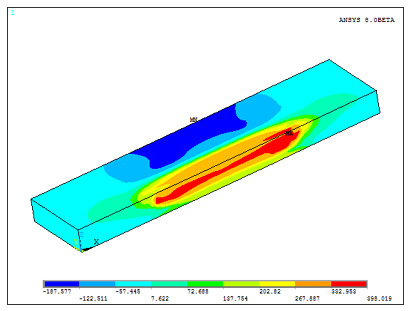
Рис. 6. Остаточные продольные напряжения до воздействия
Полученная компьютерная модель позволяет подробно проанализировать воздействие любых воздействий (температурных, механических) на все компоненты напряжений и деформации. За счет чего становится возможным целенаправленное создание комплексной методики по устранению опасных остаточных факторов после сварки.
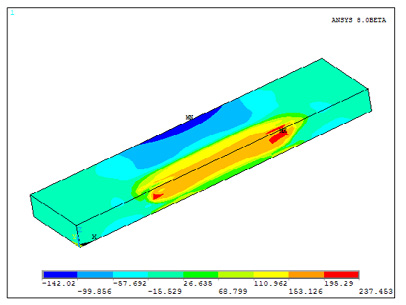
Рис. 7. Остаточные продольные напряжения после воздействия

