Пусть 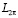 – класс 2 π-периодических суммируемых на
– класс 2 π-периодических суммируемых на 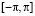 функций, С2π – класс 2 π-периодических непрерывных функций,
функций, С2π – класс 2 π-периодических непрерывных функций, 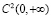 – класс функций, обладающих непрерывными на
– класс функций, обладающих непрерывными на 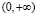 вторыми производными. В настоящей работе рассматриваются экспоненциальные средние
вторыми производными. В настоящей работе рассматриваются экспоненциальные средние
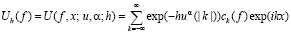 (1.1)
(1.1)
рядов Фурье функций 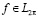 . В определении (1.1)
. В определении (1.1)
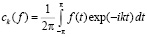 , (1.2)
, (1.2)
– коэффициенты Фурье функции f,  – произвольный фиксированный параметр, функция
– произвольный фиксированный параметр, функция 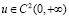 принимает положительные значения,
принимает положительные значения, 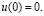
Одна из основных задач, рассматриваемых в настоящей работе – изучение поведения семейства операторов 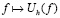 при
при 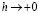 . А именно, мы будем изучать сходимость (1.1) в точках Лебега, т.е. в точках х, обладающих свойством
. А именно, мы будем изучать сходимость (1.1) в точках Лебега, т.е. в точках х, обладающих свойством
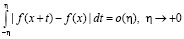 .
.
Точки Лебега, как известно ([1], с. 111 ), расположены почти всюду для каждой  .
.
Частными случаями (1.1) являются
1) решение
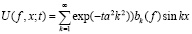
задачи теплопроводности
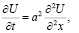
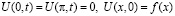
в стержне длины π с постоянным коэффициентом температуропроводности a2 (t>0 – время протекания процесса, 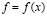 – заданное распределение начальных температур,
– заданное распределение начальных температур, 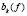 – синус-коэффициенты Фурье функции f );
– синус-коэффициенты Фурье функции f );
2) решение
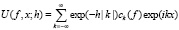 (1.3)
(1.3)
задачи Дирихле
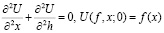
в полуплоскости (нахождение стационарного распределения температур в точках  с заданной на границе
с заданной на границе 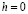 температурой
температурой 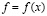 ). Операторы, определяемые соотношением (1.3) известны как средние Пуассона-Абеля ([1], с. 160-165) и играют значительную роль в различных вопросах анализа. Однако, не до конца изучено ([2]) даже наиболее простое и естественное обобщение
). Операторы, определяемые соотношением (1.3) известны как средние Пуассона-Абеля ([1], с. 160-165) и играют значительную роль в различных вопросах анализа. Однако, не до конца изучено ([2]) даже наиболее простое и естественное обобщение
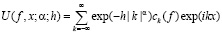 (1.4)
(1.4)
средних (1.3) на случай любого 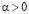 . Речь идет, в частности, об (1.4) как решении обобщенной задачи Дирихле в полуплоскости
. Речь идет, в частности, об (1.4) как решении обобщенной задачи Дирихле в полуплоскости
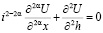 ,
,
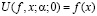 , (1.5)
, (1.5)
где дифференцирование по х есть соответствующее дробное дифференцирование, а (1.5) понимается как предельное соотношение
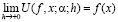 (1.6)
(1.6)
(характер сходимости обсуждается ниже).
2. Основной результат
Теорема 2.1.
Пусть 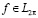 и при каждом h>0
и при каждом h>0
 . (1.7)
. (1.7)
1) Если 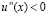 при всех
при всех 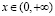 и
и 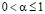 , то соотношение
, то соотношение
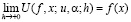 (1.8)
(1.8)
имеет место в каждой точке Лебега функции f и равномерно по х для всякой f∈ С2p.
2) Результат (1.8) сохраняется для 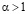 , если (в дополнение к (1.7) ) существует постоянная
, если (в дополнение к (1.7) ) существует постоянная 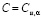 , такая, что при всех
, такая, что при всех 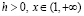
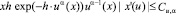 , (1.9)
, (1.9)
и функция
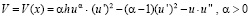 (1.10)
(1.10)
имеет на  конечное число нулей.
конечное число нулей.
3. Вспомогательные утверждения. Рассмотрим бесконечную произвольную последовательность
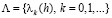 , (2.1)
, (2.1)
определяемую значениями параметра h>0, и соответствующее семейство линейных средних ряда Фурье произвольной f∈ L2π
 .
.
Последовательность (2.1) называется выпуклой (вогнутой), если
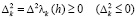 ,
,
где 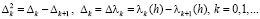
Последовательность (2.1) кусочно-выпукла, если 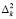 меняет свой знак конечное число раз,
меняет свой знак конечное число раз, 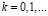 Поведение линейных средних рядов Фурье, определяемых выпуклыми конечными последовательности изучались в работе С.М. Никольского [3]. В следующем утверждении (имеющем и самостоятельный интерес) некоторые результаты [3] распространяются на «полунепрерывный» случай (2.1).
Поведение линейных средних рядов Фурье, определяемых выпуклыми конечными последовательности изучались в работе С.М. Никольского [3]. В следующем утверждении (имеющем и самостоятельный интерес) некоторые результаты [3] распространяются на «полунепрерывный» случай (2.1).
Лемма 2.1. Пусть последовательность (2.1) выпукла (вогнута) и при каждом 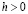 ее члены удовлетворяют условиям
ее члены удовлетворяют условиям
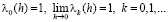 (2.2)
(2.2)
и
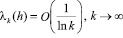 . (2.3)
. (2.3)
Тогда соотношение
 (2.4)
(2.4)
имеет место в каждой точке Лебега функции f и равномерно по х для всякой f∈С2p.
Утверждение сохраняется, если последовательность (2.1) кусочно-выпукла, выполнено условие (2.3) и существует постоянная C (зависящая лишь от λ) такая, что при всех 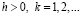
|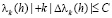 . (2.5)
. (2.5)
Доказательство. Пусть
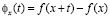 .
.
Воспользовавшись интегральной формой (1.1) коэффициентов Фурье и преобразованием Абеля ([1], c.15), запишем
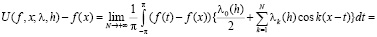
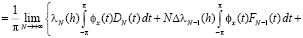
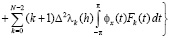 , (2.6)
, (2.6)
где
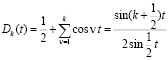 и
и 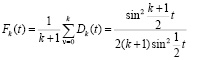
– соответственно, ядро Дирихле и ядро Фейера ([1], с.86, 148). Согласно классическим результатам ([1], с.113, 151) для любого 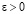 в каждой точке Лебега имеют место соотношения
в каждой точке Лебега имеют место соотношения
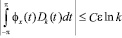 и
и 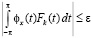
при всех значениях k, больших некоторого 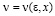 ; постоянная С в первом из неравенств не зависит от k. Учитывая (2.3), очевидные оценки
; постоянная С в первом из неравенств не зависит от k. Учитывая (2.3), очевидные оценки 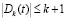 и
и 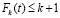 и считая, что
и считая, что 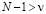 в (2.5), получим теперь, что модуль выражения, записанного под знаком предела в (2.6), не превосходит суммы
в (2.5), получим теперь, что модуль выражения, записанного под знаком предела в (2.6), не превосходит суммы
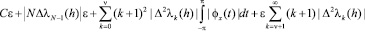 . (2.7)
. (2.7)
Далее, согласно (2.2), 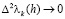 при
при 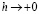 и
и 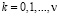 . Кроме того, для выпуклой последовательности при каждом
. Кроме того, для выпуклой последовательности при каждом  имеют место соотношения ([1], с. 155-156)
имеют место соотношения ([1], с. 155-156)
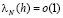 ,
, 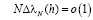 при
при 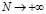 (2.8)
(2.8)
и (в силу преобразования Абеля)
 ; (2.9)
; (2.9)
в (2.8) т и п – любые натуральные числа, причем m<n
В частности, согласно (2.9), (2.3) и (2.8)
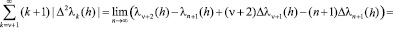
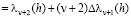 ,
,
и теперь из (2.6) вытекает, что
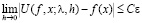 .
.
Отсюда, ввиду произвольности ε, и следует выполнимость соотношения (2.4) в каждой точке Лебега.
Далее, согласно преобразованиям типа (2.6) и соотношениям (2.3), (2.8), (2.9) для нормы 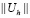 каждого из операторов
каждого из операторов 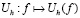 , действующего из С2p в С2p справедлива оценка
, действующего из С2p в С2p справедлива оценка
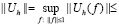
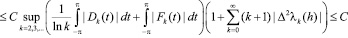 ,
,
где постоянная С зависит лишь от l. Следовательно, равномерная по х сходимость (2.4) имеет место в силу теоремы Банаха-Штейнгауза.
Если же последовательность L кусочно-выпукла, так что 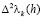 сохраняет свой знак при
сохраняет свой знак при 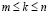 для некоторых натуральных m и n, то сумма
для некоторых натуральных m и n, то сумма 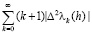 равна конечному числу (числу перемен знаков последовательности
равна конечному числу (числу перемен знаков последовательности 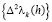 ) блоков-слагаемых, каждый из которых имеет вид (2.9); преобразование суммы (2.9) с
) блоков-слагаемых, каждый из которых имеет вид (2.9); преобразование суммы (2.9) с 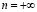 предполагает использование соотношения (2.8). Остается применить к полученным слагаемым оценку (2.5) и повторить рассуждения, использованные в случае выпуклой (вогнутой) последовательности (2.1). Лемма полностью доказана.
предполагает использование соотношения (2.8). Остается применить к полученным слагаемым оценку (2.5) и повторить рассуждения, использованные в случае выпуклой (вогнутой) последовательности (2.1). Лемма полностью доказана.
4. Доказательство теоремы 2.1. Пусть теперь
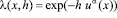 ,
, 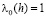 ,
, 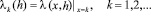 (4.1)
(4.1)
В этом случае, согласно (4.1),
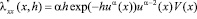 , (4.2)
, (4.2)
где 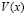 определена соотношением (1.10).
определена соотношением (1.10).
Если 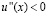 и
и  , то согласно (4.2), последовательность (4.1), оказывается выпуклой, а значит, к ней применима лемма 3.1; при этом условие (2.3) выполнено в виде (1.7). Первая часть теоремы 2.1 доказана.
, то согласно (4.2), последовательность (4.1), оказывается выпуклой, а значит, к ней применима лемма 3.1; при этом условие (2.3) выполнено в виде (1.7). Первая часть теоремы 2.1 доказана.
Для доказательства второй части заметим, прежде всего, что сформулированное условие на функцию V(x) в (1.10) обеспечивают кусочную выпуклость последовательности (4.1). Действительно, пусть, например, V(x) знакопостоянна при 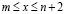 (т и п – некоторые неотрицательные целые числа). Применим к
(т и п – некоторые неотрицательные целые числа). Применим к 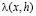 , как функции от х, дважды теорему Лагранжа: первый раз на отрезке [k, k+1], так что
, как функции от х, дважды теорему Лагранжа: первый раз на отрезке [k, k+1], так что
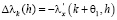 , (4.3)
, (4.3)
а второй раз на отрезке  :
:
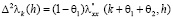 , (4.4)
, (4.4)
где 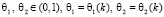 . При
. При 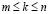 будем иметь
будем иметь 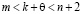 , где
, где 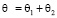 а значит, вторые разности (4.4) в сумме вида (2.9) будут знакопостоянными. Поскольку число интервалов с целочисленными концами, на которых V(x) знакопостоянна, является конечным, то и
а значит, вторые разности (4.4) в сумме вида (2.9) будут знакопостоянными. Поскольку число интервалов с целочисленными концами, на которых V(x) знакопостоянна, является конечным, то и 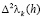 имеет конечное число перемен знака. Условие же (1.9) является достаточным (см. (4.3)) для выполнимости соотношения (2.5). Этим и заканчивается доказательство теоремы 2.1.
имеет конечное число перемен знака. Условие же (1.9) является достаточным (см. (4.3)) для выполнимости соотношения (2.5). Этим и заканчивается доказательство теоремы 2.1.
5. Примеры.
5.1. Пусть 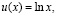 так что
так что
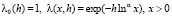 . (5.1)
. (5.1)
При этом (см. (2.3)) 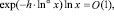 если
если 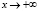 , в чем можно легко убедиться, применяя правило Лопиталя n раз, где n – наименьшее натуральное число, для которого
, в чем можно легко убедиться, применяя правило Лопиталя n раз, где n – наименьшее натуральное число, для которого  Следовательно, при
Следовательно, при 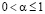 для случая (5.1) выполнены условия п.1 теоремы 2.1, и, следовательно, справедливо ее утверждение. Если же
для случая (5.1) выполнены условия п.1 теоремы 2.1, и, следовательно, справедливо ее утверждение. Если же 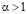 , то
, то 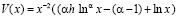 и выражение в скобках возрастает с ростом х, а значит, обращается в ноль ровно при одном значении х. Следовательно, соответствующая последовательность (4.1) кусочно-выпукла. Остается проверить, что (см. (2.5), (1.9)) при всех
и выражение в скобках возрастает с ростом х, а значит, обращается в ноль ровно при одном значении х. Следовательно, соответствующая последовательность (4.1) кусочно-выпукла. Остается проверить, что (см. (2.5), (1.9)) при всех 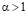
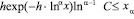
что очевидно для 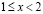 и остается справедливым для
и остается справедливым для 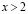 , поскольку функция
, поскольку функция
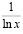

ограничена вместе с функцией вида 
Итак, утверждения теоремы 2.1 справедливы для случая (5.1) при всех 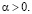 В частности, (случай α=1) сумма ряда
В частности, (случай α=1) сумма ряда
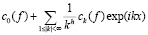
при 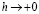 стремится к значениям f(x) для почти всех х (
стремится к значениям f(x) для почти всех х (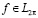 ) и равномерно по х в случае f∈С2π
) и равномерно по х в случае f∈С2π
5.2. Пусть 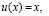 так что
так что
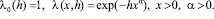 (5.2)
(5.2)
В этом случае получаем обобщенные средние Пуассона (1.4); классические средние Пуассона соответствуют случаю 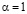 и
и 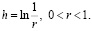
Очевидно, что 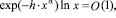 если
если 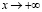 , т.е. выполнено условие (1.7), а тогда при
, т.е. выполнено условие (1.7), а тогда при  для случая (5.2) справедливо утверждение теоремы 2.1. Если же
для случая (5.2) справедливо утверждение теоремы 2.1. Если же 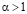 , то функция
, то функция 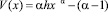 обращается в ноль ровно при одном значении х. Следовательно, соответствующая последовательность (4.1) кусочно-выпукла. Остается проверить, что (см. (2.5), (1.9)) при всех
обращается в ноль ровно при одном значении х. Следовательно, соответствующая последовательность (4.1) кусочно-выпукла. Остается проверить, что (см. (2.5), (1.9)) при всех 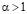
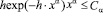 ,
,
что очевидно, поскольку функция  ограничена при всех
ограничена при всех 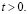
Следовательно, утверждения теоремы 2.1 справедливы для случая (5.2) при всех 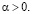 В частности, получаем, что средние (1.4) служат решением обобщенной задачи Дирихле (п. 1), причем граничное условие (1.5) выполняется в виде (1.6) в каждой точке Лебега функции
В частности, получаем, что средние (1.4) служат решением обобщенной задачи Дирихле (п. 1), причем граничное условие (1.5) выполняется в виде (1.6) в каждой точке Лебега функции 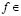
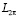 и равномерно по x для всякой f∈С2p.
и равномерно по x для всякой f∈С2p.
Близким к рассмотренному является пример полиномиально-экспоненциального метода суммирования, определяемого (см. (4.1)) функцией
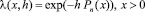 , (5.3)
, (5.3)
где 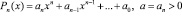 – произвольный многочлен n-й степени,
– произвольный многочлен n-й степени, 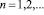 Функция
Функция 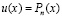 принимает только положительные значения при достаточно больших х; в частности, существует постоянная C>0, такая, что
принимает только положительные значения при достаточно больших х; в частности, существует постоянная C>0, такая, что 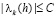 при всех
при всех  В силу (5.3)
В силу (5.3) 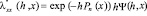 , причем
, причем
 . (5.4)
. (5.4)
Многочлен (5.4) имеет степень 2n – 2, так что меняет знак не более 2n – 2 раз. Следовательно, выполнено условие кусочной выпуклости последовательности (4.1).
Проверим условия (1.9). Имеем в левой части (1.9)
 . (5.5)
. (5.5)
Здесь дробь 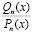 , в которой
, в которой 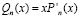 , ограничена, поскольку отношение старших коэффициентов многочленов
, ограничена, поскольку отношение старших коэффициентов многочленов 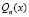
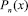 равно n. Первая же дробь в (5.5) ограничена, поскольку она имеет вид
равно n. Первая же дробь в (5.5) ограничена, поскольку она имеет вид 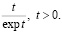 Следовательно, все произведения (5.5) ограничены некоторой постоянной.
Следовательно, все произведения (5.5) ограничены некоторой постоянной.
Итак, условия теоремы 2.1 выполнены для полиномиально-экспоненциальных средних, определяемых функцией (5.3), а значит и в этом случае справедливо ее утверждение.
Заметим, что даже частные случаи основного утверждения (п.2) настоящей работы, исследованные в п.5, являются новыми и представляют самостоятельный интерес.


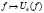 defined by methods of summation
defined by methods of summation 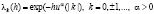 is studied. At some conditions on function
is studied. At some conditions on function 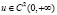 the convergence
the convergence 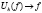 (
( ) in each Lebesque point is established.
) in each Lebesque point is established.