На сегодняшний день актуально использование метапредметных связей при проведении занятий в образовательных учреждениях. Применение метапредметных связей на занятиях способствует формированию основных учебных компетенций:
- вовлечению обучающихся в мировое пространство;
- разностороннему развитию обучающихся, формированию процессуальных умений;
- при подготовке и проведении занятий давать возможность обучающимся реализовать свой творческий потенциал;
- научить учащихся самостоятельно добывать необходимые знания, интерпретировать, творчески перерабатывать их и воспроизводить в осмысленном виде.
На примере задачи: «Моделирование одной антагонистической позиционной игры на взвешенном ориентированном графе» рассмотрим применение метапредметных связей в курсе информатики. Для решения данной задачи необходимы знания следующих дисциплин: алгоритмы на графах, теории игр, основ алгоритмизации и программирования, моделирования и формализации, основ объектно-ориентированного программирования.
Цель работы - проанализировать и смоделировать одну антагонистическую позиционную игру на взвешенном ориентированном графе.
Основной предмет нашего исследования — комбинаторная игра.
Исследование комбинаторной игры показалось нам наиболее интересным, т.к. привлекательным оказывается участие в игре, ее анализ, выработка стратегии, создание играющих (и выигрывающих) программ.
В основе решения задачи лежит теория комбинаторных игр — активно развивающаяся в настоящее время область математики на стыке теории графов, математической логики и теории чисел, которая лежит в основе компьютерных алгоритмов соответствующих игр.
Работа проводилась в несколько этапов.
1. Постановказадачи.
Имеется взвешенный ориентированный прямоугольный граф-решетка размером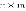 
(где 
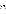– количество вершин графа по горизонтали, 
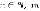– количество вершин графа по вертикали, 
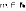) с весами дуг 
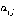и 
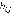(где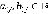 
) - веса соответственно вертикальных и горизонтальных ребер
.
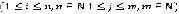Из вершины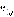 
возможен переход либо в вершину 
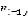, либо в вершину 
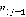(где
).
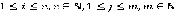Необходимо проанализировать и решить антагонистическую игру на взвешенном ориентированном графе, т.е. рассчитать выигрышные позиции для каждого игрока, а также написать программу, моделирующую игру двух лиц.
2. Определены правила хода для каждого игрока: игроки по очереди рисуют ребра маршрута из s в t, выигрывает тот, у которого сумма его ребер в маршруте больше.
3. Для моделирования игровой ситуации построим игровую математическую модель.
Взвешенный ориентированный прямоугольный граф-решетка размером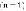 
- это поле игры для двух игроков. В данном графе 
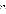вершин и 
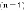ребро по вертикали, 
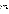вершин и 
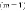ребро по горизонтали.
Пусть, для определенности, в начальной вершине s ход первого игрока. Тогда, принимая за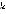 
- количество пройденных ребер, с помощью формулы (
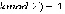(где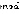 
– операция вычисления остатка от целочисленного деления числа 
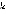на 2) можно легко узнать, ход какого игрока в текущей вершине. Если при подстановке значения 
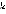получаем 1, то ход первого игрока, если 2– ход второго игрока. В суммарном маршруте игроков 
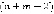ребра. Поэтому в заключительной позиции ход игрока с номером 
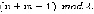В заключительной позиции выиграл первый игрок, если сумма весов его ребер в маршруте больше, чем у второго, и второй, если сумма весов его ребер в маршруте оказалась больше, чем у первого.Пусть 
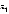- сумма весов ребер в маршруте первого игрока, 
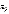- сумма весов ребер в маршруте второго игрока.
Игра антагонистическая, а значит, интересы игроков противоположны.
Первый игрок стремится максимизировать разность сумм весов ребер первого и второго игрока, то есть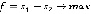 
. Второй игрок, наоборот, стремится минимизировать разность сумм весов ребер первого и второго игрока, то есть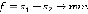 
Напомним, что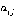 
и 
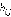(где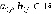 
) - веса соответственно вертикальных и горизонтальных ребер 
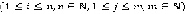Рассмотрим, как рассчитывается функция 
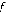для текущего положения игрока.
Пусть в позиции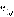 
ход первого игрока. Напомним, что из вершины 
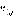возможен переход либо в вершину 
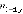либо в вершину
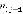(где
.
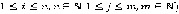Пусть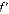 
- максимальное значение функции 
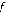. Тогда для первого игрока значение функции 
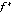в вершине 
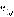равно максимальному значению суммы функций 
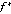для второго игрока в вершинах 
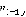и 
и 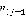соответствующих значений весов ребер 
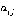или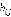 
. Получаем формулу
.
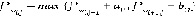Пусть в позиции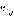 
ход второго игрока. Тогда для второго игрока значение функции 
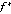в вершине 
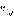равно минимальному значению разности функций 
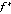для второго игрока в вершинах 
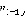и 
и 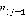соответствующих значений весов ребер 
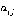или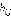 
. Получаем формулу:
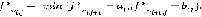
4. Разработка алгоритма решения задачи нахождения значений функции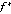
в виде блок-схемы (рис. 1). Алгоритм был разработан на основе идей теории Шпрага-Гранди и методов динамического программирования.
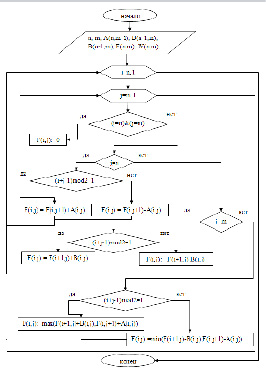
Рисунок 1. Блок-схема алгоритма
Чтобы заполнить матрицу выигрышных позиций, воспользуемся формулой 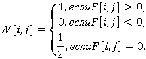(1):
(1)
Получаем, что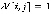 
, если переход в вершину 
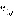выигрышен для первого игрока, и 
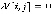, если переход в вершину 
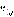выигрышен для второго игрока, 
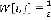в ничейной ситуации.
5. Этот алгоритм был протестирован на нескольких примерах в системе Maple 15.
6. Реализован на языке С++ в среде C++ Builder 6 в консольном приложении и в форме игрового приложения с графическим интерфейсом пользователя.
Согласно проведенным исследованиям, данную задачу можно использовать в процессе изучения дисциплины информатика, используя знания дисциплин математического цикла.