Программа школьного курса не позволяет в полном объеме рассмотреть задачи на решение квадратных уравнений, содержащих параметр (в 9-летней школе). При этом такие задачи включаются в материалы ГИА, ЕГЭ, вступительных испытаниях в различные учебные заведения и вызывают у учащихся трудности. Таким образом, необходимо обучать учеников решению задач на исследование корней квадратного трехчлена, но недостаточно такого типа задач в школьных учебниках. В статье раскрывается возможность решения данной проблемы через введение элективного курса «Квадратный трехчлен в задачах».
School course program does not fully address the challenges the decision quadratic equations with parameter (in the 9-year-old school). These tasks are included in the materials of the GIA, EGE, entrance tests in various educational institutions and students have difficulties. Thus, you need to train students to meet the challenges of the study Trinomial square roots, but not enough of that sort of problem in school textbooks. In the article the opportunity to address this problem through the introduction of the elektive of the course "freaks of cock" tasks.
Квадратный трехчлен с полным правом можно назвать основной функцией, среди изучаемых в школьном курсе математики. Для нее в школьном курсе могут быть достаточно строго доказаны основные свойства, составляющие содержание теории и необходимые для решения задач. В то же время в школьном курсе алгебры рассматриваются лишь самые простые, непосредственные применения свойств квадратного трехчлена в стандартных ситуациях – таких, как решение квадратных уравнений и неравенств, нахождение условий существования решений, определение знаков корней, отыскание наибольшего или наименьшего значения квадратного трехчлена и т.п.
Проанализировав школьные учебники алгебры для 9-го класса, мы убедились в том, что в них задач на исследование квадратного трехчлена незначительно.
В учебнике “Алгебра для 9-го класса с углубленным изучением математики” под редакцией Н.Я. Виленкина приведена одна задача на исследование квадратного трехчлена: найдите все значения а, при которых для всех |х| ≤ 1 выполняется неравенство
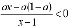 .
.
Это задание относится к неравенствам с параметром, но оно сводится к системе линейных неравенств относительно х.
Также в учебнике “Алгебра для 9-го класса” А.Г. Мордковича приводится одна задача на исследование корней квадратного трехчлена: при каких значениях параметра р квадратное уравнение 3х 2 ‒ 2рх ‒ р + 6 = 0: а) имеет два различных корня; б) имеет один корень; в) не имеет корней [13].
А в учебнике “Алгебра для 9-го класса” под редакцией С.А. Теляковского задач такого типа не приводится.
Программа школьного курса ограничена и не позволяет в полном объеме рассмотреть задачи на решение квадратных уравнений, содержащих параметр. При этом такие задачи часто включаются в материалах ГИА, ЕГЭ, вступительных испытаниях в различные учебные заведения и вызывают у учащихся трудности, обусловленные необходимостью понимания закономерностей, наличия навыка анализа конкретного случая на основе известных общих свойств объекта, систематичности и последовательности в решении, умения объединять рассмотренные частные случаи в единый результат.
Таким образом, необходимо обучать учеников решению задач на исследование корней квадратного трехчлена, но недостаточно такого типа задач в школьных учебниках.
Мы видим возможность решения данной проблемы через введение элективного курса «Квадратный трехчлен в задачах» и разработке методических рекомендаций по его проведению. Так как известно, что элективный курс, улучшает имидж и повышает конкурентоспособность школы, так как реализация данного курса дает более глубокие знания по математике, увеличивает уровень интеллектуального развития учащихся, что благоприятствует их дальнейшему обучению. Курс формирует такие умения и навыки как логичность и самостоятельность мышления, умение обобщать и систематизировать навыки в решении задач.
Разработанный нами элективный курс «Квадратный трехчлен в задачах» предназначен для предпрофильной подготовки школьников в 9-м классе. Он, с одной стороны, поддерживает изучение основного курса алгебры, направлен на систематизацию знаний, реализацию внутрипредметных связей, а с другой – служит для построения индивидуального образовательного пути.
Цель курса: перейти от репродуктивного уровня усвоения материала (простого решения квадратных уравнений и неравенств и задач на их составление) к творческому; научить применять знания свойств квадратного трёхчлена при решении задач.
Данный курс предусматривает использование классно-урочной и лекционно-практической систем, а также личностно-ориентированных педагогических технологий. При решении задач значительное место должны занимать поиски идей решения, эвристические соображения, и только затем, само решение, найденное эвристически, проводится строгим логическим рассуждением.
Теоретическую часть материала предполагается излагать в форме лекции. На всех практических занятиях должна присутствовать самостоятельная работа учащихся: индивидуально, в парах, в группах – в зависимости от уровня обучаемости школьников. Такая организация способствует реализации развивающих целей курса, так как развитие способностей учащихся возможно лишь при сознательном, активном участии в работе самих учащихся.
Содержание курса может быть освоено как в коллективных, так и в индивидуально-групповых формах.
Содержание изучаемого курса:
Квадратное уравнение и его корни. Определение квадратного уравнения. Дискриминант квадратного уравнения. Корни квадратного уравнения. Степень трехчлена. Число корней квадратного уравнения.
Теория Виета. Знаки корней квадратного уравнения. Соотношения на корни квадратного трехчлена. Теорема Виета для полного и приведённого квадратного уравнения. Условия, определяющие знаки корней квадратного уравнения. Решение задач на применение теоремы Виета и обратной ей, определение знаков корней квадратного уравнения, на соотношение между корнями квадратного трехчлена.
Расположение корней квадратного уравнения. Графическая характеристика расположения корней квадратного уравнения на числовой прямой по отношению к фиксированному числу.
4. Решение квадратных уравнений и неравенств с параметром. Решение квадратных уравнений и неравенств для всех значений параметра.
Критериями эффективности используемой методики обучения математики учащихся являются: качество овладения учащимися предметным содержанием элективного курса, повышение интереса к творческой деятельности. Качество овладения учащимися предметным содержанием элективного курса определяется по результату контрольных работ.
Апробация материалов элективного курса проводилась в 2013 году в 9-ом классе и в начале учебного года 10-го класса МБОУ СОШ с. Кипчак-Аскарово Альшеевского района и состояла из следующих этапов:
I констатирующий этап. Анализ психолого-педагогической, методической, математической литературы по проблеме исследования. Выбор контрольных работ и экспериментального класса.
Контрольная работа для 9-го класса по теме “Квадратный трехчлен”, содержит также задания с параметром. Цель: проверить усвоение программного материала и умение решать задачи в новой ситуации.
Вариант I.
1. Найдите корни квадратного трехчлена:
а) х2 ‒ 3х ‒ 10; б) ‒ 2х2 + х +15.
2. При каких значениях b квадратный трехчлен х2 ‒ 2х + b можно разложить на линейные множители?
3. При каких значениях b в разложении данных квадратных трехчленов 4х2 ‒ 3х ‒ 1; х2 + 2х ‒ b может быть один и тот же линейный множитель?
Вариант II.
1. Найдите корни квадратного трехчлена:
а) х2 ‒ 5х ‒ 24; б) ‒ 3х2 ‒ х +14.
2. При каких b квадратный трехчлен х2 ‒ 4х + b можно разложить на линейные множители?
3. При каких значениях b в разложении данных квадратных трехчленов 2х2 ‒ х ‒ 1; х2 + 4х ‒ b может быть один и тот же линейный множитель?
II этап. Обучающий эксперимент. Цель второго этапа ‒ обеспечить повторение, обобщение и систематизацию материала темы; повысить интерес учащихся к изучению математики и её приложениям. Проведено 12 занятий по теме “Квадратный трехчлен в задачах”.
III этап. Констатирующий эксперимент. Проведение итоговой контрольной работы по усвоению материалов элективного курса “Квадратный трехчлен в задачах”, сравнение с результатами первой контрольной работы.
Анализ результатов усвоения у учащихся 9-ого класса: “5” – 25%, “4” – 42%, “3” – 33%.
Анализ результатов усвоения у учащихся 10-ого класса: “5” - 25%, “4” – 47%, “3” – 28%.
Таким образом, исходя из III этапа, сравнивая контрольные работы, мы сделали вывод об успешном усвоении учащимися материалов элективного курса.
Данный элективный курс может иметь свое продолжение в 10-м классе по теме «Уравнения и неравенства с параметром, сводящиеся к квадратным».
Элективные курсы – это новейший механизм актуализации и индивидуализации процесса обучения. С хорошо разработанной системой элективных курсов каждый ученик может получить образование с определенным желаемым уклоном в ту или иную область знаний.
Таким образом, элективные курсы незаменимы для достижения основных целей образования на старшей ступени школы.

