Вот уже в течение нескольких лет в Кубанском государственном технологическом университете, а так же в его Армавирском филиале, создается информационная образовательная среда вуза, кафедр. Так, на кафедре общенаучных дисциплин АМТИ накоплено достаточно большое количество обучающих интерактивных документов [1], [2], [3], [4].
Авторами данной статьи в среде математического пакета MathCAD 14 разработаны обучающие интерактивные документы по изучению поверхностей второго порядка. Один из авторов (Мягкова Э.С.) предложил построить 3-мерные графики некоторых поверхностей, в частности эллиптический параболоид (уравнение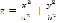 
), гиперболический параболоид (уравнение 
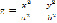) средствами мат.пакета. Это оказалось очень просто и увлекательно. Особенно эффектно стал выглядеть график в движении после заливки поверхности цветной палитрой, нанесении каркасных линий и т.д. (работа со свойствами графика) (рисунок 1).
Построить самостоятельно графики таких поверхностей как одно- и двуполостный гиперболоид, эллипсоид и цилиндр предстояло другому автору (Козленко Р. C.) Первое затруднение вызвала необходимость выразить из исходного уравнения одно- и двуполостного гиперболоида, эллипсоида переменную z, отсечь мнимые части комплексных корней. Поверхность строилась состоящей из двух частей, неизбежным оказывалось появление плоскости, соединяющей их (рисунок 2).
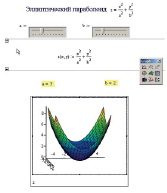
Рисунок 1. Эллиптический параболоид
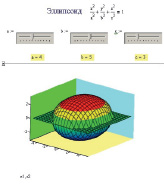
Рисунок 2. Эллипсоид
А вот построение цилиндрических поверхностей: эллиптического цилиндра (уравнение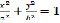 
), параболического цилиндра (уравнение 
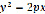) оказалось затруднительным из-за невозможности выразить из уравнения переменную z. Автору (Козленко Р.) пришлось самостоятельно изучить вопрос о параметрическом задании кривых и поверхностей. (Первоначальные сведения о параметрических уравнениях линии, в частности прямой, были освещены на лекциях по математике, в разделе Аналитическая геометрия.) И только перейдя к параметрическим уравнениям поверхности, используя специальную встроенную функцию MathCAD CreateMesh, удалось получить желаемые 3d-графики (рис. 3, 4).
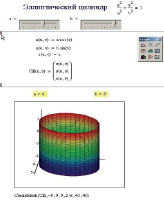
Рисунок 3. Эллиптический цилиндр
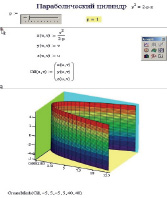
Рисунок 4. Параболический цилиндр
Оказалось, что при переходе к параметрическим уравнениям сферы, эллипсоида, можно получить изображения поверхностей без соединяющей плоскости!
Изюминкой разработанных обучающих интерактивных документов стало использование такого элемента как Slider (ползунок). Перемещение указателя ползунка приводит к изменению параметров, входящих в уравнение, и плавной деформации поверхности.
Таким образом, применение современных информационных технологий позволяет не только эффективно визуализировать изучаемый студентами материал. Внешняя простота и привлекательность работы с использованием СИТ способствует активизации умственной и творческой деятельности студента, развитии соответствующих профессиональных компетенций. Так, естественный интерес привел созданию целой серии обучающих интерактивных документов, вошедших в информационную образовательную среду кафедры и учебного заведения в целом.