Среди многих задач, которые решает управление качеством (УК), в том числе в сфере образовательных услуг, наиболее важными являются задачи результативности (достигнут ли запланированный результат), эффективности (какой ценой достигнут результат и насколько эффективно работает система), оптимизации (способы оптимизации системы или процесса). Эти задачи неразрывно связаны с понятиями «валидация» и «верификация». Валидация – проверка на валидность. Верификация - это подтверждение соответствия определённым эталонным требованиям. Одним из методов, широко применяемых в УК, является метод ранжирования – приведения значений параметра объектов системы в соответствие рангу (номеру объекта ранжирования) в порядке убывания этого параметра и представление результатов в виде рейтинга. Однако, этот метод недостаточно объективен, так как верхние и нижние границы эффективности систем по рейтинговым таблицам устанавливаются, как правило, субъективным решением судей: проводится черта, ниже которой система объявляется неэффективной и требующей оптимизационных процедур.
В методологии науки известен метод рангового анализа (РА) (ценологический подход), который используется при решении подобных задач [1-5]. При этом этот метод опирается на строгий математический аппарат и доказательность (в отличие от описанного выше). Теория РА для техноценозов была разработана и внедрена в практику профессором МЭИ Б.И. Кудриным (wwwkudrinbi.ru) более 30 лет назад [1] и перенесена его последователями на другие области знаний, в том числе на область образования [3-5] (www.gurinarv.ulsu.ru ).
Однако, РА до сих пор не рассматривался в сфере УК как метод улучшения эффективности систем. Первые предложения по применению РА в УК образования изложены в [6]. Рассмотрим основные направления применения РА в УК на примере образовательных систем, проверенные на практике.
1. Сущность метода рангового анализа
Многие реальные системы объективного мира, как естественнонаучные так и социальные, являются ценозами. Ценоз – это сообщество. Особь – элемент (единица) ценоза, он же и объект ранжирования. В технике «особи» – технические изделия. Такая терминология перенесена из теории биоценозов. Однако не любое сообщество – ценоз. Система является ценозом, если ранговое распределение (РР) объектов в нём представляет собой гиперболическую функцию [1]:
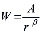 , (1)
, (1)
где W – ранжируемый параметр системы, r – ранговый номер элемента (особи) в ней (1, 2, 3…), А – максимальное значение параметра W с рангом r =1, b – ранговый коэффициент, или степень крутизны гиперболы. Впервые же гиперболические РР описал Ципф применительно к текстам (W – частота, с которой встречается определённое слово в тексте) [7].
Ядром РА (ценологического подхода) является применение гиперболического закона РР (1). Идеальный ценоз-система устойчив, любые отклонения его элементов от гиперболической зависимости в РР (1) вносит в неё дисбаланс и неустойчивость и требуют оптимизации. Оптимизация заключается в устранении аномальных отклонений от закона РР (1).
На большом статистическом материале было доказано, что гиперболический закон РР (1) справедлив для образовательных систем, являющихся ценозами, объекты ранжирования в которых – учащиеся, классы, школы и т.д., а их параметры – это успеваемость, рейтинг в баллах, показатели эффективности и т.п. [3-5]. Следовательно, РА можно и целесообразно применять в УК образования. Применение РА в УК включает 2 этапа [6].
I. Проверка системы на «ценозность»: построение табулированного, а затем графического РР; аппроксимация РР зависимостью (1) с помощью компьютерных программ и определение параметров РР: b , А, квадрата коэффициента регрессии R^2, который показывает степень приближения реального РР к теоретическому (1).
II. Анализ результатов и выявление возможностей применения РА к процедурам валидации, верификации, оптимизации.
2. Применение метода рангового анализа в системе образования
А) Оценка валидности тестовых заданий [3-7].
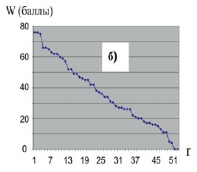
В системе образования РА применяется для проверки надёжности и валидности (пригодности) олимпиадных, контрольных и тестовых заданий. Правильно составленные и правильно проверенные олимпиадные, тестовые и контрольные задания приводят к результатам, которые отражаются гиперболическим законом РР учащихся в рейтинге. Построение графических РР необходимо, так как РР в виде списка не даёт информации о характере убывания: оно может происходить по другому закону. На рис. 1 приведены примеры реальных РР абитуриентов по результатам ЕГЭ (рис.1, а) и студентов по результатам контрольного тестирования (рис. 1, б) [6]. Элитные объекты в любом ценозе согласно (1) составляют меньшинство. Из графика (а) рис.1 видно: высокие баллы по математике – более 70 – получили лишь 5 человек из 117 выпускников школ, поступивших в 2011 году на инженерно-физический факультет высоких технологий (ИФФВТ) УлГУ (4,3%) при максимальном балле 82.
 а
а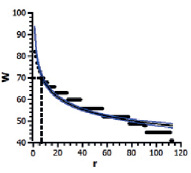 б
б
Рис. 1. Графики РР (W– балл, r – ранговый номер учащегося): а) рейтинг ЕГЭ по математике абитуриентов ИФФВТ УлГУ 2011 г., β = 0.14; R^2 = 0.90; б) рейтинг студентов 1 курса ИФФВТ УлГУ по результатам теста по физике (1 сем., 2011 г.).
По обе стороны аппроксимационной кривой – контуры линий доверительного интервала, составляющего 0,95. R^2 = 0,9 показывает высокую степень приближения эмпирических точек к теоретической гиперболе. Аналогичные графики (не приводятся) получены для РР результатов по физике и обществознанию. По физике лишь 3,3% из 90 чел. получили более 70 баллов; по обществознанию – 12% из 25 абитуриентов.
Из графика рис 1, б следует, что по результатам теста рейтинг студентов распределён равномерно: сильных, средних и слабых поровну (по 1/3 в каждой категории), что не может соответствовать реалиям. Это подтвердили результаты экзамена в конце 1 семестра по этому предмету, показавшие гиперболическое РР учащихся. Следовательно, тест был недостаточно валидный и надёжный. Любые недочёты в рейтинговой системе оценки, валидности и надёжности тестовых заданий дают искажения в форме РР. Это утверждение верно лишь при наличии адекватных организационных условиях проведения оценочных мероприятий.
Целесообразно выделение нескольких (3-5) уровней валидности. Например, грубая шкала 3-х уровней валидности выделяет:
- высокий уровень валидности на графике выражается гиперболой с высоким уровнем аппроксимации формулой (1) с R^2 около 0,9 (рис.1,а).
- средний уровень (удовлетворительная валидность) – РР представляет линейную зависимость (рис.1,б), либо гипербола сильно искажена;
- 0-валидность, при этом графики РР – это прямые, параллельные оси рангов (все учащиеся имеют одинаковый балл);
Б) Определение качества рейтинговой системы оценки образовательных учреждений.
Ценологический подход позволяет оценить адекватность системы критериев, по которой выстраивается рейтинг и определяются лучшие образовательные учреждения (ОУ) региона, страны. На рис. 2, а представлен эмпирический график рейтинга 100 лучших (наиболее эффективных) вузов России в 2012 году, представляющий собой гиперболу. Параметры взяты из известной рейтинговой таблицы «Рейтинг ВУЗов России, 2012 г.» (оценку провело рейтинговое агентство "Эксперт»). Из графика видно, что система рейтинговой оценки вузов, в целом, адекватна: R^2 = 0.8. Однако эмпирическая кривая имеет горб и отклонение вниз в хвостовой части. Уровень валидности – между средним и высоким. Следовательно, данная рейтинговая система не совершенна и требует доработки.
Для сравнения на рис. 2, б приведён график РР 100 лучших средних ОУ России [3, с. 16]. Он был построен по табулированным данным журнала «Карьера» (2001, №4. – С.72-84). Как видно из графика, эмпирические точки хорошо ложатся на теоретическую кривую аппроксимации. О высоком уровне адекватности данной системы критериев свидетельствует очень высокий показатель регрессии, близкий к единице: R^2 =0,96.
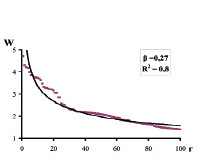
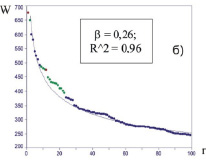
Рис. 2 . РР рейтинга ОУ России; W – рейтинг в баллах, r – ранговый номер ОУ. а) РР 100 лучших вузов России 2012 г. по итоговому рейтинговому функционалу W; r =1 – МГУ; r =2 – МГТУ им. Н.Э.Баумана; r =90 – Ульяновский госуниверситет; r =100 – Новосибирский госуниверситет экономики и управления. б) РР 100 лучших средних ОУ России в 2000 г. ; r =1 – Московская экономическая школа; r =100 – гимназия № 1518 (г. Москва) [3, с. 16].
Таким образом, система критериев и показателей предложенная и реализованная жур-налом «Карьера» в 2000 г., имеет более высокий уровень валидности, чем система оценки вузов 2012 года.
В) Оптимизация педагогических систем с позиций РА
Конечной целью РА является оптимизация системы-ценоза. Рассмотрим суть приме-нения РА для оптимизации педагогических систем. Как правило, реальное РР отличается от идеального следующими видами отклонений [2, 3]:
- Некоторые эмпирические точки выпадают из идеального распределения, образуя «горбы» и «впадины».
- Эмпирическая гипербола по сравнению с теоретической, имеет заваливающийся вниз «хвост» с областью маргинальных объектов (в техноценозах это до предела изношенная техника, в учебных группах – кандидаты на отчисление).
- Эмпирический график сильно искажён, либо гипербола вырождена в другие графические зависимости.
На рис. 1 в графиках мы видим типичные отклонения второго (рис. 1, а) и третьего (рис. 1, б) видов.
Оптимизация любого ценоза предполагает определение способов и средств его улучшения. После выявления аномалий на графике РР, по табулированному распределению определяются элементы (особи), «ответственные» за аномалии, и намечаются мероприятия по их устранению [2]:.
- Номенклатурная оптимизация – целенаправленное изменение численности ценоза, устремляющее РР ценоза по форме к идеальному: отсев неуспевающих в учебной группе, избавление от «плохих» вузов» и т.п..
- Параметрическая оптимизация педагогического ценоза – это улучшение параметров успеваемости объектов «хвостовой области» РР.
Закон (1) даёт объяснение того факта, что лучших особей в любом ценозе мало – в среднем не более 20%, что соответствует закону Парето 80/20 [10]. Лучшие объекты ценоза (20%) представляет элиту. Основной же «вес» в гиперболическом РР, как и в законе Парето, принадлежит среднестатистическому большинству («саранчёвой касте») [1, 2].
Понимание и использование специалистами и учащимися принципа 80/20 и закона (1) даёт реальное представление об окружающем мире и свидетельствует о наличии ценологиче-ского мышления, которое характеризуется осознанием учащимися своего места в ранговой системе, позволяет оценить свои возможности в постановке реальных целей и задач, моти-вирует и побуждает к действию – найти средства, с помощью которых каждый учащийся сможет улучшать достижения.
Выводы
- Сфера УК пополнена ценологическим подходом, а её категорийный аппарат совокуп-ностью понятий рангового анализа.
- Применение РА в УК образования может быть осуществлено в направлениях:
– в оптимизации учебного процесса, сущность которого заключается в устране-нии аномальных отклонений в РР («хвостов», «горбов», «впадин»);
– в технологиях оценки и контроля качества образования в образовательных уч-реждениях и для оценки валидности тестов и контрольных заданий;
- в прогнозировании результатов обучения (например, количеству медалистов в классе, количество двоек или отличных оценок на группу на любом экзамене, должно составлять не более 20 % от общего числа оценок).

