Введение
Современное понимание результата образовательного процесса находит свое отражение в конкретном учебном продукте, через который обучающиеся проявляют личные достижения по усвоению профессиональных знаний, умений и способности решать комплексные профессионально-ориентированные задачи.
Понятия «учебные достижения», «учебно-профессиональные достижения» приобрели в настоящее время актуальное значение. Они представляют собой многомерные и целостные профессионально-личностные качества будущего рабочего или специалиста, наряду с общими и профессиональными компетенциями являются требованиями к результатам обучения в ФГОС – третьего поколения.
Цель исследования – научное обоснование процедуры выявления, измерения и оценивания учебно-профессиональных достижений в процессе профессионального обучения.
Для достижения цели исследования были выбраны методы исследования: теоретические методы (изучение и анализ философской, психологической, педагогической и методической литературы, нормативной документации); эмпирические – психолого–педагогические методы сбора информации (тестирование, сбор, обработка и представление результатов опытно-экспериментальной работы с помощью программы RUMM 2030).
Учебные достижения, подчеркивает И. В. Гладкая [2], предполагают субъективное переживание результата. В подтверждение данной позиции представляем вывод, сделанный в исследовании Л. С. Илюшина [2], который предлагает рассматривать достижения, как категорию, отражающую степень прогресса личности по отношению к её предшествующим проявлениям в образовательной деятельности. Однако на наш взгляд, эвристический смысл понятия «учебно-профессиональные достижения» правомерно соотнести с «родственными» ему понятиями «личный потенциал», «профессиональные достижения», «профессионально-личностный потенциал работника», «человеческий фактор», «личный фактор», активно используемыми сегодня не только в профессиональной педагогике, но и в социально-экономических науках.
Совпадая по смыслу с социально-экономическими категориями, характеризующими процесс живого труда, понятие учебно-профессиональные достижения нетождественно им. Прежде всего, это интегральное понятие. В данном случае оно не сводимо к «личностному фактору» или к «человеческому фактору» производства. «Человека производства» каждое из экономических понятий трактует ограниченно. В них производственная или профессиональная способность личности рассматривается преимущественно с точки зрения производственного цикла, а сам работник невольно низводится до роли простого носителя производственных функций.
В противовес узко экономической трактовке педагогическое понимание понятия «учебно-профессиональные достижения» не только в теоретическом, но и в операциональном плане максимально ориентирована на представление о личности обучаемого как целостном субъекте образовательного процесса. Целостность в данном случае означает:
1. Способность к самообразованию и саморазвитию. Как интегральное понятие, «учебно-профессиональные достижения» характеризуют внутреннюю духовную энергию обучаемого, его деятельную позицию, направленную на творческое самовыражение и общественное самоутверждение, самореализацию.
2. Полноту выраженности личностных свойств и качеств обучаемого, обеспечивающих в своей системной совокупности его способность выступать в роли активного субъекта учебно-профессиональной деятельности. Многомерная структура учебно-профессиональных достижений, включает следующие основания: а) профессиональные знания, умения и навыки, обусловливающие профессиональные компетенции (квалификационный потенциал обучаемого); б) работоспособность (психофизиологический потенциал); в) интеллектуальные, познавательные способности (образовательный потенциал); г) креативные способности (творческий потенциал); д) способность к сотрудничеству, коллективной организации и взаимодействию (коммуникативный потенциал); е) ценностно-мотивационную сферу (идейно-мировоззренческий, нравственный потенциал).
3. Структурное единство внутренних элементов. Уровень развития учебно - профессиональных достижений, как и степень соответствия его будущей профессиональной квалификации и эффективности его трудовых функций, зависит не столько от какого-либо одного элемента, сколько от способа их интеграции, внутренней сбалансированности всех компонентов, придающей, новую, «дополнительную силу» профессиональным способностям [6].
Рассмотрение понятия «достижение» и соотнесение его с другими терминами позволило нам сформулировать определение учебно-профессиональных достижений – это нормативный личностно - образовательный результат, представляющий собой устойчивую совокупность свойств личности обучаемого, репрезентирующих его возможности на различных этапах профессионального обучения и ориентированные на развитие профессиональной деятельности в будущем.
Учебно-профессиональные достижения не сводятся к общим и профессиональным компетенциям, сформированными на определённом этапе профессионального обучения. Принципиальными отличиями является динамика развития личностных качеств будущего рабочего или специалиста, которая проявляется в его возможностях достигнуть профессиональную компетентность на этапе освоения профессии в будущем. Благодаря этим возможностям деятельность рабочего или специалиста становится эффективнее других в профессиональной деятельности. Обобщая выше описанное, можно сделать выводы, что ориентация профессионального образования на формирование у обучаемых учебно-профессиональных достижений выводит его вектор развития на саморазвитие в будущем.
Самостоятельной проблемой современного образования является система выявления, измерения и оценивания сложных, интегративных образовательных результатов. Возникает задача выявления и измерения трудно определяемого свойства. В этом случае исследователи обращаются к процедуре операционализации. Социологический энциклопедический словарь операционализацию представляет как специфическую научную процедуру установления связи концептуального аппарата исследования с его методическим инструментарием посредством образования системы эмпирических показателей характеризующих изучаемый объект [4, с. 219]. Таким образом, создается детальный образ измеряемой латентной переменной. В.С. Аванесов предлагает в данном случае использовать теоретические основы измерения латентных переменных, в основу данной теории положена идея соответствия наблюдаемых результатов измерения модели Г.Раша [1, с.14]. Набор эмпирических показателей (индикаторных переменных) выступает измерительным инструментом. «Индикатор (от лат. indicator - указатель) – основной источник информации о состоянии управляемого объекта и самой системы управления» [3, с.199]. Индикаторные переменные оценивается в «логитах» - принятой единице измерения латентных переменных.
Следовательно, для измерения учебно-профессиональных достижений необходимо создать модель измерения через набор эмпирических показателей (индикаторных переменных). Состав учебно-профессиональных достижений включает уровень сформированности профессиональных знаний, обобщенных практических умений и владение конкретными технологиями конкретного производства. Например, по профессиональному модулю «Изготовление вставок в ювелирные изделия» вариант диагностической работы ориентирован на выявление уровня сформированности учебно-профессиональных достижений через модель, включающую выявление знаниевых компоненты профессиональных компетенций: ПК 2.1. «Анализировать характеристики материала вставок»; ПК 2.2. «Выполнять операции огранки ювелирных вставок»; ПК 2.3. «Контролировать качество огранки» [5]. Обобщенная модель знаниевой структуры учебно-профессиональных достижений по рассматриваемому профессиональному модулю включает следующую структуру: назначение вставок, их классификация, типовые элементы конструкции, материалы из которых изготавливаются вставки, оборудование, охрана труда ювелира, технология изготовления вставок в ювелирные изделия. В качестве метода диагностики знаний обучаемых был выбран метод тестирования. Сформированный тест состоял из 60 заданий в тестовой форме закрытого типа с одним правильным вариантом ответа, нацеленного на выявление качеств освоения обучающимися учебных элементов, входящих в состав профессиональных компетенций. Тестовые задания были разделены на четыре группы. В первую группу вошли 19 заданий, определяющие характеристики ювелирных камней, их классификацию, свойства, применение. В рассматриваемой группе заданий в тестовой форме выявляются знания о свойствах камней (оптические, физические и т.д.), их классификацию по шкале Мооса или по Киевленко Е.В. Вторая группа заданий в тестовой форме включала 9 заданий. В этой группе заданий в тестовой форме определялись знания о видах, формах и типах огранок камней. Третья группа заданий в тестовой форме по технологии изготовления вставок для ювелирных изделий включала 15 заданий в тестовой форме. Четвертая группа заданий по организации и охране труда на рабочем месте при изготовлении вставок в ювелирные изделия состояла из 17 заданий.
Система заданий в тестовой форме подверглась анализу с целью определения возможности ее использования для заключительной диагностики знания обучающихся. Полученные результаты тестирования послужили основанием для коррекции комплекса тестовых заданий с определением такого их состава, который было бы возможным использовать в качестве инвариантного учебного материала.
В тестировании приняли участие обучающиеся одной группы профессии 072500.02 «Ювелир», общей численностью 18 человек. Каждому были предложены тестовые задания, выполнение которых фиксировалось с помощью дихотомической шкалы: 0 баллов – «задание не выполнено или выполнено неверно» и 1 балл – «задание выполнено верно». Установлено, что результат решения заданий в тестовой форме прямо пропорционален оцениваемой латентной переменной «знание теоретических основ технологии изготовления вставок в ювелирные изделия». Полученные результаты были обработаны с помощью программы RUMM 2030, при этом была задействована ее возможность давать характеристику отдельным тестовым заданиям.
Проведенный анализ показал, что сформированные задания в тестовой форме могут быть использованы в целях диагностики знаний по технологии изготовления вставок. Подтверждением тому служит значение степень соответствия индикаторов модели измерения, которое определяется по значению статистики χ2 (ChiSq[Pr]), в таблице 1, Эмпирический уровень значимости статистики χ2, составивший 0,082, что превышает номинальное значение равное 0,05. Это означает, что разработанные задания в тестовой форме можно использовать как для измерения уровня сформированности знаний обучающихся, так и для измерения уровня трудности заданий.
Таблица 1
Статистические характеристики тестовых заданий
|
Номер тестового задания |
Уровень трудности (логиты) |
Стандартная ошибка (в логитах) |
Значение статистики Хи-квадрат |
Уровень значимости статистики Хи-квадрат |
|
I0018 |
-1,887 |
1,014 |
0,744 |
0,689 |
|
I0025 |
-1,782 |
0,971 |
2,085 |
0,353 |
|
I0057 |
-1,782 |
0,971 |
2,085 |
0,353 |
|
I0055 |
-1,130 |
0,758 |
1,771 |
0,412 |
|
I0005 |
-1,053 |
0,739 |
4,536 |
0,104 |
|
I0037 |
-1,053 |
0,739 |
4,536 |
0,104 |
|
I0022 |
-0,993 |
0,724 |
0,483 |
0,786 |
|
I0054 |
-0,993 |
0,724 |
0,483 |
0,786 |
|
I0011 |
-0,805 |
0,682 |
3,489 |
0,175 |
|
I0020 |
-0,783 |
0,678 |
3,432 |
0,180 |
|
I0052 |
-0,783 |
0,678 |
3,432 |
0,180 |
|
I0029 |
-0,627 |
0,647 |
1,965 |
0,374 |
|
I0023 |
-0,555 |
0,635 |
0,512 |
0,774 |
|
I0046 |
-0,541 |
0,632 |
1,383 |
0,501 |
|
I0012 |
-0,506 |
0,627 |
1,884 |
0,390 |
|
I0043 |
-0,341 |
0,601 |
2,869 |
0,238 |
|
I0017 |
-0,329 |
0,600 |
1,339 |
0,512 |
|
I0049 |
-0,329 |
0,600 |
1,339 |
0,512 |
|
I0001 |
-0,303 |
0,596 |
5,044 |
0,080 |
|
I0033 |
-0,303 |
0,596 |
5,044 |
0,080 |
|
I0032 |
-0,285 |
0,593 |
0,582 |
0,748 |
|
I0050 |
-0,195 |
0,582 |
1,264 |
0,532 |
|
I0044 |
-0,160 |
0,577 |
3,982 |
0,137 |
|
I0014 |
-0,158 |
0,577 |
5,200 |
0,074 |
|
I0003 |
0,011 |
0,558 |
0,700 |
0,705 |
|
I0008 |
0,039 |
0,556 |
2,425 |
0,297 |
|
I0015 |
0,039 |
0,556 |
2,425 |
0,297 |
|
I0040 |
0,039 |
0,556 |
2,425 |
0,297 |
|
I0047 |
0,039 |
0,556 |
2,425 |
0,297 |
|
I0034 |
0,043 |
0,555 |
0,436 |
0,804 |
|
I0060 |
0,054 |
0,554 |
3,385 |
0,184 |
|
I0045 |
0,058 |
0,554 |
1,025 |
0,599 |
|
I0013 |
0,085 |
0,551 |
1,013 |
0,603 |
|
I0007 |
0,118 |
0,548 |
2,642 |
0,267 |
|
I0027 |
0,118 |
0,548 |
2,642 |
0,267 |
|
I0039 |
0,118 |
0,548 |
2,642 |
0,267 |
|
I0059 |
0,118 |
0,548 |
2,642 |
0,267 |
|
I0041 |
0,125 |
0,548 |
0,447 |
0,800 |
|
I0035 |
0,303 |
0,534 |
0,023 |
0,989 |
|
I0002 |
0,312 |
0,533 |
1,305 |
0,521 |
|
I0031 |
0,312 |
0,533 |
1,305 |
0,521 |
|
I0021 |
0,324 |
0,532 |
1,597 |
0,450 |
|
I0053 |
0,324 |
0,532 |
1,597 |
0,450 |
|
I0016 |
0,339 |
0,531 |
4,472 |
0,107 |
|
I0048 |
0,339 |
0,531 |
4,472 |
0,107 |
|
I0009 |
0,389 |
0,528 |
1,299 |
0,522 |
|
I0006 |
0,554 |
0,520 |
2,469 |
0,291 |
|
I0038 |
0,554 |
0,520 |
2,469 |
0,291 |
|
I0051 |
0,613 |
0,517 |
1,156 |
0,561 |
|
I0024 |
0,761 |
0,513 |
10,297 |
0,006 |
|
I0056 |
0,763 |
0,513 |
10,286 |
0,006 |
|
I0028 |
0,797 |
0,512 |
3,770 |
0,152 |
|
I0030 |
1,108 |
0,510 |
2,789 |
0,248 |
|
I0019 |
1,162 |
0,511 |
0,174 |
0,917 |
|
I0010 |
1,163 |
0,511 |
0,751 |
0,687 |
|
I0004 |
1,178 |
0,511 |
1,850 |
0,396 |
|
I0042 |
1,179 |
0,511 |
0,753 |
0,686 |
|
I0058 |
1,205 |
0,511 |
0,762 |
0,683 |
|
I0036 |
1,458 |
0,518 |
0,618 |
0,734 |
|
I0026 |
1,532 |
0,521 |
1,185 |
0,553 |
В данной таблице тестовые задания расположены в порядке возрастания их трудности. Поэтому представляется целесообразным рассмотреть их более подробно.
Характеристики тестовых заданий позволили выделить основные типы: 1) «идеальные» задания, которые в наибольшей степени подходят для диагностики профессионально значимых знаний, так как значение статистики χ2 по ним превышает 0,9 (i35, i19); 2) неадекватные задания, обладающие наименьшим значением данной характеристики, не превышающим минимально установленный ее уровень (i24, i56, i16, i48); 3) задания, имеющие высокий уровень трудности (i26, i36, i58, i42, i04, i10, i19, i30); 4) задания, имеющие низкий уровень трудности (i18, i25, i57, i55, i05, i37). С учетом полученных данных был проведен анализ несовместимых с общим набором тестовых заданий (i24, i56, i16, i48), которые были удалены из набора тестовых заданий.
На рис. 1 по оси абсцисс откладываются значения измеряемой латентной переменной уровень знаний обучающихся, по оси ординат – число испытуемых (вверху) и заданий (внизу). Причем, с левой стороны указаны абсолютные значения индивидов/заданий, а с правой – соответствующие относительные величины (проценты).
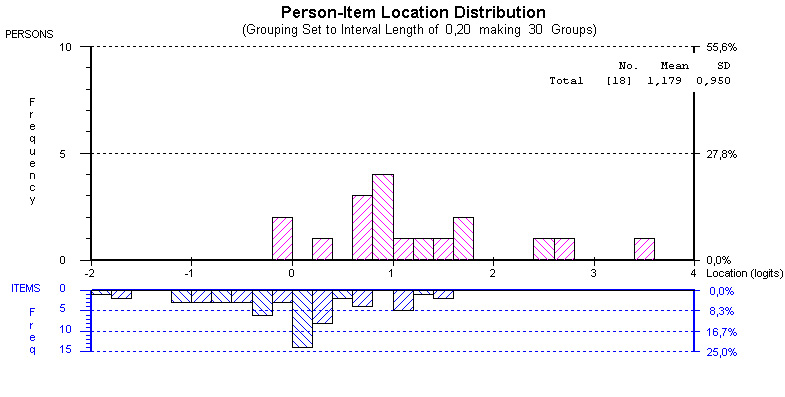
Рис. 1. Соответствие между уровнем знаний обучающихся и трудностью тестовых заданий
В идеальном случае гистограмма распределения трудностей заданий теста (нижняя часть рисунка) должна быть близка к равномерному закону распределения данных. Это означает, что представленный набор заданий позволяет с одинаковой точностью оценивать уровень подготовленности студентов на всем диапазоне измерения. Однако из рис. 1 следует, что это требование не выполняется в не в полной мере.
Исследованиями установлено, что средняя трудность заданий не должна отличаться от среднего уровня подготовленности испытуемых более чем на 0,5 логит. В данном случае средний уровень знаний обучающихся на 1,18 логит превышает средний уровень трудности теста. Этот результат можно интерпретировать двояко: обучающиеся очень хорошо подготовлены, или набор заданий слишком легкий. Следовательно, можно сделать вывод, что представленный вариант заданий в тестовой форме не оптимален в отношении точности измерения. Обучающиеся с высоким уровнем знания оцениваются с меньшей точностью, чем обучающиеся со средним или низким уровнями знаний. Поэтому желательно дополнить задания с более высоким уровнем трудности.
Диапазон варьирования трудности заданий: для анализируемого набора заданий меры трудности распределены от -2,0 до +1,5 логит. Таким образом, диапазон варьирования (размах) значений этой меры заданий равен 3,5 логит. Такой диапазон варьирования трудности тестовых заданий обеспечивает измерение как низкого, так и высокого уровня знания обучающихся. По этому аспекту имеющийся набор тестовых заданий не нуждается в корректировке.
В теории измерения латентных переменных доказано, что равномерность распределения заданий по трудности: трудность соседних заданий не должна отличаться более чем на 0,5 логита, в противном случае принимается, что уровень подготовленности студентов внутри таких «пропусков» не дифференцируются с требуемой точностью. В данном случае таких пропусков нет, и по этому критерию данный тест является хорошим измерительным инструментом.
Соответствие тестового задания модели измерения определяется следующим образом. Обучающиеся по полученным оценкам своих уровней знаний (на основе модели Раша) делятся на три группы: с низким, средним и высоким уровнем знаний. Далее для каждой группы вычисляется среднее значение и на основе критерия Хи-квадрат определяется степень близости этих трех экспериментальных точек характеристической кривой. В результате по эмпирическому уровню значимости статистики Хи-кварат выделяются две группы тестовых заданий: те, которые соответствуют модели Раша, и те, которые не соответствуют модели измерения (неадекватные модели тестовые задания). Для первой группы заданий эмпирический уровень значимости больше 0,05, для второй – меньше. В качестве примера рассмотрим наиболее адекватное тестовое задание и наименее адекватное тестовое задание соответственно.
Характеристическая кривая задания в тестовой форме № 35 «Используемое приспособление или инструмент для измерения размеров изделия…» приведена на рис. 1. Тестовое задание № 35 лучше всего дифференцируют обучающихся с высоким уровнем подготовки. Из анализа рис. 1. видно, что экспериментальные точки, характеризующие низкий, средний и высокий уровень знаний практически лежат на характеристической кривой, следовательно задание в тестовой форме №35 наиболее адекватно модели измерений. Эмпирический уровень значимости для этого задания равен 0,989.
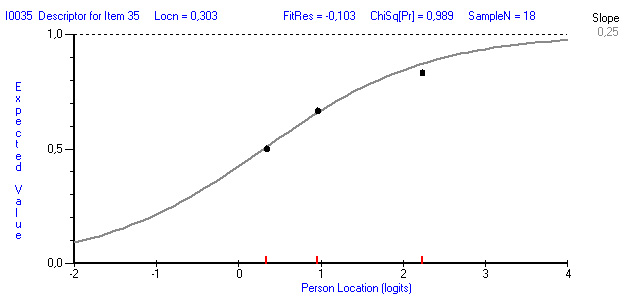
Рис. 1. Характеристическая кривая тестового задания № 35
Следующие примеры интерпретируют задания в тестовой форме как самое легкое и самое трудное задание.
Наиболее легким тестовым заданием является задание №18 «Отсутствие или степень наличия внутренних и внешних дефектов в бриллианте, называется…», трудность которого равна -1,887 логит (см. рис.2.). Рисунки с характеристическими кривыми имеют определённую структуру: по оси абсцисс отложены значения ”уровня знаний” по профессиональному модулю (в логитах). По оси ординат откладывается вероятность ожидаемого ответа индивида (Expected Score), которая варьирует от 0 до 1.
В верхней части рисунка расположена следующая информация:
– код тестового задания (I0018);
– название тестового задания (здесь названия заданий выбраны по умолчанию, в данных случаях это Descriptor for Item 18);
– мера трудности задания (Locn = -1,887);
– суммарное отклонение ответов индивидов на данное задание от ожидаемых на основе модели Раша (FitRes = -0,105);
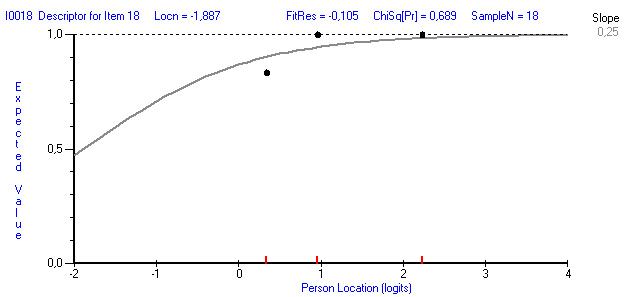
Рис. 2. Характеристическая кривая тестового задания № 18
– степень соответствия данных модели Раша (ChiSq[Pr] = 0,689);
– объем выборки испытуемых (Sample N = 18).
Характеристическая кривая наиболее трудного задания в тестовой форме: является задание № 26 «Определите, какая из предложенных типов огранок называется ступенчатой…» с трудностью 1,532 логит. Характеристическая кривая этого тестового задания представлена на рис. 3., данный пример определяет по уровню подготовленности обучающихся.
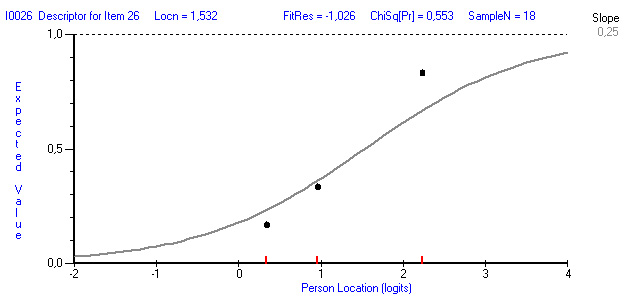
Рис. 3. Характеристическая кривая тестового задания № 26
В заключение можно сделать следующие выводы:
На основе проведённого экспериментального исследования качества заданий в тестовой форме в парадигме измерения латентных переменных можно дать многомерную содержательную оценку и получить важные рекомендации для их улучшения. Разработанные задания в тестовой форме являются достаточно эффективным, но отдельные задания нуждаются в доработке для дальнейшего использования. Это естественный процесс, поскольку процедура разработки любого теста носит итерационный характер.
Исследуемые задания в тестовой форме позволили выявить интегрированный и многомерный образовательный результат по профессиональному модулю «Изготовление вставок в ювелирные изделия», который был обработан с помощью программы RUMM 2030. Разработанная совокупность индикаторных переменных соответствует модели измерения.

