Введение
Одной из операций процесса рыболовства является постановка (выметка) орудия рыболовства. На важность изучения этой операции в своих работах указывали Ф.И. Баранов, [3]; Н.Н Виноградов, [5]; Н.Н. Андреев, [1]; В.А. Ионас, [7]; Н.В. Кокорин, [8]; Ю.Б. Артюхин и др, [2]; В.И. Сеславинский, В.Н. Аверков, [9] и другие исследователи.
До сир пор в рыболовстве исследователи уделяли большое внимание стационарным операциям: тралению с постоянной скоростью, застою яруса. Процессы постановки (выметки) и выборки орудия лова являются нестационарными, поэтому требуют дополнительных фундаментальных исследований.
Материалы и методы исследования
Исследуется процесс погружение якоря на заданную глубину с закрепленным к нему канатом, используя динамику тела переменной массы [4].
В работе используются следующие допущения:
Гидродинамические коэффициенты канатов и цилиндров зависят от материала тела и числа Рейнольдса Re[6].
При 
гидродинамические коэффициенты канатов, не зависят от числа Рейнольдса, т.е. имеет место автомодельность по Re [6, 7].
В силу того, что при погружении якоря число 
достигается в течение первых нескольких секунд, поэтому весь процесс погружения рассматривается как автомодельный по Re.
Результаты и их обсуждение
Решение задачи осуществляется в три этапа. На первом этапе исследуется погружение отдельного якоря; на втором – погружение каната, а на третьем – погружение системы «якорь- канат».
Так как якорь движется поступательно, то он рассматривается как материальная точка. Уравнение движения якоря имеет вид:
, (1)
где Ma- масса якоря; V- скорость якоря; 
- вес якоря в воде; 
- коэффициент веса якоря в воде; 
- гидродинамическая сила; 
- коэффициент гидродинамической силы якоря; p- плотность морской воды; Sa - характерная площадь якоря.
Для уравнения (1) решается задача Коши. Начальные условия имеют вид: t0=0 (момент начала движения); z(t0)=z0 (начальная скорость); z(t0)=z0 (начальная глубина ); T- время окончания погружения якоря на заданную глубину.
Уравнение (1) запишем в форме
, (2)
где 
;
; b > 0, b < 0.
Решая уравнения (2), находим скорость погружения якоря:
(3)
Формула (3) справедлива при
, 
.
Если начальная скорость якоря равна нулю, то формула (3) принимает вид:
(4)
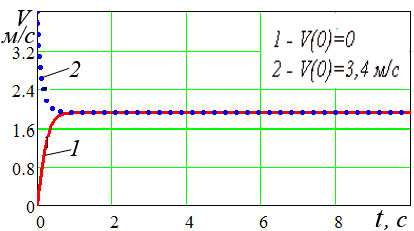
На рис.1 приведены графики зависимости скорости погружения якоря от времени при следующих исходных данных: 
; 
(бетон); Ma=45 кг.
|
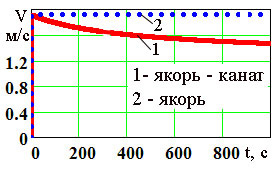
Рис.1. Графики зависимости скорости погружения якоря от времени |
Как видно с рис. 1, скорость якоря (не зависимо от величины начальной скорости) через несколько секунд достигает своего постоянного значения, равного
. (5)
Таким образом, скорость погружения якоря можно находить по формуле (4) при любых значениях начальной скорости.
Интегрируя (4), получим формулу для определения глубины погружения якоря z:
(6)
При V0=0, имеем:
(7)
Формула (7) удобна для практических расчетов глубины погружения якоря.
Ниже исследуется погружение системы «якорь – канат». Это система переменной массы. Согласно теоремы о движении центра масс, имеем:
,
где M=Ma+mz - масса системы; Ma - масса якоря; mz - масса каната. Скорость центра масс системы «якорь - канат» определяется из формул:
; 
.
Уравнение движение центра масс системы «якорь-канат» имеет вид:
(8)
где 
- вес якоря в воде; 
- вес каната в воде; Ra, Rk - гидродинамические силы якоря и каната.
Запишем уравнение (8) в нормальной форме (форме Коши):
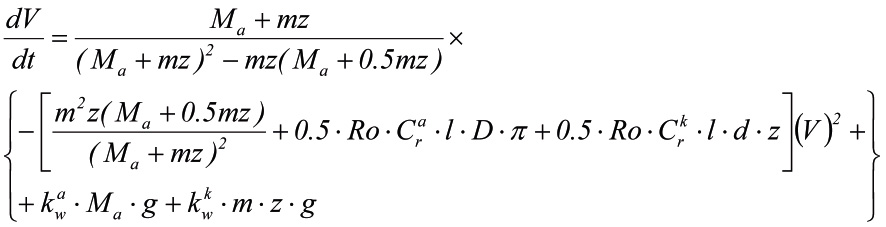(9)
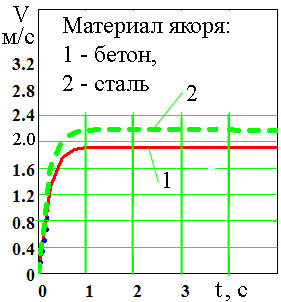
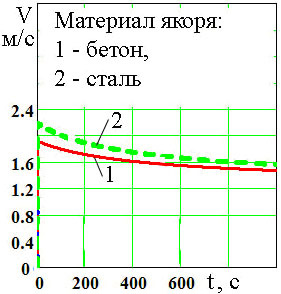
Уравнение (9) решалось численно методом Рунге-Кутта. На рис. 2 приведены зависимости, полученные его численным решением.
Для вычислительного эксперимента использовался канат из полиэстера ( диаметр d=00,1 м, линейная плотность, m=00,7 кг/м, коэффициент веса в воде 
, гидродинамический коэффициент 
) и якорь (диаметр штока Da=0,1, м; масса Ma=45 кг).
|
а) начало погружения |
б) весь период погружения |
|
Рис. 2. Зависимости скорости (V - м/с) погружения канатов от времени |
|
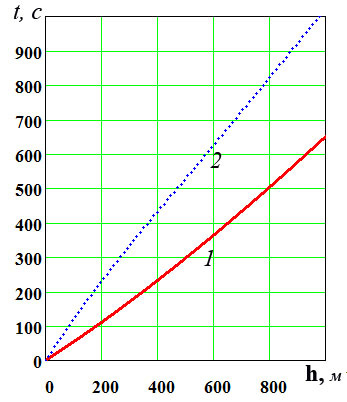
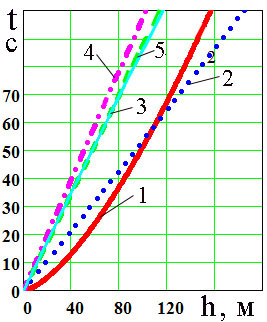
На рис. 3 показана зависимость времени погружения якоря с канатом от глубины. Рис. 4 показывает сравнительные характеристики зависимости скорости погружения системы "якор-канат" (линия 1) и якорь (линия 2).
|
Рис.3. График зависимости времени погружения системы «якор-канат» от глубины: 1- стальной якорь; 2 - якорь из бетона. |
|
Рис.4. Скорости погружения: 1 - якоря с канатом; 2 - якоря |
Ниже выполнено сравнение полученных результатов с данными Ф.И. Баранова [3] и В.А. Ионаса [7]. Формула Ф.И. Баранова имеет вид:
(10)
где q- загрузка нижней подборы невода (вес грузил в воде), Н/м; h –глубина погружения, м.
При погружении уреза невода, В.А. Ионас [7] учитывал силу сопротивления, которая уравновешивается силами веса невода в воде и силами инерции. Ионас предлагает время погружения уреза определять по формуле:
(11)
где A - коэффициент пропорциональности; h - глубина погружения; p- плотность воды; d - диаметр уреза; q - вес уреза в воде.
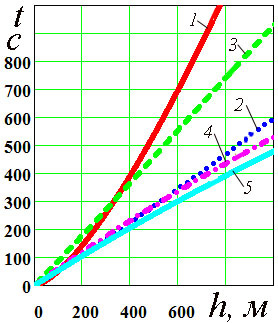
На рис. 5 приведены графики зависимости времени погружения от глубины, полученные по формуле Ф.И. Баранова (10) и системы "якорь-канат". Кривая 1 получена по формуле Ф.И. Баранова. Кривая 2 получена численным решением дифференциального уравнения (9) (канат – полиэстер, якорь бетон; Ca=0.2). Кривая 3 получена численным решением дифференциального уравнения (9) (канат – полиэстер, якорь сталь; коэффициент гидродинамического сопротивления Ca =0.5). Кривая 4 получена по формуле В.А. Ионаса (11) (канат – полиэстер, якорь - бетон). Кривая 5 получена по формуле В.А. Ионаса (канат – полиэстер, якорь - сталь).
|
а) начало погружения |
б) полный период погружения |
|
Рис.5. Графики зависимостей времени погружения элементов рыболовных орудий от глубины, полученные различными исследователями |
|
Приведенный анализ показал:
а) формула (10) не учитывает силы гидродинамического сопротивления, поэтому даёт большие погрешности;
б) результаты исследований близки к данным В.А. Ионаса [7];
в) исследования коррелируют с экспериментальными данными [2]. В экспе-рименте [2] скорость погружения равна 1.4 м/c – на рис. 7 средняя скорость погружения равна 1.5 м/c.
В силу сказанного следует полагать, что предлагаемая в работе методи-ка определения времени погружении объекта (якоря с канатом) дает более точные результаты по сравнению с методиками Ф.И. Баранова и В.А. Ионаса.
Выводы
В работе развиты теоретические исследования Ф.И. Баранова [3] и В.А. Ионаса [7] по определению времени погружения элементов ярусной, лову-шечной и других рыболовных систем.
Практическое значение, полученных результатов заключается в сле-дующем:
1.Предложенные математические модели позволят более точно оценивать временные интервалы погружения элементов яруса.
2.Избежать затрат на установку отпугивающих птиц устройств за счет под-бора материалов элементов яруса, позволяющих увеличивать скорость погружения системы.
3.Разработанные математические модели можно использования при иссле-довании динамики погружения различных орудий рыболовства.