Важность теоретического изучения задач консолидации многофазных грунтов определяется разнообразными нерешенными проблемами практики. Большое число работ посвящено нахождению решения задач в линейной постановке. Вопросам уплотнения грунтов с учетом их нелинейного закона деформирования до сих пор не уделяется должного внимания, хотя эти задачи в настоящее время являются очень актуальными. О необходимости учета этого фактора в грунтах и, в частности, в высоких земляных плотинах указывались в ряде международных конференциях и симпозиумах по реологии грунтов. Бесспорно, что одновременный учет пространственности задачи, её нелинейность, вязкие свойства уплотняемых сред, переменности физико-механических характеристик и внешней нагрузки во времени и координат дает исчерпывающий ответ вопросам исследования НДС массива, находящегося в сложных природных условиях. В связи с этим в данной работе сделана попытка внедрения теории нелинейной ползучести грунтов для ограниченной области уплотнения. При этом рассматривается только так называемая физически нелинейная теория ползучести, при построении которой, определяющее соотношение заменяется нелинейным законом, сохранив здесь геометрическую линеаризацию. Это предположение, подтверждается действительным поведением многих грунтов, находящихся под действием
Для решения задач механики уплотняемых пористых сред согласно основной модели В.А.Флорина [5], необходимо совместно рассматривать уравнения, отражающие неразрывность твердой и жидкой фаз грунта
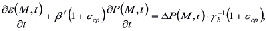(1)
состояние его скелета
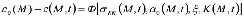, (2)
условия равновесия нестабилизированного состояния уплотняемого грунтового массива
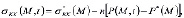(3)
где
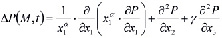; (4)
Ф – функция, отражающая состояние скелета грунта;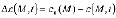 
; 
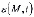- коэффициент пористости уплотняемого грунта для исследуемой точки M в момент времени t; 
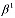- коэффициент объемного сжатия; 
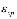- средний коэффициент пористости; P – давление в поровой жидкости; 
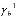- объемный вес воды; 
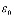- начальный коэффициент пористости;
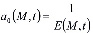
- коэффициент сжимаемости грунта;
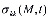- сумма главных напряжений; n – размерность рассматриваемой задачи; ξ - коэффициент бокового давления уплотняемого грунтового массива; 
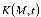- величина, которая учитывает вязкие свойства уплотняемого грунта и она зависит от выбранной математической модели состояния грунта; 
, 
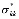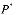- сумма главных напряжений и давление в поровой жидкости для стабилизированного состояния уплотняемого грунтового массива.
Ниже подчиняясь (1)-(3) составим ряд уравнений уплотнения многокомпонентных неоднородных и анизотропных по водопроницаемости грунтов с учетом нелинейной ползучести их скелета. Если уплотняемая земляная среда подчинена нелинейному закону деформирования, то функция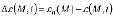 
, согласно [5] может быть представлена так:
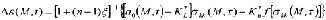(5)
Здесь
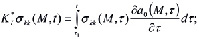
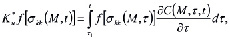
где функция f[σkk(M,τ)] отражает нелинейную зависимость между напряжениями и деформациями. Эту функцию, согласно Н.Х. Арутюняну [1] можно представить в виде степенного закона от напряжения.
C(M,τ,t)–мера ползучести грунта.
Выражение (5) можно привести и к другому виду отделив однородную часть деформирования от неоднородной части. Для этого соотношение (5) запишем так:
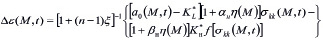(6)
Причем здесь функции a0(M,τ) и C(M,τ,t), характеризующие упругомгновенную деформацию и деформацию ползучести скелета неоднородного грунта представлены следующими математическими соотношениями:
; 
.
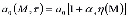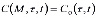
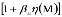Здесь η(M) - функция, зависящая от пространственных координат и отражающая неоднородность уплотняемого грунта; αн и βн параметры неоднородности, характеризующие упругомгновенную и ползучую деформацию. Соотношения (5),(6) подставив в уравнение (1) приводим его к следующему виду
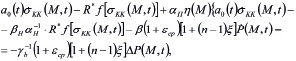(7)
где
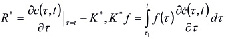
Если иметь в виду выражение (3), то уравнение (7) представляется так
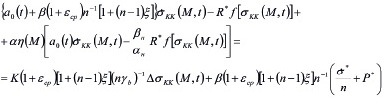(8)
Данное уравнение является нелинейным и оно составлено на основе нелинейной теории ползучести. В этом уравнении фигурирует величина f[σkk(M,τ)], являющаяся нелинейной функцией напряжения σkk(M,τ). Для выражения f[σkk(M,τ)] обычно принимают степенную зависимость. Решение полученного уравнения (8) ищем в следующем виде
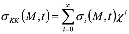(9)
Тогда решение нелинейного интегро-дифференциального уравнения консолидации сводится к определению интегралов следующей системы линейных интегро-дифференциальных уравнений
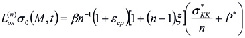; (10)
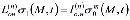; (11)
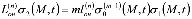; (12)
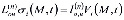, (13)
где
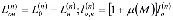; (14)
n – принимает значение 1,2,3 в зависимости от исследуемой задачи;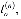 
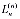- интегро-дифференциальные операторы видов
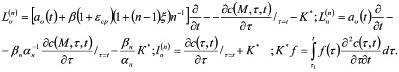(15)
Решив эту систему уравнений применительно к конкретным задачам, затем пользуясь соотношением (3) можем определить сумму главных напряжений. Эта величина в свою очередь дает возможность находить изменение давления в поровой жидкости или напора во времени и пространственных координат и определить осадку уплотняемого массива, находившегося под действием внешней нагрузки.
Система уравнений (10)-(15) при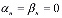 
и переменном коэффициенте сжимаемости относительно пространственных координат имеет вид
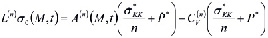; (16)
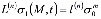; (17)
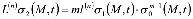; (18)
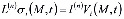, (19)
где
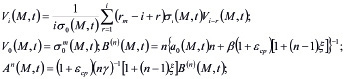(20)
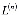- интегро-дифференциальный оператор вида
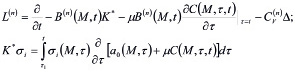(21)
Данная система уравнений соответствует состоянию уплотняемого массива, когда зависимость между суммой главных напряжений и коэффициентом пористости представляется нелинейным
Если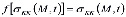 
, то уравнение (8) относительно порового давления P(M,t) имеет вид
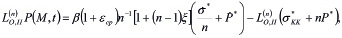(22)
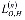- тот же интегро-дифференциальный оператор, приведенный в (11).
Выражение (22) является уравнением консолидации неоднородно-наследственно-стареющих грунтов, коэффициент фильтрации которых различны в трех взаимно перпендикулярных направлениях.
Решение уравнения (22) находим при помощи метода возмущений, успешно применяемого в теории упругости неоднородных тел [6]. Согласно этому методу введем малый параметр χ следующим образом
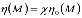, (23)
где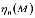 
- некоторая непрерывная функция.
Тогда решение уравнения (22) можно представить так
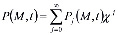. (24)
Здесь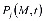 
- некоторая неизвестная непрерывная функция подлежащая определению.
Для определения этой функции выражения (23) и (24) подставим в (22), затем приравнивая коэффициенты правой и левой части полученного равенства находим следующую систему уравнений
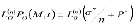; (25)
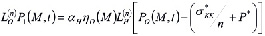; (26)
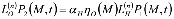; (27)
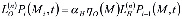(28)
Решив систему (25)-(28) при соответствующих начальных и граничных условиях находим неизвестные функции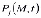 
, которые подставив в (24) получим расчетную формулу для определения давлений в поровой жидкости, зависящего от пространственных координат и времени.
Если же использовать вместо функции Ф, линейную зависимость, то уравнение консолидации (8) можно привести к виду
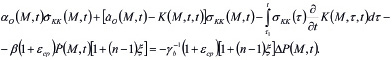(29)
Здесь K(M,τ,t) - ядро ползучести и оно является основной характеристикой уплотняемой среды; В (29) σKK(M,t) заменив его значением через поровое давление Р имеем
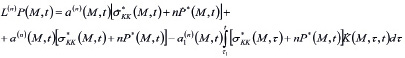(30)
где
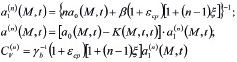
Полученное интегро-дифференциальное уравнение является уравнением консолидации анизотропных по водопроницаемости неоднородных грунтов, где учитывается линейная ползучесть.
Таким образом, все уравнения консолидации получены в неявной форме по отношению к ядру ползучести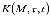 
. В зависимости от 
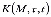естественно эти уравнения будут иметь различный вид.
Если в уравнении (8) примем
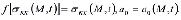
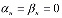и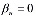 
, 
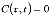, то находим такое уравнение, которое описывает уплотнение неоднородных двухкомпонентных упругих грунтовых массивов, т.е.
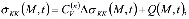(31)
где
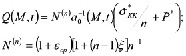
Уравнение (29) для неоднородного грунта при различных краевых условиях решено в [2-4,6].
Таким образом, получен ряд уравнений консолидации неоднородных многокомпонентных упругих и упругоползучих грунтов при их линейном и нелинейном деформировании. Они в дальнейшем будут решены для различных задач консолидации, имеющих теоретическое и практическое значения в механике уплотняемых пористых сред.