Как известно, изучение общей проблемы синтеза нелинейных динамических систем в ряде ситуаций существенно упрощается, если их рассматривать с позиций операторного подхода, и попадающих в общую схему так называемых H-операторов, действующих в пространствах сигналов. Модельными примерами могут служить нелинейные многомерные системы обработки информации, содержащие интегральные операторы Гаммерштейна, Урысона, интегростепенные ряды Вольтерра-Пикара[1].
Качественные методы решения задач синтеза этих систем приводят к нелокальной разрешимости соответствующих операторных уравнений в исходных функциональных пространствах как внешней среды.
Задача синтеза сводится к формированию оптимальных программных и стабилизирующих управлений, построению алгоритмов обработки входных наблюдений и структурных схем оптимальных приемников, линейных и нелинейных фильтров, обнаружителей сигналов в рамках заданных критериев качества при наличии возмущений различной природы.
Существенным фактором при синтезе любой системы автоматического регулирования и управления является чувствительность системы к изменениям ее параметров. Одними из наиболее ранних работ по чувствительности систем с обратной связью явились работы Г. Боде и Дж. Траксела [2, 3].
Ими было показано, что синтез нелинейной системы, как правило, представляет собой некорректную задачу в заданной паре линейных топологических пространств из-за нарушения порога чувствительности и больших значений числа обусловленности в структуре динамической матрицы системы с заданными собственными свойствами [4].
Представляет большой интерес решение следующих задач, связанных с синтезом нелинейных динамических систем:
Задача А. Построить по заданному уравнению (системе уравнений) такое пространство, которое сводило бы качественную картину исходного процесса к такой, в которой оператор задачи обладал бы нужными для исследователя свойствами: являлся непрерывным, компактным, сжимающим, вполне непрерывным, дифференцируемым и так далее.
Задача В. Найти интегральное или псевдоинтегральное представление Н-оператора в заданной паре локально невыпуклых топологических пространств.
Задача С. Проинтерполировать хотя бы некоторые из свойств нелинейного Н-оператора для локально невыпуклых топологий.
Задача D. Использовать качественные (в частности, топологические) методы современного нелинейного функционального анализа при решении операторных уравнений и их систем, с входящими в них Н-операторами.
Задача Е. Детально исследовать структуру и геометрию L-характеристики нелинейного Н-оператора в паре локально ограниченных функциональных пространств.
В частности, к настоящему времени есть некоторое продвижение результата М. Рисса об интерполяции линейного оператора в случае нормированных и локально выпуклых пространств в работах И Шапиро, А. Дейч, П. Жирарде, А. Фавини, П. Крэ, В.А. Винокурова, однако для пространств, не являющихся локально выпуклыми, вопрос остается открытым.
Становление и развитие данной тематики было связано как с отечественными школами функционального анализа: санкт-петербургской (А.В. Бухвалов, Г.Я Лозановский и др.), московской (О.В. Бесов, В.И. Буренков, М.Л. Гольдман и др.), новосибирской (А.Г. Кусраев, С.С. Кутателадзе и др.), воронежской (М.А. Красносельский, С.Г. Крейн, Е.М. Семенов и др.), ростовской (Ю.Ф. Коробейник, М.М. Драгилев, С.Г. Самко, В.П. Захарюта), так и с зарубежными школами: голландской (В.А. Люксембург, А. Шепп, А.С. Заанен и др.), польской (В. Орлич, Ю. Муселяк и др.), германской (Х.Й. Трибель, Ю. Аппель и др.).
Первому автору настоящего доклада принадлежат результаты об интерполяции линейных мажорируемых операторов в модулярных (в общем случае небанаховых) пространствах Орлича аналитических функций и решеточных квазинормированных пространствах Орлича.
Примерами интерполяционных топологий могут служить локально ограниченные функциональные пространства Лебега 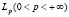 , модулярные пространства Орлича L*φ (в случае φ-функции, подчиняющейся Δ2-условию как в вещественном, так и в комплексном случаях), пространства Харди Hp и так далее.
, модулярные пространства Орлича L*φ (в случае φ-функции, подчиняющейся Δ2-условию как в вещественном, так и в комплексном случаях), пространства Харди Hp и так далее.
Обобщению интерполяционных теорем М. Рисса и И. Марцинкевича на другие семейства банаховых и метрических пространств был посвящен ряд работ А.П. Кальдерона, А.Зигмунда, Я.Б. Рутицкого, Е.И. Пустыльника, П.П. Забрейко, Г.Я. Лозановского, Е.М. Семенова, Ю.И. Петунина, С.Г. Крейна и другие.
Нами была построена двумерная шкала модулярных пространств Орлича измеримых по Лебегу функций и установлены результаты об интерполяции полилинейного оператора в этой шкале.
Наиболее важными в приложениях являются нелинейные динамические системы, относящиеся к следующим двум типам:
– динамические системы – системы, с изменяющимся с течением времени состоянием. Наибольшее увеличение сложности вносит стремление системы к устойчивому неравновесному состоянию. Также сложность повышается, если процессы, происходящие в системе, имеют колебательный характер. Из всех существующих видов динамических систем особо сложными являются дискретные динамические системы;
– системы с алгоритмической записью информации. Здесь алгоритмическая сложность – длина самого короткого способа записи конечной последовательности знаков. Наиболее сложной алгоритмической записью является описание случайного процесса.
Целесообразно отметить [5], что выбор того или иного пространства в качестве внешней среды является определяющим для конкретного метода синтеза закона управления. В настоящее время при операторном подходе к синтезу нелинейных динамических систем наиболее употребительными являются локально ограниченные пространства Лебега и Орлича.
В соответствии с общепринятой символикой, означает поле вещественных чисел,
+ = {x∈| x ≥ 0} – поле вещественных неотрицательных чисел, – кольцо натуральных чисел, n – линейное n-мерное евклидово пространство, – пространство вещественно значных функций, дифференцируемых не менее, чем k раз, (k ≥ 1), а М – пространство всех измеримых по Лебегу вектор-функций.
Через Lp(), (0 < p < ∞), обозначим пространство комплекснозначных функций u(t) (со значениями в l) действительного аргумента t ∈ с p-интегрируемым модулем по Лебегу, для которых:
Lp() = 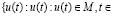 ,
, 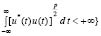 , (1)
, (1)
где u*(t) – эрмитово сопряженная функция к исходной измеримой функции u(t) ∈ M.
Заметим, что исходное пространство
Lp() является локально ограниченным, причем при p ≥ 1 оно представляет собой банахово (полное нормированное) пространство, а при 0 < p < 1 является локально невыпуклым.
Через L∞() (где p → ∞) обозначим пространство, обусловленное формулой вида:
L∞() = 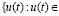 l, t ∈ ,
l, t ∈ , 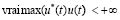 , ∀t ∈ }, (2)
, ∀t ∈ }, (2)
где
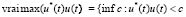 почти всюду на , ∀t∈. (3)
почти всюду на , ∀t∈. (3)
F-норма элемента u(t)∈L∞() определяется по формуле:
||u; L∞() ||= 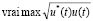 , ∀t∈. (4)
, ∀t∈. (4)
В случае векторных и матричных комплекснозначных функций пространства Лебега
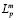 (),
(), 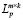 (),
(), 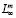 (),
(), 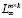 () и нормы в них задаются аналогичными формулами [3] (c. 396, 397), поэтому, для краткости изложения их опускаем.
() и нормы в них задаются аналогичными формулами [3] (c. 396, 397), поэтому, для краткости изложения их опускаем.
Для бесконечномерного случая можно использовать нашу монографию [4] (c. 20-30), где рассмотрен ряд нетрадиционных примеров локально ограниченных пространств.
В данной статье мы обсуждаем возможность использования в качестве внешней среды для указанных систем более широкого семейства локально ограниченных функциональных пространств Орлича.
Обозначим через (Ω, Σ, μ) пространство с мерой, где Ω – компактное множество в , Σ–σ – алгебра всех его измеримых подмножеств, μ – σ – аддитивная мера (для простоты μ можно считать мерой Лебега).
Пространство Орлича L*Ф состоит из измеримых по Лебегу функций, определенных на (Ω, Σ, μ), и порождается неотрицательной неубывающей функцией Юнга Ф, обладающей рядом свойств. В частности, если рассматриваются измеримые вектор-функции 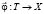 , где X – нормированное В-пространство, то естественно считать, что порождающая ЛОФП функция Юнга Ф определена на Х.
, где X – нормированное В-пространство, то естественно считать, что порождающая ЛОФП функция Юнга Ф определена на Х.
Если же функция Юнга Ф определена на промежутке [0, ∞), то тогда в определении пространства Орлича L*Ф непосредственно участвуют не значения 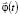 самих вектор-функций
самих вектор-функций 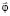 , а их нормы в исходном пространстве Х. Очевидно, такой подход сводится к предыдущему с помощью замены функции Юнга Ф на
, а их нормы в исходном пространстве Х. Очевидно, такой подход сводится к предыдущему с помощью замены функции Юнга Ф на 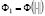 , (например, если
, (например, если 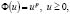 то
то 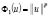 и
и 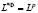 [5].
[5].
Обозначим через Ф(x, y) – произвольную седловую функцию Юнга, через ГФ(x, y) – интегральный модуляр, определяемый функцией Юнга Ф, L*Ф(Ω, Σ, μ) – локально ограниченное F – квазинормированное пространство Орлича, где
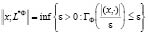 ,
,
(аналогично для элемента y). В частности, если вогнуто-выпуклая седловая функция 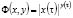 , где 0<y(τ)<1, то получим соответствующее полуупорядоченное локально невыпуклое топологическое пространство (определяемое интегральным модуляром
, где 0<y(τ)<1, то получим соответствующее полуупорядоченное локально невыпуклое топологическое пространство (определяемое интегральным модуляром 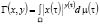 ), структура которого к настоящему времени практически не изучена, хотя решение соответствующих прикладных задач представляет определенный интерес для оценок двойственного зазора в теории невыпуклого программирования для адаптивных нелинейных динамических систем (см. подробнее [6]).
), структура которого к настоящему времени практически не изучена, хотя решение соответствующих прикладных задач представляет определенный интерес для оценок двойственного зазора в теории невыпуклого программирования для адаптивных нелинейных динамических систем (см. подробнее [6]).
Пусть φ – точный нормальный полуконечный след на алгебре Дж. фон Неймана M, K(M, φ) – (*) – алгебра всех измеримых операторов, присоединенных к M. Через E обозначим линейное подпространство в K(M, φ) с F-квазинормой 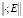 . Тогда Е представляет собой неассоциативное локально ограниченное пространство. Природа пространства Е также мало изучена, о чем свидетельствуют лишь отдельные публикации в мировой печати (см. подробнее [7]).
. Тогда Е представляет собой неассоциативное локально ограниченное пространство. Природа пространства Е также мало изучена, о чем свидетельствуют лишь отдельные публикации в мировой печати (см. подробнее [7]).
Обозначим через LФ класс всех μ-измеримых почти-периодических функций x(τ), таких, что на каждом интервале длины 2Т конечен верхний предел 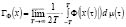 .
.
Тогда соответствующее ЛОФП, обозначаемое МФ с F-квазинормой 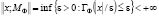 , является локально невыпуклым пространством Марцинкевича-Орлича, служащим базовым для синтеза почти-периодических систем.
, является локально невыпуклым пространством Марцинкевича-Орлича, служащим базовым для синтеза почти-периодических систем.

