Функционирование предприятия возможно при наличии информации, необходимой для выработки и реализации управленческих решений. Информация на предприятии образует информационные потоки входной информации, выходной информации и обратной связи.
Входная информация для предприятия делится на внешнюю и внутреннюю. Внешними по отношению к учреждению являются, в частности, сведения об указах вышестоящих организаций, о финансово-кредитной политике, о социальных и экономических тенденциях государства. Внутренняя информация характеризует функционирование учреждения: финансы, структуры, трудовой коллектив, материалы, оборудование, здания и сооружения. Выходные данные могут быть выражены в форме различных управляющих воздействий (решений), направленных на управляемую систему. Обратная связь пополняет внутреннюю информацию в процессе функционирования учреждения и обеспечивает корректировку отклонений от плана (идеала, эталона).
Следовательно, в современных условиях функционирования предприятия информация становится самостоятельным фактором для эффективного управления им. Этому способствует применение компьютеров для сбора, передачи, обработки и хранения информации, что привело к появлению информационных компьютерных технологий, которые позволяют руководителю: 1) ориентироваться на более глубокий анализ ситуаций для принятия решений, 2) рассматривать технологии выработки и принятия решений во всей их полноте, 3) в процедурах принятия решений перейти от «жёстких» математических моделей к «мягким» моделям, в которых формальные вычисления комбинируются с экспертными оценками, 4) активнее использовать инновационные технологии прогнозирования, стратегического и тактического планирования, 5) повысить внимание к организационной и психологической стороне применения математических и вычислительных средств в процессах принятия решения [1–4].
Информационно-компьютерные технологии помогают лицу, принимающему решения, на этапах сбора, отбора, анализа и целевой обработки информации. Для информационной поддержки на этом этапе используются компьютерные системы, называемые системами поддержки принятия решений (СППР), которые можно представить в виде
М = {S, R, I, K},
где S – база имитационных моделей, R – база продукционных правил, которая пополняется в результате анализа принятия решений в сложных ситуациях, I – информационная база, K – база общих знаний. Основные этапы разработки информационно-компьютерной СППР в учреждении состоят в следующем: 1) определение основных составляющих и условий функционирования учреждения; 2) анализ закономерностей и эмпирических данных о структуре и особенностях экономических, социальных и экологических рисков; 3) анализ и систематизация источников информации и информационных потоков; 4) разработка методов принятия решений и математических моделей в условиях неполной информации и при наличии ограничений; 5) разработка спецификации, интерфейса и структуры информационно-компьютерной СППР; 6) реализация и тестирование информационно-компьютерной СППР.
Руководителю бюджетной организации целесообразно иметь пакет прикладных программ (ППП) для поддержки принятия решений по актуальным задачам ее функционирования Настоящая работа является еще одной компонентой такого ППП в дополнение к ранее опубликованным работам [5], [6].
Постановка задачи.[1] Допускаем, что задан или отработан требуемый (идеальный) процесс изменения критериев эффективности функционирования предприятия во времени: это математическое описание управленческого решения. Имеется реальный процесс изменения тех же критериев, отличающийся от идеального, и заданный другим математическим описанием. Задача заключается в таком управлении наблюдаемым реальным процессом изменения критериев путём денежных вложений в структуры предприятия, при котором разница между реальным и идеальным процессами изменения критериев будет минимальной в каждый момент времени, определяемый планом контроля величин критериев.
Математическое описание. Полагаем, что корректно решена задача идентификации реального процесса и он адекватно отражён матричным дифференциальным уравнением
, 
, 
,
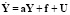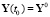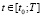где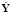 
– производная по времени от матрицы Y; a – матрица размера 
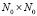взаимозависимостей критериев эффективности; U – матрица размера 
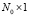, компонентами которой являются подлежащие определению управления; f – матрица размера 
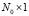вида
,
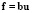где b – матрица размера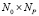 
коэффициентов влияния денежных вложений в расходные структуры предприятия на критерии эффективности; u – матрица размера 
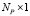, компонентами которой являются относительные денежные ресурсы, вкладываемые в расходные структуры предприятия.
Наблюдаемые переменные Z реального процесса связаны с переменными состояния Y зависимостью
,
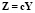где с – матрица размера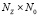 
.
Полагаем, что идеальный процесс адекватно задан матричным дифференциальным уравнением – это математическое описание управленческого решения:
, 
, 
,
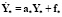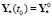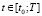где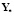 
, 
, 
, 
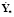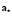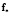– матрицы, имеющие те же размеры и тот же смысл, что и соответственно матрицы Y, 
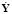, a, f в первом уравнении, но отличающиеся от последних своей «идеальностью», реализуя требуемое изменение критериев эффективности во времени; 
, 
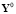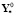– начальные условия для матриц Y, 
; 
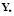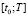– интервал времени, на котором осуществляется управление процессом. Наблюдаемые переменные 
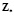идеального процесса связаны с переменными состояния 
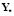зависимостью
.
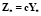Очевидно, что разность наблюдаемых переменных реального и идеального процессов определяется зависимостью
.
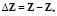Критерий оптимальности, путём минимизации которого определяется управление U реальным процессом, имеет вид
,
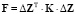где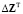 
– транспонированная матрица от матрицы ΔZ, K – матрица размера 
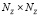весовых коэффициентов критерия оптимальности, которыми можно выделять значимость той или иной компоненты разности ΔZ. Таким образом, компоненты Uj управления U определяются на основе реализации процедуры
, 
.
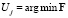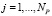Подставив выражения для Z и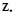 
в выражение для ΔZ, получим
.
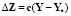Введём обозначение
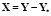
и перепишем выражение для ΔZ
.
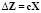Вычитая из уравнения для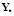 
уравнение для Y, получаем:
,
.
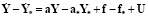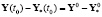Прибавляя и вычитая в правой части этого уравнения слагаемое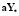 
, получаем эквивалентное уравнение
,
.
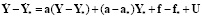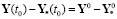Введём обозначения:
, 
, 
,
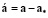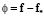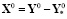использовав которые, перепишем предыдущее уравнение
, 
, 
.
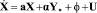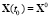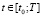Подставив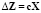 
и 
в выражение для F, получим
.
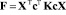Введём обозначение для матрицы размера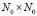 
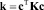
и перепишем предыдущее выражение
.
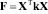Алгоритм решения задачи включает в себя следующие действия:
0: задать:
0.1: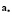 
, 
, 
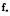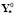– характеристики идеального процесса;
0.2: a, f,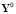 
– характеристики реального процесса;
0.3: с – матрица связи наблюдаемых переменных с переменными состояния;
0.4: К – матрица весовых коэффициентов критерия;
0.5: t0 , T – начальный и конечный моменты времени управления процессом;
1: t = t0 и вычислить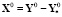 
, 
;
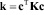2: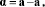 
, 
;
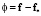3: проинтегрировать матричное уравнение (4) на шаге решения по времени;
4: проинтегрировать матричное уравнение (15) на шаге решения по времени;
5: вычислить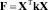 
;
6: реализовать процедуру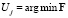 
, 
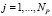, в результате чего получить в текущий момент времени управление, которое полагаем на шаге решения постоянным;
7: вывести t, U;
8: замкнуть цикл по времени, осуществляя приращение текущего момента времени на величину шага решения и операцию сравнения текущего момента времени с конечным моментом времени.
Можно показать, что для одномерного частного случая, в котором реальный процесс описывается дифференциальным уравнением
, 
, 
,
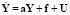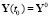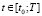идеальный процесс описывается дифференциальным уравнением
, 
, 
,
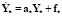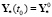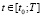зависимости наблюдений имеют вид
, 
,
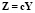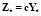критерий оптимальности задан в виде
,
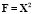где a,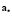 
, f,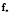 
– постоянные величины, уравнения имеют аналитические решения и алгоритм решения задачи для этого частного случая представляет собой следующие операции:
0: задать:
0.1: a, f,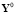 
– параметры реального процесса;
0.2: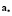 
, 
, 
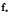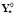– параметры идеального процесса;
0.3: t0, T, Δt – параметры времени;
1: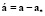 
, 
, 
;
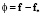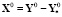2: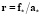 
;
3: t = t0;
4: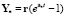 
;
;
;
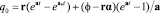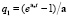5: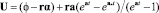 
;
6: вывести t, U;
7: t = t + Δt;
8: если t < T, то идти к 4;
9: закончить.
На основе этого алгоритма разработана программа, которая решает поставленную задачу для частного случая. Анализируя результаты решения, руководитель предприятия принимает окончательное управленческое решение по вложению средств в структуры этого предприятия.
[1]Постановка задачи согласована с Механовым Д.С.