Приложенными силами к частице материала, перемещающейся винтовой поверхностью по плоскости, будут: G = mg – сила тяжести, Н; N2 – нормальная реакция поверхности плоскости, Н; N1 – нормальная реакция элемента винтовой поверхности, Н; f2N2 – сила трения частицы о поверхность плоскости, Н; f1N1 – сила трения частицы об элемент винтовой поверхности, Н. Частица, для общего случая горизонтального расположения оси винтовой поверхности имеет движение, описываемое дифференциальными уравнениями:
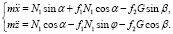(1)
Вектор абсолютной скорости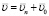 
, где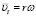 
– переносная скорость; 
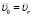– относительная скорость скольжения по винтовой поверхности определяется по формуле.
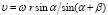, (2)
где w – угловая скорость вращательного движения винта, с-1; α – угол наклона винтовой линии к плоскости поперечного сечения, рад; β – угол между вектором скорости и осью x, рад.
Вычисления, основанные на методах Рунге-Кутта, Адамса, А. Крылова, с применением ЭВМ, показывают, что период неустановившегося движения в винтовых устройствах является кратковременным, и уже по истечении нескольких секунд движение становится устойчивым, с постоянными значениями средней осевой скорости и абсолютной угловой скорости вращательного движения. Система (1) при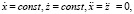 
m = 1, G = mg = 1g = g, принимает вид:
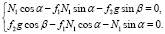(3)
Реакция N1 находится из первого уравнения :
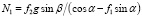. (4)
Исключая N1 из системы уравнений, получим:
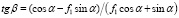. (5)
Уравнение (17) позволяет выявить для каждого данного устройства с рабочим органом в виде винтовой поверхности такое положение транспортируемой массы, определяемое значением угла β, при котором вектор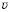 
будет располагаться параллельно оси рабочего органа.