The nontraditional conjugate vectors (tangent and cotangent) of the finite Euler rotation are proposed to be used in the problem of Euler rigid body (RB) dynamics. Moduli of these vectors are proportional to tangent and cotangent of a quarter angle of rotation. Contrary to the classical Rodrigues’ vector, they do not become infinite within the complete RB rotation. Kinematic differential equations for these vectors have common solution (in the Cauchy’s form). New dynamic polar differential equations are obtained from the classical dynamic Euler-Poisson equations as a result of replacement of angular velocity vector by the vector kinetic moment, as well as replacement of three directional Poisson cosines by the conjugate vectors coordinates. In the case of Euler, three obtained scalar dynamic differential equations have two classical first integrals (of energy and areas). Three new dynamic equations are considered as integrable ones. These equations explicitly determine the whole RB orientation, not just its vertical, like three Poisson equations do.
1. In classical Euler’s problem of rigid body (RB) dynamics with a fixed point [1], the differential Euler-Poisson equations are commonly used. Three Poisson equations determine only the earth vertical reference in relation to RB, not the whole RB orientation. Moreover, it is presumed possible to determine RB orientation through the Euler angles with additional integration of expression for time derivative of RB precession angle [1, page 16]. But the direct integration of only three Poisson equations basically does not solve the problem of determining RB orientation in three-dimensional space. In order to explicitly determine RB orientation, it is necessary to have at least six directional cosines. However, in this case, one must integrate nine differential equations instead of six Euler-Poisson equations. In this regard, the possibility of using well-known three-dimensional rotation vectors in RB dynamics is appealing, because they have three independent coordinates.
The classical Rodrigues’ vector [1] has modulus with tangent (tg(φ/2)) of half–angle φ of RB finite rotation. This vector cannot be used in the problem of RB dynamics for φ ≥ π. Unconventional conjugate rotation vectors considered in papers [2–4]: 
, 
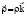, where τ = kτtg(φ/4), ρ = kρctg(φ/4) (kτ, kρ. – the arbitrary constant coefficients, 
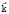– unit vector of Euler axis of RB finite rotation) are of particular interest (for 0 < φ < 2π)) by virtue of their conjugation properties [4].
New statement of Euler problem of RB dynamics is proposed in the report on the basis of differential equations for the RB conjugate rotation vectors.
2. The conjugate polar non-linear vector kinematic differential equations of RB rotation are considered in the form of linear transformations of angular velocity vector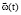 
of RB rotation (as an independent vector variable of time function) [4, 5]:
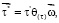
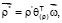(1)
where 
, 
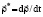are the local (relative) derived vectors with respect to time t (the derivatives with respect to some coordinate basis J, associated with RB);
τ’ = ∂τ∕∂φ, ρ’ = ∂ρ∕∂φ are the partial derivatives of the τ, ρ vectors moduli with respect to angle φ, which are defined as the following functions: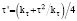 
, 
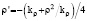; θ(τ), 
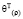are the orthogonal operators [4]: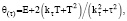 
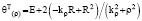, т is the transposition.
Here, T and R are the skew-symmetric operators of vector multiplication [3–5], which satisfy the identities: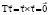 
, 
, 
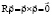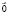is zero vector, E is unity operator. The operators θ(τ), θ(ρ) satisfy the identity (θ(τ)θ(ρ))2 = E, which determines conjugacy of the vectors 
аnd the equations (1) [5] as the properties of duality and isomorphic correspondence.
3. The equations (1) have the first (trigonometrical) integral in the form of scalar product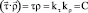 
(arbitrary constant) and allow simple and intuitive kinematic interpretation, polar precession-nutation model [5] at arbitrary vector 
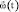аnd for any RB. In the first equation, vector 
is being transformed (at every instant of RB motion) into the vector 
by the operator θ(τ) as a result of precession 
by angle ψθτ=φ/2 (rotation of vector 
with modulus ω(t) over the surface of some circular precession cone with cone angle 2υω) around the Euler axis with unit vector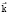 
. Angle υω – the nutation angle (deviation of vector 
from unit vector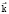 
. Then, the vector 
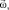is multiplied by the scalar operator τ′Е. In the second equation, the vector 
is being precessed (rotated over the same cone surface) by angle ψθρ = (π + φ/2) and is multiplied by the scalar operator ρ′Е. The nutation angle υω is determined from the scalar products: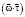 
, 
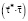or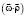 
, 
.
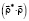On the basis of such interpretation, the equations models (1), for example, the kinematic non-holonomic equality is obtained:
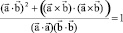(2)
where 
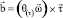. From the equality (2), follows the equality with the arbitrary constant Сτ = kτ, for example:
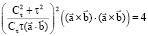(3)
The equalities similar to the equalities (2) and (3) are obtained at replacing the vector 
by the vector 
. The equations (1) have common solutions in the Cauchy form [5, 6]. So, the general solution of the first equation (1) determines the type of group multiplication and division operations of vectors 
in the associative Lie group [6]. In this group, the inverse element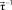 
is equal to the opposite vector, i.e. 
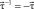, while the unity element is equal to zero vector 
.
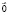4. On the basis of kinematic equations (1), the various new (polar) dynamic differential equations of RB rotation are obtained.
In the classical case of Euler, the problem of solving the system of six dynamic differential Euler-Poisson equations [1] comes to integration of system of only three dynamic equations with two independent classical first integrals (of energy and areas [1]). These two integrals are enough in order to consider the system of three equations as integrated [1].
Moreover, the change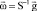 
is introduced in the equations (1), where 
is the constant vector of kinetic moment (constant in magnitude and direction in the reference basis I [1]); S–1 is the inverse operator S of RB inertia [4, 5] (constant in the basis J bound with RB).
Obtained from (1), for example, the polar matrix differential equation with coordinates of the vector 
has the following form (see also 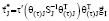[4]):
(4)
where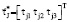 
is the column matrix with coordinates of the derivative 
in the basis J; θ(τ)J is the matrix (3×3) of operator θ(τ) in the basis J; SJ is the diagonal matrix (3×3) with three constant principal moments of RB inertia;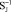 
is the inverse matrix, gI = [gi1 gi2 gi3]T is the constant column matrix with the vector 
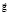coordinates in the basis I.
Three vector 
coordinates explicitly define RB orientation. In the problem of RB dynamics, in general case (at variable vector of kinetic moment), the equation (4) is used in combination with the dynamic Euler equations for the vector of kinetic moment [1].
The work is submitted to the International Scientific Conference “Modern materials and technical solutions”, London, October 18–25, 2014 came to the editorial office оn 22.10.2013.