Одним из самым парадоксальным примеров среди решений задач с пифагоровыми тройками – это решение американского изобретателю многочисленных математических и шахматных головоломок Сэма Ллойда, он решает задачу У.Лонгфелло из романа «Каванаг» по своему.
Условие из романа: цветок лотоса возвышается над поверхностью озера на 2 пяди дюймов, а максимальное отклонение равно локтю, т.е. 21 дюйму. Надо также найти глубину озера. Ответ:17,05 дюйма.
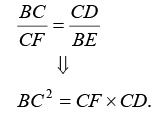
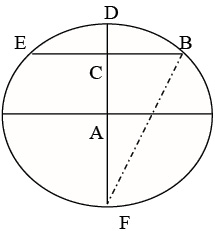
Решение С.Ллойда:
1.21×21=441
2.441:10=44,1
3.44,1-10=34,1
4.34,1:2=17,05 (дюймов).
Треугольник Лонгфелло-Ллойда имеет параметры (21; 17,05; 27,05) или умножив на 20 получим треугольник в целых числах - (341,420,541), где 341 и 541 - простые числа, а 420 кратно 60, т.е. делится одновременно на 3,4,5.
Удивительно, но эти целочисленные параметры получаются непосредственно из формул, при m=21, n=10:
a=m2-n2=212-102=341
b=2mn-2×21×10=420
c=m2+n2=212+102=541 (!).
В матрице много пустых клеток, которые являются следствием общей теоремы о пифагоровых тройках чисел.
Если m=5 и n=1, то a=24, b=10, c=26.
где (10,24,26)~(5,12,13).
Современная французская версия задачи «О лотосе» дана в книге М. Беррандо как задача «О нефтяной вышке».
Треугольник (17,21,27)
В Северном море установили на тяжелой бетонной платформе, закрепленной на дне моря, нефтяную буровую вышку. Она возвышалась над гладью воды на h=40 м. Во время сильного шторма вышка опрокинулась. Катастрофа была заснята с соседней платформы, причем было замечено, что вышка исчезла в пучине в s=84 м от точки, где прежде поднималась вышка. Чему равна глубина в этом месте?
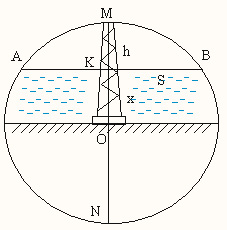
Легко заметить, что пара чисел из условия задачи (40,84) пропорциональны паре (10,21) из задачи Лонгфелло. Отсюда естественный вывод, что глубина моря, где стояла нефтяная вышка, равна: 4×17,05=68,2 (метра).
Заключение. Теорема Пифагора как фундаментальный факт обладает значительным дидактическим ресурсом обновления содержания образования в 5-6 классах, позволяющим органично связать теорему с понятием простого и составного числа, признаками делимости на 3, 4, 5, введением понятия подобия геометрических фигур в начальный курс математики 5 и 6 классов. Это может в действительности стать основой интегративного курса математики, объединяющего геометрические и алгебраические компоненты единого математического знания.
По аналогии с американской версией задачи «о лотосе» можно составить задачу о камыше.
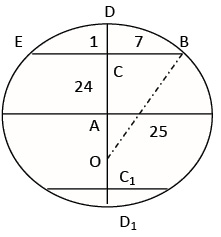
Треугольник (7,24,25)
1.7×7=49
2.49:1=49
3.49-1=48
4.42:2=24 (дм)
Алгебраически при m=7 b n=1 получим:
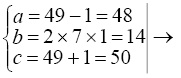(14,48,50) ~ (7,24,25)
В учебнике для 8-го класса П.М. и О.П. Эрдниевых вводится признак Пифагора (упоминался ранее в работах Мордухай-Ботовского).
Признак Пифагора:
Если a < b < c, и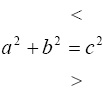 
, то Δ – тупоугольный
Δ – прямоугольный
Δ – остроугольный
Рассмотрим квазипериодическую матрицу
|
а |
b |
c |
|
|
1 |
2 |
3 |
Не существует |
|
2 |
3 |
4 |
Тупоугольный |
|
3 |
4 |
5 |
Прямоугольный (египетский) |
|
4 |
5 |
6 |
Остроугольный |
Оказывается, что (2,3,4) – это единственный тупоугольный треугольник, у которого параметры a=n-1, b=n, c=n+1.
Если у целочисленного треугольника со сторонами n-1, n, n+1 и углом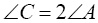 
, то такой треугольник единственный с параметрами 4,5,6.
Следует заметить, что эти целочисленные треугольники применялись томским академиком Ильиным в доказательстве теоремы Ферма для xn+yn=zn , при n ≥ 3 не имеющего целочисленного решения.