Scientific journal
International Journal of Experimental Education
ISSN 2618–7159
ИФ РИНЦ = 0,425

Personal portfolio

В рамках исследования последствий болезни паркинсона был проведен анализ авто- и кросскорреляции в стохастическом динамике динамометрических сигналов человека при болезни Паркинсона. Болезнь Паркинсона - прогрессирующее хроническое заболевание головного мозга, которое проявляется в нарушении произвольных движений.

Задачи исследования

Поиск количественных и качественных показателеи для анализа и диагностики болезни Паркинсона.

Проведение сравнительного анализа автои кросскорреляции в сигналах локомоторной активности здоровых людей и пациентов с болезнью Паркинсона.

Исследование характера изменения динамических, пространственно-временных и спектральных показателей динамометрических сигналов разных групп людей.

Для оценки степени коррелированности двух случайных величин, в математической статистике используется понятие коэффициента корреляции. Коэффициентом корреляции k(X,Y) двух случайных величин X и Y, дисперсии которых существуют и отличны от нуля, называется число:  , где cov (X,Y) - вариация случайных величин X и Y; σX σY - их среднеквадратические отклонения. При исследовании использовалась теория марковских процессов, был произведен подсчет параметра  немарковости. В качестве экспериментальных данных использованы динамометрические сигналы силы давления стопы человека на опору. В исследовании участвовали 40 волонтеров: 20 здоровых людей и 20 больных людей. На основе проведения автои кросскорреляционного анализа динамометрических сигналов здоровых людей и пациентов с болезнью Паркинсона были получены следующие результаты:

 

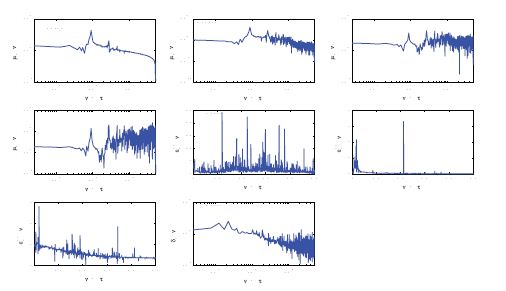
  1. Локомоторная активность здоровых людей и пациентов характеризуется разным поведением динамических, пространственно-временных и спектральных показателей динамометрических сигналов.
  2. Стохастическая динамика динамометрических сигналов здоровых людей и пациентов с болезнью Паркинсона характеризуется высокой степенью корреляций;
  3. В динамике локомоторной активности пациентов в большей степени проявляются квазимарковские (умеренные по степени проявления) эффекты, чем в случае здоровых людей.
  4. Взаимная динамика динамометрических сигналов правой и левой ног здоровых людей и пациентов отличается более сильной статистической памятью, чем в случае отдельно взятых рядов

Список литературы

  1. Yulmetyev R., Hanggi P., Gafarov F. Stochastic dynamics of time correlation in complex systems with discrete current time // Phys. Rev. E 62 (2000) 6178-6194.
  2. Goychuk I., Hanggi P. Theory of non-Markovian stochastic resonance // Phys. Rev. E 69 (2004) 021104-1-15.
  3. С.А. Демин, Р.М. Юльметьев. Немарковость, случайность (хаотичность) и самоорганизация в сложных системах живой природы. Вестник КГПУ, вып. 4, 2005.