В работе излагается обзор методов Монте-Карло, разработанных в вычислительной аэродинамике разреженного газа, и их применение в смежных, нетрадиционных для использования статистического моделирования, областях. Приводится краткая история развития методов, их основные свойства, достоинства и недостатки. Устанавливается связь прямого статистического моделирования аэродинамических процессов с решением кинетических уравнений и показывается, что современный этап развития вычислительных методов немыслим без комплексного подхода к разработке алгоритмов с учётом всех особенностей решаемой задачи: физической природы процесса, математической модели, теории вычислительной математики и стохастических процессов. Рассматриваются возможные пути развития методов статистического моделирования.
Общая схема методов Монте-Карло. Проявление методов статистического моделирования (Монте-Карло) в различных областях прикладной математики, как правило, связано с необходимостью решения качественно новых задач, возникающих из потребностей практики. Так было при создании атомного оружия, на первом этапе освоения космоса, исследовании явлений атмосферной оптики, физической химии, моделировании турбулентности. В качестве одного из более-менее удачных определений методов Монте-Карло можно привести следующее:
Методы Монте-Карло – это численные методы решения математических задач (систем алгебраических, дифференциальных, интегральных уравнений) и прямое статистическое моделирование (физических, химических, биологических, экономических, социальных процессов) при помощи получения и преобразования случайных чисел.
Первая работа по использованию метода Монте-Карло была опубликована Холлом в 1873 году именно при организации стохастического процесса экспериментального определения числа p путём бросания иглы на лист линованной бумаги. Яркий пример использования методов Монте-Карло – использование идеи Дж. фон Неймана при моделировании траекторий нейтронов в лаборатории Лос Аламоса в сороковых годах прошлого столетия. Хотя методы Монте-Карло связаны с большим количеством вычислений, отсутствие электронной вычислительной техники ни в том ни в другом случае не смутило исследователей при применении этих методов, поскольку в том и другом случае речь шла о моделировании случайных процессов. И своё романтическое название они получили по имени столицы княжества Монако, знаменитой своими игорными домами, основу которых составляет рулетка – совершенный инструмент для получения случайных чисел. А первая работа, где этот вопрос излагался систематически, опубликована в 1949 году Метрополисом и Уламом, где метод Монте-Карло применялся для решения линейных интегральных уравнений, в котором явно угадывалось задача о прохождении нейтронов через вещество. В нашей стране работы по методам Монте-Карло стали активно публиковаться после Международной Женвской конференции по применению атомной энергии в мирных целях. Одной из первых можно привести работу Владимирова и Соболя.
Общая схема метода Монте-Карло основана на Центральной предельной теореме теории вероятности, утверждающей, что случайная величина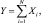 
, равная сумме большого количества N произвольных случайных величин Xi с одинаковыми математическими ожиданиями m и дисперсиями s2, всегда распределена по нормальному закону с математическим ожиданием N∙m и дисперсией N∙s2. Предположим, что нам нужно найти решение какого либо уравнения или результат какого либо процесса I. Если сконструировать случайную величину x с плотностью вероятности p(x) таким образом, чтобы математическое ожидание этой величины равнялось искомому решению M(x) = I, то это даёт простой способ оценки решения и погрешности
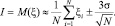
Отсюда следуют общие свойства методов:
– абсолютная сходимость к решению, как (1/N);
– тяжёлая зависимость погрешности ε от числа испытаний, как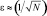 
(для уменьшения погрешности на порядок, необходимо увеличить количество испытаний на два порядка);
– основным методом уменьшения погрешности является максимальное уменьшение дисперсии, другими словами, максимально приблизить плотность вероятности p(x) случайной величины x к математической формулировке задачи или физике моделируемого явления;
– погрешность не реагирует на размерность задачи (в конечно-разностных методах при переходе от одномерной задачи к трёхмерной количество вычислений увеличивается на два порядка, в то время как в методах Монте-Карло количество вычислений остаётся того же порядка);
– простая структура вычислительного алгоритма (N раз повторяющиеся однотипные вычисления реализаций случайной величины);
– кроме того, конструкция случайной величины x, вообще говоря, может основываться на физической природе процесса и не требовать обязательной, как в регулярных методах, формулировки уравнения, что для современных проблем становится всё более актуальным.
Особое место методы Монте-Карло занимают в вычислительной аэродинамике. Динамика разреженных газов описывается известным интегродифференциальным кинетическим уравнением Больцмана
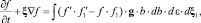
где f – f(t, x, y, z, ξx, ξy, ξz) функция распределения молекул по времени, координатам и скоростям; f′, f1′ – функции распределения, соответствующие скоростям молекул после столкновения; ξ′, ξ1′, g – относительные скорости молекул при парных столкновениях g = ξ – ξ1, ξ′ – ξ1′; b, ε – прицельное расстояние и азимутальные угол при столкновениях частиц.
Сложная нелинейная структура интеграла столкновения и большое количество переменных (в общем случае – 7) создают существенные трудности для анализа, в том числе и численного и практически исключают конечно-разностный подход для серьёзных задач. И, в тоже время, многомерность и вероятностная природа кинетических процессов создают естественные предпосылки для применения методов Монте-Карло. Исторически развитие численных статистических методов в динамике разреженных газов шло по следующим трем направлениям: использование методов Монте-Карло для вычисления интегралов столкновения в регулярных конечно-разностнных схемах решения кинетических уравнений; прямое статистическое моделирование физического явления, которое разделяется на два подхода: моделирование траекторий «пробных частиц» по Хэвиленду и моделирование эволюции «ансамбля частиц» по Бёрду; построение случайного процесса типа процедуры Уалама – Неймана, описанной в, соответствующего решению линеаризованного кинетического уравнения либо Master Equation Каца .
Вероятностная природа аэродинамики разреженных газов так важная для применения и разработки численных схем Монте-Карло естественным образом следует из общих принципов кинетической теории и статистической физики.
В книге устанавливается связь прямого статистического моделирования аэродинамических процессов с решением кинетических уравнений и показывается, что современный этап развития вычислительных методов немыслим без комплексного подхода к разработке алгоритмов с учётом всех особенностей решаемой задачи: физической природы процесса, математической модели, теории вычислительной математики и стохастических процессов. Работа выполнена при поддержке РНФ (Грант № 14-11-00709).