Учебное пособие представляет собой изложение основ статистического моделирования и приложение их к решению различных задач математики и механики. Пособие является дополнением к курсу лекции, читаемому в факультете аэромеханики и летательной техники МФТИ, может быть использовано при самостоятельном изучении. Изложение материала пособия построено таким образом, что постепенно вводит обучаемого в круг понятие нетрадиционных методов вычислительной математики. В приложении дают задачи, которые можно использовать для самоконтроля. Пособие предназначено для студентов, аспирантов, преподавателей и инженеров.
Метод Монте-Карло является численным методом моделирования широкого круга явлений и решения математических задач, связанный с получением и преобразованием случайных чисел. Создателями метода принято считать американских математиков Дж. Неймана и С. Улама в соответствии с работой 1949 г. Благодаря этой работе в науку прочно вошел термин Монте-Карло.
На основное развитие методов Монте-Карло началось с середины 50-х годов после международной конференции по мирному использованию атомной энергии работами советских ученых В.В. Чавчанидза, Ю.А. Шрейдера, В.С. Владимирова. И с этого времени советская наука прочно удерживает приоритет на мировой арене в этой новой ветви вычислительной математики, постоянно углубляя теоретические основы методой и расширяя область приложения. В настоящее время трудно называть область науки, где не использовались бы методы Монте-Карло, начиная от нужд чистой математики и кончая экономикой, медициной и военным делом. В стране был центров развития методов Монте-Карло. В Новосибирске – СО АН СССР (Г.И. Марчук, Г.А. Михайлов), в Ленинграде – ЛГУ С.М. Ермаков), в Москве – МГУ (И.М. Соболь), ИМП (В.Г. Золотухин, В.С. Владимиров), ВЦ АН СССР и МФТИ (О.М. Белоцерковский, В.Е. Яницкий), в Жуковском – ЦАГИ (М.Н. Коган, А.И. Ерофеев, В.И. Власов, Ю.И. Хлопков, С.Л. Горелов, В.А. Жаров), в Дубне и др.
Хотя теоретических основа получения надежного результата с помощью набора случайных параметров была известна давно, первая опубликованная работа по использованию метода статистических испытаний, вероятно, была работой Холла в 1873 г. по экспериментальному определению числа p. На плоскость, разлинованную параллельными прямыми, отстоящими друг от друга на расстоянии L, бросается игла длиной l ≤ L. φ – угол наклона иглы к направлению линий, у – расстояние ее нижнего конца до ближайшей сверху прямой. φ равномерно распределен на отрезке 0 и π, у – на отрезке 0 и L. Здесь ясно, что игла будет пересекать одну из линий на плоскости только тогда когда y ≤ l∙sin φ, т.е. когда соответствующая случайная точка (φ, у) попадает в область под кривой у = l∙sin φ. Еще, бросая иглу на поверхность достаточно большое число раз N, подсчитываем количество пересечений иглой линий на плоскости. Их отношение приближенно будет равно отношению площади под кривой к площади прямоугольника и будет:
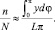
Откуда получим
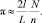
В широком смысле слова методами Монте-Карло называют основанные на моделировании случайных величин методы решения различных задач из таких областей, как статистическая физика, вычислительная математика, теория игр, математическая экономика и других.
Предположим, что случайная величина ξ определена в интервале а < x < b и имеет плотность p(x) при а < x < b. Обозначим через F(x) функцию распределения величины ξ, которая при a < x < b равна
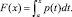
Пределы а и b могут быть бесконечные, т.е. а = –∞ и b = ∞. Можно показать, что случайная величина ξ, удовлетворяющая этому уравнению, имеет плотность распределения p(x). Действительно, так как функция F(x) монотонно возрастающая и F(a) = 0, F(b) = 1, уравнение F(ξ) = α имеет единственный корень при каждом α, при этом
P{x < x < x + dx} = P{F(x) < a < F(x + dx)}
и так как случайная величина α равномерно распределена в интервале (0, 1), то
P{x < x < x + dx} = F(x + dx) – F(x) = p(x)dx,
что и требовалось доказать.
Многие явления в природе, технике, экономике и других областях носят случайный характер, т.е. невозможно точно предсказать, как явление будет происходить. Оказывается, что течение таких явление может быть описано количественно, если только они наблюдались достаточное число раз при неизменных условиях. Так, например, нельзя при бросании монеты предсказать, выпадет «герб» или «цифра». Но если бросать монету очень чисто, то можно заметить, что отношение числа бросаний о выпадение «цифры» к общему числу бросаний мало отличается от 1/2 и тем менее откланяется от 1/2, чем больше совершено бросаний.
Случайный эксперимент, или опыт, есть процесс, при котором возможны различные исходы, так что заранее нельзя предсказать, каков будет результат. Опыт характеризуется тем, что его в принципе можно повторить сколько угодно раз. Особое значение имеет множество возможных взаимно исключающих друг друга исходов опыта.
Возможные исключающие друг друга исходы опыта называется его элементарными событиями. Множество элементарных событий обозначим E. Пример, однократное бросание игральной кости. Возможные исключающие друг друга исходы этого опыта – выпадение одного из чисел 1, 2, 3, 4, 5, 6. Множество E состоит из шести элементарных событий e1, e2, e3, e4, e5, e6, причем элементарное событие ei означает, выпадает число i.
Помимо элементарных событий, часто интересны события более сложной природы, например в случае игральной кости событие «выпадает четное число».
Пусть осуществляется некоторый опыт и пусть E – множество его элементарных событий. Каждое подмножество A ≤ E называется событием. Событие А происходит тогда и только тогда, когда происходит одно из элементарных событий, из которых состоит А.
Подмножества E, а следовательно, и само E, и пустое множество f интерпретируются, согласно общему определению, как события. Так как E состоит из всех элементарных событий, а при каждом опыте обязательно происходит одно из элементарных событий, таким образом, E происходит всегда. Такое событие называется достоверным событием. Пустое множество Φ не содержит элементарных событий и, следовательно, никогда не происходит. Такое событие называют невозможным событием.
Как правило, при использовании метода Монте-Карло моделируется случайные величины с известным законами распределения, из этих величин по заданным алгоритмам вычисляются значения существенно более сложных случайных величин, распределение которых уже не может быть найдено аналитически и используется методы математической статистики. При этом различают два подхода: параметрический и непараметрический. Параметрический подход предполагает, что искомое распределение известно с точностью до значений конечной числа параметров. Непараметрический подход используется когда параметрический вид плотности неизвестен, т.е. в тех случаях, когда информация о характере результатов либо практически отсутствует, либо имеет слишком общий характер.
Вероятная ошибка метода Монте-Карло пропорциональна √pξ/N. Скорость убывания этой ошибкой с ростом N невелика. Поэтому важно научиться выбирать для расчета интегралов такие вычислительные или другими словами, такие случайные величины ξ, для которых дисперсия Dξ по возможности будет мала. Способы построения таких схем называют методами уменьшения дисперсии, имея в виду, что для этих способ дисперсия должна быть меньше, чем дисперсия простейшего метода Монте-Карло. Работа выполнена при поддержке Российского Научного Фонда (Проект № 14-11-00709).

