Пособие основано на годовом курсе лекций, которые читаются на 3–6 курсах и в аспирантуре МФТИ. Приводятся основы метода Монте-Карло и приложения метода к различным задачам математики и механики. Излагаются основные методы решения систем линейных и нелинейных алгебраических уравнений, методы решения дифференциальных уравнений в частных производных, решение уравнений математической физики с помощью систем линейных алгебраических уравнений. Большое внимание уделяется решению задач аэродинамики (это оригинальные разработки авторов).
Быстрое развитие вычислительной техники стимулировало разработку численных методов статистического моделирования (методы Монте-Карло) широкого класса задач механики, физики, биологии, химии. Эти задачи условно можно разделить на два вида. К первому виду относятся задачи стохастической природы, когда метод Монте-Карло используется для прямого моделирования естественной вероятностной задачи. Ко второму виду относятся детерминированные задачи, описываемые вполне определенными уравнениями. В этом случае строится вероятностный процесс, математическое ожидание которого совпадает с решением соответствующего уравнения. Этот процесс численно моделируется методом Монте-Карло на ЭВМ, что позволяет получить решение в виде статистических оценок, о построение датчиков случайных чисел, о преобразовании случайных величин, о способах вычисления интегралов методом Монте-Карло, построение метода Монте-Карло для прямого статистического моделирования течений сильноразреженного бесстолкновительного газа. В данном пособий описываются способы построения методов Монте-Карло для различных уравнений, в частности, для решения систем алгебраических уравнений, дифференциальных уравнений физики, интегральных и интегродифференциальных уравнений. Рассматривается методы прямого статистического моделирования течений разреженного газа, описываемых уравнениями Больцмана, сплошносредных течений газа, описываемых уравнениями Эйлера, а также нестационарных турбулентной процессов, имеющих стохастическую природу.
Метод Хэвиленда основан на линеаризации исходной нелинейной задачи. Методы прямого статистического моделирования (Берд, Белоцерковский, Яницкий, Хлопков, Иванов, Лукшин). Недостатком метода Хэвиленда и его модификаций является то, что в его основе лежит разделение интеграла столкновения на две части, причем результат вычисления части интеграла столкновения, ответственного за убыль частиц (частота столкновения), вычисляется в предыдущей итерации, а часть интеграла столкновения вычисляется в последующей итерации, что приводит и появлению систематической ошибка в вычислении интеграла столкновений. В задачах, в которых определяющими являются процессы переноса, ошибки, возникающие в результате вычисления интеграла столкновения, мала влияют на решение задачи, и ими можно пренебречь. В случае, когда существенны релаксационные процессы, ошибки в вычислении интеграла столкновения становятся определяющими, что приводит к неверным результатам при решении соответствующих задач. Основным параметром, по которому можно судить о том, к какому классу относится та или иная задача, является параметр разреженности – число Кнудсена Kn, которое равно отношению длины свободного пробега l к характерному размеру течения L. Если число Kn > 1, то число столкновений между молекулами газа в области течения мало, по сравнению с числом столкновений молекул с поверхностью тела, и ошибки в вычислении интеграла столкновений мало влияют на результат решения задачи. В случае Kn < 1 определяющими становятся процессы столкновения молекул в газе и ошибки в вычислении интеграла столкновения приводят сначала к увеличению количества итераций, необходимых для получения решений, а затем при уменьшении числа Kn и к невозможности получения решения.
Для того чтобы можно было решать задачи при произвольном числе Kn, были предложены методы прямого статистического моделирования.
В основе методов прямого статистического моделирования лежит допущение, что реальную среду, в которой количество молекул практически не ограничено, можно заменить средой, в которой задается система из конечного числа моделирующих частиц.
Расчетная область разбивается на ячейки с линейным размером λ меньшим местной длины свободного пробега. N частиц распределяются в начальный момент времени по ячейкам в соответствии с начальной функцией распределения. Эволюцию системы за малое время Δt можно расщепить на два этапа: релаксацию подсистем в ячейках столкновения частиц и последующее передвижение всех частиц пропорционально их скорости и Δt бесстолкновительный перелет. Стационарное распределение всех параметров среды вычисляется после установления процесса во времени и усреднения по всем частицам и временным шагам.
Так, например, плотность n, скорость V, температура Т каждой ячейке на некотором шаге определяются по формулам
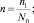
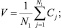
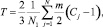
где N1 – число частиц в ячейке в момент времени t; N0 – начальное число частиц; Сj – скорость j-й частицы; m – масса частицы.
Таким образом, алгоритм методов прямого статистического моделирования состоит на двух этапов:
1 этап: столкновения частиц в ячейках,
3 этап: свободномолекулярный перенос.
Этап свободномолекулярного переноса осуществляется так жe как и в случае метода Хэвиленда, то есть частицы передвигаются из ячейки и ячейку пропорционально своим скоростям. Если обозначить конечные координаты частиц X′1, а начальные X, i = 1, ..., N, то
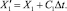
Во время этого этапа частицы могут покинуть расчетную область, столкнуться с поверхностью тела, в этом случае они отражаются от поверхности тела со скоростями, соответствующими граничной функции распределения. В момент столкновения с поверхностью вычисляются импульс и энергии, приносимые на поверхность тела. На этом этапе в области появляются частицы со скоростями, соответствующими функций распределения на внешней границе расчетной области.
Наиболее сложным для реализации в методах прямого статистического моделирования является 1 этап – столкновения частиц в ячейках. На этом этапе в каждой ячейке задана система из N частиц со скоростям C1, ..., CN. Система может переходить из одного состояния в другое только посредством столкновения частиц. Задача этапа состоит в том, чтобы найти скорости частиц через время Δt.
Отметим, что перспективность использования метода прямого статистического моделирования связана с построением кинетических моделей турбулентности, замкнутых на уровне функции распределения пульсаций. Такие модели имеют, как правило, меньше число эмпирических констант. В то же время кинетические модели более информативны, так как они дают функцию распределения пульсаций.
Данное направление интенсивно развивается, в частности, можно надеяться на успех в решении более сложных задач турбулентности, когда крупно масштабные процессы вычисляются непосредственно по схемам расщепления для конечно-разностных уравнений переноса (например, с помощью метода крупных частиц или потоков), а локальные мелкомасштабные флуктуации моделируются статистическим путем. Работа выполнена при поддержке Российского Научного Фонда (Проект № 14-11-00709).

