Учебное пособие «Сборник тестовых заданий по теории вероятностей» разработано и подготовлено к изданию на кафедре прикладной математики Уральского государственного экономического университета (УрГЭУ) кандидатами педагогических наук, доцентами Боярским М.Д. и Гниломедовым П.И. Опубликовано в 2014 году в Издательстве УрГЭУ. Материал пособия ориентирован на обучение студентов экономических и информационных специальностей и направлений подготовки в соответствии с ФГОС ВПО.
Содержание пособия распределено по трем главам: «Основные определения, факты и формулы», «Задачи с решениями» и «Тестовые задания». Каждая глава включает разделы: «Комбинаторика», «Случайные события» и «Случайные величины». В первой главе содержатся краткие теоретические сведения из соответствующих разделов курса теории вероятностей. Во второй главе приводятся полные решения задач (более тридцати) по соответствующим темам. Третья глава (основная) состоит из сорока вариантов тестовых заданий: десять вариантов по комбинаторике, два блока по десять вариантов по случайным событиям и десять вариантов по случайным величинам. К четырем вариантам приводятся краткие решения, еще к четырем – ответы.

Обложка издания
Пособие может быть использовано для текущего и промежуточного контроля знаний, для самостоятельной работы студентов при подготовке к тестовому контролю, для самоконтроля, а также при проверке остаточных знаний студентов на старших курсах.
Отличительной особенностью пособия является то, что в нем, помимо собственно тестовых заданий, содержится теоретический материал и примеры решения задач.
Предлагаемые задания различаются по уровню сложности, в то же время поиск правильного ответа не предполагает громоздких методов решения. Чтобы найти оптимальный способ решения задачи, нужно понимать основные идеи и методы теории вероятностей, знать основные определения и формулы, уметь пользоваться ими. Рекомендуется изучить первую и вторую части пособия, а лишь затем переходить к выполнению тестовых заданий.
Значительное внимание уделено разнообразию постановок задач и содержанию тестовых заданий. Приведем примеры заданий из раздела «Случайные события», позволяющих выявить понимание обучающимися взаимосвязей различных вероятностных понятий, а также проблемы в освоении этих понятий.
Задание 1. Несовместные события являются противоположными, если в ходе реализации опыта:
а) одно из них произойдет, а другие – нет;
б) появление одного из них исключает все другие;
в) их два и хотя бы одно из них произойдет;
г) их два и все они обязательно произойдут.
Задание 2. Из урны, содержащей десять деталей, две из которых бракованные, последовательно вынимают по одной две детали. Рассматриваются события: А = {при первой выемке будет вынута стандартная деталь}, B = {при второй выемке будет вынута стандартная деталь}, С = {будет вынута хотя бы одна стандартная деталь}. Вероятности событий связаны соотношением:
а) Р(С) = Р(A) + Р(B);
б) Р(С) = Р(A) + Р(B) + Р(A)∙Р(B);
в) 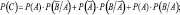
г) 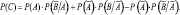
В разделе «Комбинаторика» каждый вариант заданий содержит четыре задачи, дифференцированные по уровням сложности. Такое количество и разнообразие заданий позволяет контролировать и корректировать процесс освоения обучающимися основных приемов вычисления комбинаторных величин.
1. Сколько различных трехзначных чисел можно составить из цифр 0, 2, 3, 5, 7, если цифры не повторяются?
а) 48;
б) 60;
в) 96;
г) 120.
2. Сколькими способами могут быть распределены три призовых места среди десяти соревнующихся?
а) 48;
б) 120;
в) 720;
г) 840.
3. В цветочном киоске имеются четыре розы, пять хризантем и восемь гвоздик. Покупатель просит подобрать букет из трех цветков одного вида. Сколькими способами можно составить такой букет?
а) 51;
б) 70;
в) 140;
г) 210.
4. Из группы, состоящей из семи мужчин и четырех женщин, нужно выбрать шесть человек так, чтобы среди них было не менее двух женщин. Сколькими способами это можно сделать?
а) 371;
б) 210;
в) 143;
г) 462.
Ряд заданий раздела «Случайные события» имеет целью проверить умение точно производить вычисления вероятностей.
Задание 3. В коробке находятся двенадцать шаров, из них два черных и десять белых. Наудачу вынимаются два шара. Вероятность того, что оба шара будут черными, равна:
а) 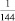 ;
;
б) 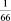 ;
;
в) 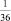 ;
;
г)  .
.
Задание 4. Для контроля продукции из трех партий деталей равных объемов взята для испытания одна деталь. Найти вероятность того, что эта деталь бракованная, если в одной партии 25 % бракованных деталей, а в двух других по 5 % брака.
а) 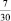 ;
;
б) 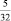 ;
;
в) 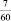 ;
;
г)  .
.
Тестовые задания по теме «Случайные величины» содержат как чисто вычислительные моменты, так и графические.
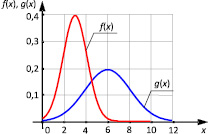
Задание 5. Даны графики плотностей f (x) и g(x) нормальных распределений двух случайных величин ξ и h соответственно. Найти математическое ожидание случайной величины ξ.
а) 1;
б) 2;
в) 3;
г) 6.
Задание 6. По данным задания № 5 определить, с какой вероятностью случайная величина h будет меньше шести?
а) 0,1;
б) 0,2;
в) 0,5;
г) 0,9.
Пособие положительно оценено рецензентами: кафедрой высшей математики и физики» Уральского технического института связи и информатики Сибирского государственного университета телекоммуникаций и информатики и кандидатом физ.-мат. наук, доцентом, старшим научным сотрудником Института математики и механики УрО РАН В.Л. Розенбергом.

