В наших работах [1, 2, 3] раскрыты некоторые аспекты взаимосвязи таких областей деятельности человека как математика и спорт, отстоящие, на первый взгляд, столь далеко друг от друга.
Первое, что осознается всеми, это связь математики и шахмат. Выдающийся математик Годфри Харди, проводя параллель между этими видами человеческой деятельности, заметил, что решение проблем шахматной игры есть не что иное, как математическое управление, а игра в шахматы – это как бы «насвистывание математических мелодий».
Связь математики и игры на бильярде можно подчеркнуть таким высказыванием: игра на бильярде – это сочетание логики, геометрии и движения.
Подчеркивает связь математики и такого вида спорта как теннис известное высказывание: «В теннис играют руками, а выигрывают головой». Опытный теннисист к сказанному добавил бы: «Для игры в теннис высокого класса необходимы три составляющие: выносливость стайера, быстрота спринтера и стремительное мышление шахматиста, безошибочно играющего в глубоком цейтноте».
Различное использование математических методов в тренерской работе позволяет существенно улучшить как индивидуальные спортивные показатели, так и результативность командных игр.
Неоспорима ценность внедрения компьютеров в область физической культуры и спорта. Математические и мультимедийные модели выступают в качестве инструмента исследования, преобразования и имитации сложных систем и динамических процессов в различных областях деятельности человека, в том числе и в спорте.
В наших работах [2, 3] мы показали, что средством ознакомления учащихся с различными аспектами использования математики в спортивной сфере, могут служить контекстные задачи, фабула которых использует данные из спортивной тематики.
В данной статье мы рассмотрим пример такой контекстной задачи, которая связана с поиском на футбольном поле наиболее выгодных точек для удара по воротам.
Задача. Футболист движется к воротам параллельно боковой линии прямоугольного поля на расстоянии 20 метров от нее (рис. 1). Он хочет нанести удар по воротам в тот момент, когда ворота будут видны под максимально возможным углом. На каком расстоянии от лицевой линии (это сторона прямоугольника, в середине которой расположены ворота) он должен нанести удар, если известно, что ширина этого футбольного поля равна 72 метрам, а ширина ворот равна 8 метрам? [5]. Эта задача предлагалась на олимпиаде «Ломоносов» в 2010 году.
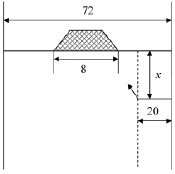
Рис. 1
Решение. Проведем через две штанги ворот (точки A и B на рис. 2) окружность, касающуюся прямой, по которой движется футболист (C – точка касания), то угол ACB – и есть искомый максимально возможный угол!
Покажем, что это действительно так. Действительно, угол ACB равен половине дуги AB, как вписанный. А угол с любой другой лежащей на этой прямой вершиной равен
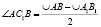
и будет меньше половины дуги АВ, то есть меньше угла АСВ.
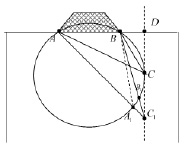
Рис. 2
Радиус этой окружности равен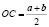 
(рис. 3). Поэтому по теореме Пифагора для треугольника ОВЕ имеем: 
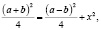где х – искомое расстояние. Значит, 
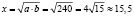(м).
Можно было бы здесь воспользоваться теоремой о касательной и секущей: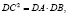 
то есть 
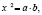откуда и следует ответ.
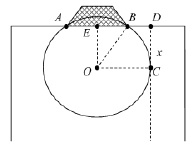
Рис. 3
Можно предложить учащимся решить эту задачу чисто аналитическими методами (с помощью теоремы косинусов и математического анализа; с помощью формулы тангенса разности двух углов и математического анализа; чисто алгебраическим методом).
Другой подход к решению этой задачи с использованием линий уровня читатель найдет в работе [4]. Приведенные в этой работе рассуждения покажут, что движение футболиста может осуществляться не обязательно по прямой, но и по любой траектории, а удар по футбольному мячу должен наноситься в момент касания этой траектории с окружностью, соответствующей максимальному углу.