При создании какого-либо программного обеспечения разработчик зачастую сталкивается с необходимостью вычисления кратного интеграла. Существует множество различных способов для их вычисления. Метод прямоугольников и метод Монте-карло являются наиболее используемыми. Чтобы узнать, какой из методов проявит себя более эффективным для решаемой задачи, была поставлена задача разработки программного средства сравнения методов вычисления кратных интегралов
2. Теоретические сведения
Метод правых прямоугольников представляет искомую площадь в виде суммы площадей малых прямоугольников. Составная квадратурная формула:
Простейшим вариант метода Монте-карло основан на геометрической вероятности.
Формула:
где SD - искомая площадь области D, SD* - площадь прямоугольной области D*, в которую заключена область D, m - количество точек, попавших внутрь области D, n - количество проведенных
Реализация метода монте-карло, основанного на интегральном среднем:
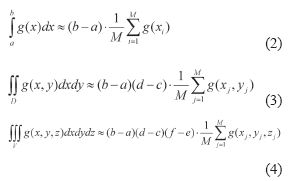
Приложение метода Vонте-карло, основанное на усреднении площадей:
3. Заключение по итогам разработки
В результате работы над данной темой в среде программирования Ms Visual Studio
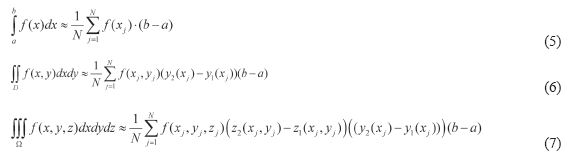
2008 на языке c# был создан программный продукт, отвечающий поставленным требованиям. Программа позволяет вычислять значения кратных интегралов для разных подынтегральных функций по различным областям интегрирования.
Для вычисления интеграла необходимо задать функцию, пределы интегрирования и параметры метода (количество экспериментов, либо величины шагов дискретизации).
После вычисления интеграла пользователь получает следующую выходную информацию: приближенное значение интеграла, абсолютная и относительная погрешности, время выполнения в мс.
Разработанный программный продукт позволяет провести ряд вычислительных экспериментов, на основе которых пользователь может построить статистику и сделать выводы об эффективности использования методов вычисления кратных интегралов для различных функций в различных областях интегрирования.
В дальнейшем планируется увеличение функционала программного средства посредством внедрения модуля трансляции математических выражений, модуля автоматического вычисления статистических параметров распределения наблюденных значений интегралов и их погрешностей, функций подсчета количества операций, производимых методом, и функций работы с приведенной погрешностью.
4. Результаты исследования
По результатам вычислительных экспериментов, проведенных для различных прямоугольных областей интегрирования, можно сделать следующие выводы.
1. Формула (1) является наиболее точной из выбранных методов. Уменьшение шагов дискретизации ведет не только к повышению точности вычислений, но и к значительному повышению временной сложности. Особенно сильно это отражается на двойных и тройных интегралах. С повышением кратности интеграла становится затруднительно использование этого метода, т.к., чтобы получить результат с небольшой погрешностью, необходимо уменьшать шаги дискретизации, что ведет к значительному росту временной сложности.
Также, на увеличение временной сложности влияет увеличение области интегрирования, т.к. увеличивается количество вычислений.
2. Формула (3) показала себя как самая быстрая, однако наблюдается достаточно большая и мало предсказуемая погрешность полученных значений для интегралов любой кратности.
3. Формула (3) и формула (4), показали одинаковые результаты, как и ожидалось, для прямоугольных областей интегрирования. Эти методы дают достаточно большую точность при небольшом времени выполнения для всех кратных интегралов.