Подготовка высококвалифицированного специалиста, в том числе и учителя, делает востребованными интерактивные технологии обучения, как наиболее результативные формы организации учебного процесса, при которых исключено безучастное присутствие обучаемого.
К таким интерактивным методам обучения относится кейс-метод (метод case-study). Этот метод представляется как наиболее эффективная современная образовательная технология в форме проблемно-ситуативного обучения, и относится к неигровым активным имитационным методам обучения.
Сущность кейс-метода заключается в активной самостоятельной деятельности обучающихся по разрешению противоречий в искусственно созданной профессиональной среде, которая позволяет группировать теоретические знания, практические навыки и накопленный жизненный опыт.
Результатом использования этого метода является творческое овладение обучающимися профессиональными знаниями, умениями и навыками и формирование ключевых компетенций по решению проблемы, развития аналитических умственных способностей.
Впервые кейс-метод был применен в учебном процессе в школе права Гарвардского университета в 1870 г.; внедрение этого метода в Гарвардской школе бизнеса началось в 1920 г., а первые подборки кейсов были опубликованы в 1925 г. в Отчетах Гарвардского университета о бизнесе [8].
А.М. Долгоруков [8] рассматривает метод case-study или метод конкретных ситуаций (от английского case – случай, ситуация) как метод активного проблемно-ситуационного анализа, основанный на обучении путем решения конкретных задач-ситуаций (решение кейсов). Сase-studies – учебные конкретные ситуации, специально разрабатываемые на основе фактического материала с целью последующего разбора на учебных занятиях.
Непосредственной целью метода-кейса является: совместными усилиями студентов группы проанализировать ситуацию – case, возникающую при конкретном положении дел, выработать практическое решение [3, 4, 8, 10].
Кейсы классифицируют по различным признакам. Приведем разновидности кейсов в зависимости от различных признаков: по сложности (иллюстративные учебные ситуации; учебные ситуации, в которых преследуется цель формулирования проблемы); исходя из цели и задач процесса обучения (кейсы, обучающие решению проблем и принятию решений; кейсы иллюстрирующие решение проблемы); по наличию сюжета (сюжетные, бессюжетные); по степени взаимодействия основных источников (практические, обучающие, научно-исследовательские) и др.
Выделяют различные виды анализа кейсов: проблемный анализ (предполагает осознание сущности, специфики той или иной проблемы и путей ее разрешения); причинно-следственный анализ (его основными понятиями выступают «причина» и «следствие»); прогматический анализ (предполагает осмысление того или иного объекта, процесса, явления с точки зрения более эффективного использования в практической жизни); аксиологический анализ (предполагает анализ того или иного объекта, процесса, явления в системе ценностей); ситуационный анализ (основывается на совокупности приемов и методов осмысления ситуации, ее структуры, определяющих ее факторов, тенденций развития и т.п.); прогностический анализ (предполагает не разработку, а использование моделей будущего и путей его достижения); рекомендательный анализ (ориентирован на выработку рекомендаций, относительно поведения действующих лиц в некоторых ситуациях); программно-целевой анализ (представляет собой дальнейшее развитие рекомендательного анализа в аспекте выработки программы достижения определенной цели).
Можно выделить следующие этапы в процессе решения кейсов:
– знакомство с ситуацией, ее особенностями;
– выделение основных проблем, факторов и субъектов, которые могут реально воздействовать на решение проблем;
– предложение различных аспектов проблемы для «мозгового штурма»;
– анализ последствий принятия того или иного решения;
– предложение одного или нескольких вариантов решения кейса.
Обсуждение кейсов может основываться на двух методах. Один из них носит название традиционного Гарвардского метода – открытая дискуссия. Другой метод связан с индивидуальным или групповым опросом.
Особое место в организации дискуссии при обсуждении и анализе кейса принадлежит использованию метода генерации идей, получившего название «мозговой атаки» или «мозгового штурма». Метод «мозгового штурма» выступает в качестве важнейшего средства развития творческой активности студентов в процессе обучения. Этот метод необходимо применять при возникновении у группы студентов реальных затруднений в осмыслении ситуации, как средство повышения активности обучающихся.
Кейс можно предложить студенту не только на занятиях, но и перед экзаменом, либо прямо на экзамене.
Источниками сюжетов для кейсов могут стать: проблемы общественной жизни; проблемы образования; проблемы науки.
Организация обсуждения кейса предполагает формулирование перед студентами вопросов, включения их в дискуссию (вопросы обычно следует предлагать студентам вместе с кейсом).
Как правило, во всех дискуссиях при обсуждении кейсов преподаватель должен сформулировать четыре вопроса: 1. Почему ситуация выглядит как дилемма?; 2. Кто принимал решение?; 3. Какие варианты решения имел тот, кто принимал решение?; 4. Что ему надо было сделать?
Важную роль играет представление результатов анализа кейса, которое вырабатывает навыки публичного общения, формирование у студентов своего собственного имиджа.
Завершая занятие, нельзя упускать из вида подведение итогов дискуссии. Преподаватель должен вновь взять контроль над ходом занятия в свои руки, обобщить проделанную работу, выделить в ней слабые и сильные стороны, назвав лучших и наиболее пассивных участников дискуссии, определить степень достижения поставленных учебных и воспитательных целей, указать конкретное задание для самостоятельной работы, объявить конечную оценку и ответить на возникшие в ходе занятия вопросы студентов.
Мы в своей работе метод-кейсов используем при обучении будущих учителей математики курсам «Современные тенденции в школьном математической образовании» (бакалавриат, магистратура), «Проблемы современной дидактики» (магистратура), «Типичные ошибки по математике, их причины и пути предупреждения» (магистратура).
Приведем примеры кейсов (по указанным выше источникам сюжета – это кейсы, исходящие из проблем обучения).
Кейс 1 [1]. В задании может содержаться математическая ошибка (как в условии задачи, так и в ответе и решении). Если некорректно условие задачи, то объясните, почему это так. Если неверно только решение, то укажите все ошибки и приведите верное решение.
Задача. Найдите два натуральных числа, сумма которых равна 119, а разность квадратов – простое число.
Решение
Пусть а и b − искомые числа, тогда a + b = 119 и число a2 – b2 − простое число. Так как a2 – b2 = (a + b)(a – b), то a – b = 1.
Решая систему уравнений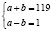 
, получим, что a =60, b = 59.
Ответ: a =60, b = 59.
Студенты должны прийти к выводу, что таких чисел нет. Если a – b = 1, то a2 – b2 = a + b = 119 = 7∙17, то есть 119 − составное число.
Это можно в равной степени трактовать либо как некорректность условия (сумма чисел должна быть простым числом), либо как ошибку в «решении» и «ответе» (после разложения на множители можно сразу делать вывод, что искомых чисел не существует).
Кейс 2. Приведено решение уравнения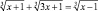 
.
Решение
Областью определения уравнения являются все действительные числа. Возведем обе части этого уравнения в куб. Будем иметь:
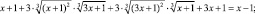
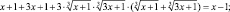
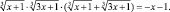
В последнее уравнение входит выражение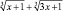 
, являющееся левой частью исходного уравнения. Заменим это выражение выражением, стоящим в правой части уравнения. Будем иметь 
.
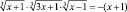Возведем обе части последнего уравнения в куб:
; 
,
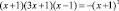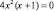откуда x1 = 0, x2 = – 1.
Обсуждая предложенное решение, студенты должны прийти к выводу о том, что x1 = 0 − посторонний корень и что он появился из-за замены выражения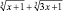 
ему нетождественно равным выражением 
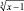. Об этом более подробно читатель сможет прочитать в нашей работе [5].
Кейс 3 [2]. В задании могут содержаться математические ошибки (как в условии задачи, так и в ответе и решении). Если некорректно условие задачи, то объясните почему это так. В этом случае проведите исследование данных в условии, показывающее, можно ли их изменить так, чтобы условие стало корректным. Если неверно только решение, то укажите все ошибки и приведите верное решение.
Задача. Один торговец продает сливы в среднем по 150 р. за килограмм, а другой − по 100 р. Но у первого косточка составляет треть массы каждой сливы, а у второго – половину. Чьи сливы выгоднее купить.
Решение
У первого торговца мякоть составляет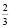 
массы, значит, 
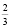килограмма мякоти у него стоит 100 р., а 1 кг мякоти – 150 р. У второго торговца мякоть составляет половину массы, поэтому ее стоимость – 50 р. за полкило, а 1 кг мякоти стоит 100 р. Таким образом, у второго покупать выгоднее.
В результате обсуждения кейса, студенты должны прийти к выводу о том, что условие задачи корректно, ответ верный, но в корне неверно решение.
Из верного утверждения «У первого торговца мякоть составляет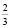 
массы» вовсе не следует, что 
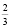килограмма мякоти у него стоит 100 р. На самом деле первый торговец берет 100 р. не за 
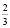килограмма мякоти слив, а за 
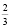килограмма слив вместе с косточками. А 150 р. он, как и сказано в условии задачи, берет за 1 кг слив, а не за 1 кг мякоти. Аналогично, второй торговец берет 150 р. за полкило слив (а не только мякоти), а 100 р. – за 1 кг слив. В решении путается мякоть слив и целые сливы, в результате чего приходят к абсурдному выводу: цена мякоти слив не отличается от указанной в условии цены слив с косточками (100 р.).
Приведем верное решение. Сравним цену мякоти слив. Первый торговец продает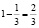 
килограммам мякоти за 150 р., то есть цена 1 кг мякоти у него составляет 
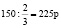. А у второго торговца мякоть стоит 100 р. за полкило, то есть 200 р. за килограмм. Таким образом, килограмм мякоти у второго торговца дешевле, поэтому покупать сливы выгоднее у него.
Может быть предложено и такое верное решение. За 300 р. у первого торговца будет куплено 2 кг слив, из которых мякоть составит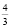 
кг, а у второго будет куплено 3 кг слив, причем мякоть составит 1,5 кг. Таким образом, покупать сливы у второго торговца выгоднее.
Кейс 4 [2]. Школьник решил задачу «Сколькими способами можно нарисовать прямоугольник по линиям сетки на клетчатом листе бумаги размером m∙n?», рассуждая следующим образом.
Каждый прямоугольник задается однозначно своей верхней левой и правой нижней вершинами. Выберем местоположение одной вершины, это можно сделать (m + 1)(n + 1) способами – таково число узлов решетки на листе размером m∙n. Второй узел не должен лежать с первым в одной строке и в одном столбце (а также не должен с ним совпадать). Таким образом, он может лежать в любой из n оставшихся строк и в любом из m оставшихся столбцов, то есть может быть выбран m∙n способами. Итого: по правилу произведения существует (m + 1)(n + 1)mn способов выбрать две вершины прямоугольника. Но при этом мы посчитали каждый прямоугольник два раза: выбирая сначала верхний левый, а затем нижний правый угол и наоборот, поэтому полученное произведение надо разделить на два.
Ответ: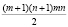 
.
В решении есть ошибки.
1. Придумайте аргумент, который сразу убедит школьника, что его решение неверное, не указывая, где именно он ошибся.
2. Укажите все ошибки в приведенном решении.
3. Приведите верное решение.
Ответы на вопросы могут быть такими.
1. На листе размером 1×1 − всего один прямоугольник, а по формуле, полученной школьником, их должно быть два.
2. В решении верно подсчитано количество способов выбрать две противоположные вершины прямоугольника. Но верхняя вершина может оказаться не левее, а правее нижней. В этом случае не существует прямоугольника, для которого одна из выбранных вершин – верхняя левая, а другая – правая нижняя.
Ответ: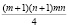 
.
Для получения этого верного ответа следует в приведенном школьником решении первое предложение заменить на другое: «Каждый прямоугольник однозначно задается двумя противоположными вершинами: либо верхней левой и нижней правой, либо верхней правой и нижней левой». Далее, как и в приведенном решении, получим, что существует (m + 1)(n + 1)mn способов выбрать две противоположные вершины прямоугольника. Но при этом каждый прямоугольник учтен четыре раза, так как любая из четырех вершин могла быть выбрана в качестве первой. Поэтому полученное произведение надо разделить на четыре.
Материал для таких кейсов можно найти в наших работах [6, 7].