Scientific journal

International Journal of Experimental Education

ISSN 2618–7159

ИФ РИНЦ = 0,425

Данная работа посвящена исследованию и анализу структуры медико-биологических показателей у детей с ожирением на основе статистических методов анализа данных. Это необходимо для того, чтобы выявить закономерности и взаимосвязи параметров до и после лечения.

Состояние здоровья детей является одной из наиболее значимых ценностей, от этого напрямую зависит благополучие всего общества в целом. При решении проблем связанных с ожирением детей требуется комплексный подход.

Интерес к проблеме ожирения не ослабевает так как, во-первых, ожирение, начавшееся именно в детском возрасте, с большей вероятностью приведет к раннему началу сосудистых заболеваний. Во-вторых, возрастает вероятность эндокринных осложнений. Таким образом, в настоящее время является актуальным изучение распространения ожирения и выявление его осложнений среди детского населения.

Объект исследования: дети с различными формами ожирения, у которых измерены различные медико-биологические показатели. Каждый объект описывается в виде вектора порядка n. Каждый элемент такого объекта – некоторая числовая характеристика. Так как, число данных велико и их анализ не представляется возможным без использования математического аппарата, то необходимо прибегнуть к статистическим методам.

В исследовании приняли участие 276 детей с ожирением, которые были распределены на 5 групп в зависимости от подхода к лечению. Возраст детей от 7 до 17 лет.

Предмет исследования: медико-биологические показатели у детей, страдающих ожирением. Для характеристики функционального состояния у детей определяли: объем талии, объем бедер, массу тела, индекс массы тела, диастолическое артериальное давление, индекс инсулинорезистентности, уровень холестерина и глюкозы.

Целью работы является определение взаимосвязи медико-биологических показателей у детей с ожирением, а также сравнение результатов до и после лечения.

Для достижения поставленной цели необходимо решить следующие задачи:

● проанализировать меры центральной тенденции и изменчивости;

● произвести сравнение выборок использованием t –критерия Cтьюдента, Манна-Уитни и критерия Уилкоксона;

● сравнить оценки показателей до и после лечения с помощью Н – критерия Уилкоксона;

Характеристика экспериментальных данных

В качестве исходной информации имеем сведения о детях с различными степенями ожирения, у которых измерены следующие показатели:

1. ОТ – Объем талии, см

Измеряют объем талии по самому узкому месту на животе. К сожалению, если избыток веса значительный – то измерить талию «на глаз» бывает тяжело, тогда измеряют объем талии посередине между краями реберной дуги и гребнями подвздошных костей (самая верхняя точка костей таза). Полученные размеры отмечают в конце нормального выдоха.

2. ОБ – Объем бедер, см

Объем бедер следует измерять в наиболее широком месте, вокруг бедер на уровне наиболее выступающей части ягодиц. Измерять объем бедер следует без одежды.

3. М – Масса тела, кг.

Масса тела в сочетании с другими антропометрическими признаками – важный показатель физического развития и состояния здоровья. Зависит от пола, роста, связана с характером питания, наследственностью, социально-экономическими условиями, а также с районом обитания. Обычно средняя масса тела мальчиков несколько больше средней массы тела девочек соответствующего возраста или равна ей, за исключением периода полового созревания девочек. Дневные колебания массы тела составляют ± 2 кг. Показатели массы тела часто используются для построения разного рода индексов и схем при диагностике физического развития.

4. ИМТ – Индекс массы тела

Индекс массы тела (англ. body mass index (BMI), ИМТ) – величина, позволяющая оценить степень соответствия массы человека и его роста и, тем самым, косвенно оценить, является ли масса недостаточной, нормальной или избыточной. Важен при определении показаний для необходимости лечения.

Индекс массы тела рассчитывается по формуле:

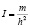, (1)

где m – масса тела в килограммах, h – рост в метрах, ИТМ измеряется в кг/м².

Показатель индекса массы тела разработан бельгийским социологом и статистиком Адольфом Кетеле (Adolphe Quetelet) в 1869 году. В соответствии с рекомендациями ВОЗ разработана следующая интерпретация показателей ИМТ:

Таблица 1

Показатели ИМТ

5. ДАД – диастолическое артериальное давление, мм.рт.ст

Нижнее число – диастолическое артериальное давление, показывает давление в артериях в момент расслабления сердечной мышцы. Это минимальное давление в артериях, оно отражает сопротивление периферических сосудов. По мере продвижения крови по сосудистому руслу амплитуда колебаний давления крови спадает, венозное и капиллярное давление мало зависят от фазы сердечного цикла.

6. HOMA – индекс инсулинорезистентности

О наличии инсулинорезистентности (ИР) можно косвенно судить по соотношению уровней глюкозы и инсулина натощак. Это соотношение учитывается в модели гомеостаза глюкозы (Homeostatic Model Assessment), и выражается индексом ИР (НОМАR ), который рассчитывают по формуле:

НОМАR = GoxINSo/22,5, (2)

где Go – концентрация глюкозы в плазме натощак (ммоль/л),

INSo – концентрация инсулина в сыворотке натощак (мкЕД/мл).

Индекс HOMAR считается информативным показателем в диагностике ИР, но его применение затруднено отсутствием норм для разных возрастных групп.

7. Холестерин – содержание холестерина в крови человека, ммоль/л

Холестерин – это липид (жир), который в основном образуется в печени и имеет ключевое значение для нормального функционирования организма.

Содержание холестерина в крови человека может варьировать от 3,6 ммоль/л до 7,8 ммоль/л. Рекомендуемый целевой уровень холестерина < 5 ммоль/л.

8. Глюкоза – уровень глюкозы в крови, ммоль/л

Глюкоза – основной показатель углеводного обмена. Более половины энергии, которую расходует наш организм, образуется за счет окисления глюкозы.

Концентрация глюкозы в крови регулируется гормонами: инсулин является основным гормоном поджелудочной железы. При его недостатке уровень глюкозы в крови повышается, клетки голодают.

Норма глюкозы у детей до 14 лет – 3,33–5,55 ммоль/л, у взрослых норма глюкозы в крови – 3,89–5,83 ммоль/л, с 60 лет уровень глюкозы в норме возрастает до 6,38 ммоль/л. Рост глюкозы происходит после сильных эмоций, стресса и курения, при неправильном питании.

9. Группа лечения, чел

Для каждой лечебной группы предназначен различный комплекс лечения. Первый комплекс – базовый, второй и третий – коррегированные, четвертый комплекс для больных с ожирением и метаболическим синдромом, а пятый дополненный для тех же больных (ожирение и метаболический синдром).

Математическая постановка задачи

Имеется выборка Xi, j из n объектов, характеризующихся m переменными. Где i − номер объекта, j − номер переменной (признака).

Задача заключается в анализе структуры экспериментальных многомерных медицинских данных на основе статистических методов.

Для решения поставленной задачи необходимо проанализировать существующие подходы к анализу данных такого типа, выбрать способ его компьютерной реализации.

Проведение исследований и анализ результатов

Меры центральной тенденции

Различные совокупности данных предполагают разные определения «центрального положения». Существуют три такие меры (мода, медиана и среднее). Более подробная информация о мерах центральной тенденции представлена в работе [6].

Наиболее просто получаемой мерой центральной тенденции является мода. Мода (чаще всего обозначается как М) – это такое значение в множестве наблюдений, которое встречается наиболее часто.

В совокупности значений (2, 6, 6, 8, 9, 9, 9, 10) модой является 9, потому что оно встречается чаще любого другого значения. Обратите внимание, что мода представляет собой наиболее частое значение (в данном примере 9), а не частоту появления этого значения (в примере равную 3).

Медиана (обозначается Мd) – это значение, которое делит упорядоченное множество данных пополам, так что одна половина значений оказывается больше медианы, а другая – меньше.

Если данные содержат нечетное число различных значений, например 11, 13, 18, 19, 20, то медиана есть центральное значение для случая, когда они упорядочены, т. е. Мd = 18.

Если данные содержат четное число различных значений, например 4, 9, 13, 14, то медиана есть точка, лежащая посредине между двумя центральными значениями, когда они упорядочены: Мd = (9 + 13)/2 = 11.

Теперь определим третью меру – выборочное среднее (называемое иногда «средним» или «арифметическим средним»).

Среднее совокупности n значений обозначается через x и определяется как

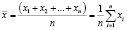. (3)

Каждая из приведенных выше мер центральной тенденции обладает характеристиками, которые делают ее ценной в определенных условиях. Мода наиболее просто вычисляется – ее можно определить на глаз. Кроме того, для очень больших групп данных это достаточно стабильная мера центра распределения. Во многих распределениях значительного числа измерений, используемых в педагогике и психологии, мода близка к двум другим мерам – медиане и среднему.

На величину среднего влияют значения всех результатов, особенно те результаты, которые можно назвать «выбросами», т. е. данные, находящиеся далеко от центра группы оценок. Медиана и мода не требуют для определения всех значений.

Меры изменчивости

К мерам изменчивости переменной относятся следующие характеристики: размах, дисперсия, среднее квадратическое (стандартное) отклонение и среднее линейное отклонение, коэффициент вариации.

Размах измеряет на числовой шкале расстояние, в пределах которого изменяются оценки. Поскольку существуют несколько иные определения размаха, то надо разграничить два его типа: включающий и исключающий.

Исключающий размах – это разность максимального и минимального значений в выборке [6]. Например, исключающий размах значений 0, 2, 3, 5, 8 равен 8 – 0 = 8. Значения: – 0,2; 0,4; 0,8; 1,6 имеют исключающий размах равный 1,6 – (– 0,2) = 1,8.

Включающий размах – это разность между естественной верхней границей интервала, содержащего максимальное значение, и естественной нижней границей интервала, включающего минимальное значение [6]. Или к величине исключающего размаха добавляют значение единицы точности измерения.

Например, рост пяти мальчиков измеряется с точностью до 1 сантиметра. Получены следующие значения:

Таким образом, включающий размах равен 168 – 149 = 18 + 1 = 19.

Размах представляет собой меру рассеяния, разброса, неоднородности или изменчивости. Эта величина возрастает с ростом рассеяния и уменьшением однородности. Размах является довольно грубой, но достаточно распространенной мерой изменчивости.

Более точной мерой изменчивости является дисперсия (обозначается D, 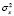или 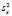, которая определяется по формуле

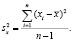(4)

Ценность дисперсии заключается в том, что, являясь мерой варьирования числовых значений признака вокруг его среднего значения, она измеряет внутреннюю изменчивость значений признака, зависящую от разностей между наблюдениями. Преимущество дисперсии перед другими показателями вариации состоит также и в том, что она разлагается на составные компоненты, позволяя тем самым оценивать влияние различных факторов на величину учитываемого признака.

Мерой изменчивости, тесно связанной с дисперсией, является стандартное отклонение. Среднее квадратическое или стандартное отклонение, обозначаемое σх или sх, определяется как положительное значение квадратного корня из дисперсии:

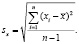(5)

Стандартное отклонение часто является полезной мерой вариации, так как для многих распределений мы приблизительно знаем, какой процент данных лежит внутри одного, двух, трех и более стандартных отклонений среднего. Например, мы можем знать, что 70 % значений лежит между 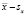и .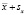

Еще одна мера изменчивости, среднее отклонение, используется реже. Отклонение каждого значения от среднего обозначается как 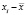. Совокупность всех n отклонений характеризует изменчивость в исходных данных. Однако сумма положительных и отрицательных отклонений вовсе не является мерой общей изменчивости в группе данных, ибо она всегда точно равна нулю. Если рассматривать отклонения как расстояние каждого объекта до 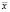без учета знака, то сумма этих расстояний будет характеризовать изменчивость данных, а именно

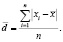(6)

Среднее отклонение не часто используется как мера изменчивости в связи с тем, что среднее отклонение не имеет теоретического обоснования в отличие, например, от дисперсии.

Любое множество n данных со средним 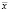и стандартным отклонением sх можно преобразовать в другое множество со средним 0 и стандартным отклонением 1 таким образом, что преобразованные значения будут непосредственно выражаться в отклонениях исходных значений от среднего, измеренных в единицах стандартного отклонения.

Новые значения называют значениями z:

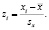(7)

Значение z – не только удобное средство информации о положении некоторого значения, связанного со средним и измеренного в единицах стандартного отклонения, но и шаг вперед к преобразованию множества Х в произвольную шкалу с удобными характеристиками среднего и стандартного отклонения. Сами оценки z могут не подходить для некоторых целей. Отрицательные оценки, например, могут оказаться неудобными, а множество z будет, конечно, содержать дроби. Преобразование самих z позволяет устранить эти несущественные трудности.

Известно, что значения cz, полученные умножением каждого z на константу с, будут иметь стандартное отклонение |с|, а для cz + d среднее равно d, а именно cz + d = с*0 + d = d.

В практике довольно часто приходится сравнивать изменчивость признаков, выраженных разными единицами. В таких случаях используют не абсолютные, а относительные показатели вариации. Дисперсия и среднее отклонение как величины, выражаемые теми же единицами, что и характеризуемый ими признак, для оценки изменчивости разноименных величин непригодны. Одним из относительных показателей вариации является коэффициент вариации. Этот показатель представляет собой среднее квадратическое отклонение, выраженное в процентах от величины среднего значения:

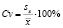. (8)

Различные признаки характеризуются различными коэффициентами вариации. Но в отношении одного и того же признака значение этого показателя Cv остается более или менее устойчивым и при симметричных распределениях обычно не превышает 50 %. Согласно [7] при сильно асимметричных рядах распределения коэффициент вариации может достигать 100 % и даже выше. Варьирование считается слабым, если не превосходит 10 %, средним, когда Cv составляет 11…25 %, и значительным при Cv > 25 %.

Рассчитанные меры центральной тенденции и изменчивости для всей выборки представлены в табл. 2. В табл. 3 и 4 представлены расчеты по всей выборке, разделенной на девочек и мальчиков.

Из данных, представленных в табл. 2–4, можно сделать следующие выводы.

Таблица 2

Меры центральной тенденции и изменчивости по всей выборке

Таблица 3

Меры центральной тенденции и изменчивости для девочек

Таблица 4

Меры центральной тенденции и изменчивости для мальчиков

Среди мальчиков наблюдается наиболее часто уменьшение объема талии на 2 см, в то время как среди девочек наиболее часто встречается уменьшение объема талии на 1 см. Тенденция к уменьшению объема бедер наблюдается как среди мальчиков, так и среди девочек, наиболее часто встречающееся значение уменьшение на 2 см. Также наблюдается уменьшение массы тела лечащихся, наиболее часто встречаемое значение на 2 кг, как среди мальчиков, так и среди девочек. Такие показатели как давление, НОМА, холестерин и глюкоза чаще всего остаются без изменения.

Наибольший вариационный размах имеет показатель давления, наименьший уровень глюкозы. Это можно объяснить тем, что мы исследуем данные, представленные в разных шкалах. Тем же самым можно объяснить большое значение среднеквадратического отклонения для показателя давления и маленькое для глюкозы.

Графическое представление полученных результатов, представлено на рис. 1–3. Из рисунков можно видеть, что по всей выборке показатели имеют тенденцию к уменьшению, такую же тенденцию имеют показатели по выборке среди мальчиков и среди девочек. По большому значению коэффициента вариации (больше 50 %) можно сделать заключение, что ряды не являются симметричными. Такой результат можно объяснить спецификой исследуемых данных.

В табл. 5 представлены рассчитанные меры центральной тенденции и изменчивости в зависимости от группы лечения.

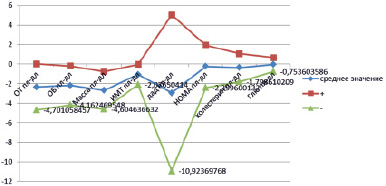
Рис. 1. Среднее значение и СКО по всей группе

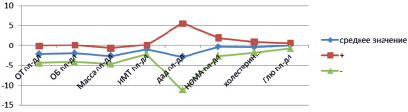
Рис. 2. Среднее значение и СКО по всей группе для девочек

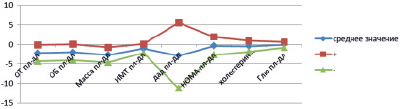
Рис. 3. Среднее значение и СКО по всей группе для мальчиков

Таблица 5

Меры центральной тенденции и изменчивости по группам лечения

Из данных, представленных в табл. 5, можно сделать следующие предположения.

Объем талии. Среди всех групп лечения наблюдается наиболее часто уменьшение объема талии, в частности, для групп 1, 3 и 5 наиболее часто встречается уменьшение на 1 см, для группы 4 на 2 см. В среднем, наибольшее уменьшение объема талии наблюдается в группе 3, наименьшее в группе 1.

Объем бедер. Тенденция к уменьшению объема бедер наблюдается во всех группах лечения, наиболее часто встречающееся значение уменьшение на 1 см в группах 3 и 5, на 2 см в группе 4 и в группе 1 наиболее часто значение объема бедер остаются без изменения. В среднем, наибольшее уменьшение объема бедер наблюдается в группе 5, наименьшее в группе 1.

Масса тела. Также наблюдается уменьшение массы тела лечащихся, наиболее часто встречаемое значение для группы 1 на 4 кг, для группы 2 на 2 кг, для группы 5 на 1,5 кг, для групп 3 и 4 наиболее часто значения массы тела остаются без изменения. В среднем, наибольшее уменьшение массы тела наблюдается в группе 1, наименьшее в группе 5.

Глюкоза. По этому показателю наблюдаются как положительные изменения, так и отрицательные. Для групп 3 и 5 наиболее часто встречается увеличение показателя уровня глюкозы на 0,2 ммоль/л, для группы 2 – уменьшение на 1,1 ммоль/л, для группы 4 наиболее часто значение уровня глюкозы остаются без изменения. В среднем, наибольшее уменьшение уровня глюкозы наблюдается в группе 5, наибольшее увеличение в группе 4.

Такие показатели как давление, НОМА и холестерин чаще всего остаются без изменения.

Наибольший вариационный размах имеет показатель давления, наименьший уровень глюкозы. Это можно объяснить тем, что мы исследуем данные, представленные в разных шкалах. Тем же самым можно объяснить большое значение среднеквадратического отклонения для показателя давления и маленькое для глюкозы.

Наибольшее значение коэффициента вариации наблюдается для показателя уровень холестерина для группы 3, наименьшее – индекс массы тела для группы 2.

Параметрический критерий проверки статистических гипотез t-критерий Стьюдента

Одним из наиболее распространенных параметрических критериев является критерий Стьюдента, в основе которого лежит t-распределение. Английский математик В. Госсет (печатавшийся под псевдонимом Стьюдент) в 1908 г. нашел закон распределения значений:

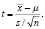(9)

Оказалось, что отношение разности между выборочной и генеральной средними к ошибке выборочной средней непрерывно распределяется согласно следующей формуле:

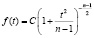для –∞ < t < +∞, (10)

где C – константа, зависящая только от степеней свободы v = n – 1.

Открытый Стьюдентом и теоретически обоснованный Р. Фишером закон t-распределения служит основой так называемой теории малой выборки, которая характеризует распределение выборочных средних в нормально распределяющейся совокупности в зависимости от объема выборки. Данное распределение зависит только от числа степеней свободы v = n – 1, причем с увеличением объема выборки n t-распределение быстро приближается к нормальному с параметрами m = 0 и s = 1 и уже при n > 30 не отличается от него.

Этот критерий применяют, когда некоторые показатели одного и того же объекта измеряются дважды: до и после эксперимента (например, лечения или обучения). Этот критерий подходит также для пар, в которых объекты подбираются по переменной, имеющей отношение к исследуемому измерению. Например, проверяя новый метод обучения иностранному языку, вы должны каждому студенту, обучающемуся новым способом, поставить в соответствие студента, занимающегося по традиционной программе.

В таких случаях средняя разность определяется по формуле

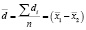, (11)

где di = x1i – x2i .

Н0-гипотеза сводится к предположению, что 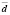= 0.

Ошибку средней разности 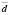, обозначаемую символом 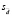, определяют по формулам:

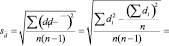
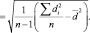(12)

Тогда t-критерий выразится в виде отношения средней разности к своей ошибке, т. е. 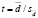. Если tэмп ≥ tкр (для принятого уровня значимости и числа степеней свободы v = n – 1), то нулевая гипотеза должна быть отвергнута.

Для вычисления эмпирического значения t-критерия в ситуации проверки гипотезы о различиях между двумя зависимыми выборками (например, двумя пробами одного и того же теста с временным интервалом) применяется следующая формула:

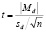(13)

где Md – средняя разность значений, sd – стандартное отклонение разностей, а n – количество наблюдений Эта статистика имеет распределение t(n – 1).

U-критерий Уилкоксона (Манна-Уитни)

Область применения U-критерия Уилкоксона – анализ двух независимых выборок. Размеры этих выборок могут различаться.

Назначение критерия – проверка гипотезы о статистической однородности двух выборок. Иногда эту гипотезу называют гипотезой об отсутствии эффекта обработки (имея в виду, что одна из выборок держит характеристики объектов, подвергшихся некоему воздействию, а другая – характеристики контрольных объектов). Он основан на попарном сравнении результатов из первой и второй выборок.

Ограничения критерия

1. В каждой выборке должно быть не менее 3 наблюдений: т и n ≥ 3 допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.

2. В каждой выборке должно быть не более 60 наблюдений; т и n ≤ 60. Однако уже при т, n > 20 ранжирование становиться достаточно трудоемким.

Порядок расчета

1. Расположить числовые значения сравниваемых выборок в возрастающем порядке в один общий ряд и пронумеровать члены общего ряда от 1 до N = m + n. Эти номера будут «рангами» членов ряда. Одинаковым значениям присваивается средний ранг.

2. Отдельно для каждой выборки найти суммы рангов R и определить величины:

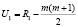и

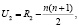
которые отображают связь между суммами рангов первой и второй выборки.

3. В качестве U-критерия использовать меньшую величину Uэмп, которую нужно сравнить с табличным значением Uкр . Условием для сохранения принятой Н0-гипотезы служит неравенство Uэмп > Uкр . Критические точки U-критерия Uкр для m и n и принимаемого уровня значимости a содержатся в статистических таблицах.

Результаты проведения анализа в пакете STATGRAPHICS по t-критерию Стьюдента и U-критерию Уилкоксона представлены в табл. 6 и 7.

В результате анализа полученных результатов из табл. 6 и 7 можно увидеть: t-критерий Стьюдента выявил один достоверный показатель, U-критерий Уилкоксона (Манна-Уитни) – три достоверных показателя. Различие в полученных результатах можно объяснить малым объемом выборки. Следовательно в данной ситуации лучше использовать критерий Манна-Уитни.

Таблица 6

t-критерий Стьюдента

Таблица 7

U-критерий Уилкоксона(Манна-Уитни)

Оба критерия выявляют достоверное различие оценок по такому показателю, как индекс массы тела. U-критерий Уилкоксона (Манна-Уитни) также определил достоверное различие по показателям холестерин и масса. Следовательно, по результатам экспертных оценок можно сделать предположение, что дети из первой группы лечения имеют лучшую динамику изменения индекса массы тела, чем дети из группы 5 и примерно одинаковые свойства и уровни в остальных случаях по обеим критериям. Для критерия Манна-Уитни можно предположить, что дети из первой группы лечения имеют лучшую динамику изменения индекса массы тела, массы и уровня холестерина, чем дети из группы 5 и примерно одинаковые свойства и уровни в остальных случаях.

Н-критерий Крускала–Уоллиса

Критерий предназначен для оценки различий одновременно между тремя, четырьмя и так далее выборками по уровню какого-либо признака.

Он позволяет установить, что уровень признака изменяется при переходе от группы к группе, но не указывает на направление этих изменений.

Гипотезы для критерия Крускала–Уоллиса формулируются следующим образом:

Н0: Между выборками 1, 2, 3 и так далее существуют лишь случайные различия по уровню исследуемого признака.

Н1: Между выборками 1, 2, 3 и так далее существую неслучайные различия по уровню исследуемого признака.

Н-критерий иногда рассматривается как непараметрический аналог метода дисперсионного однофакторного анализа для несвязных выборок [3].

Данный критерий является продолжением критерия U на большее, чем две сопоставляемые выборки. Все индивидуальные значения ранжируются так, как если бы это была одна большая выборка. Затем все индивидуальные значения возвращаются в свои первоначальные выборки, и мы подсчитываем суммы полученных ими рангов отдельно по каждой выборке. Если различия между выборками случайны, суммы рангов не будут различаться сколько-нибудь существенно, так как высокие и низкие ранги равномерно распределятся между выборками. Но если в одной из выборок будут преобладать низкие значения рангов, в другой – высокие, а в третьей – средние, то критерий Н позволит установить эти различия.

Теперь познакомимся с алгоритмом подсчета Н-критерия Крускала–Уоллиса.

1. Необходимо составить общий упорядоченный ряд. Результаты эксперимента расположены в порядке их возрастания.

2. Проранжировать значения, приписывая меньшему значению меньший ранг. Общее количество рангов равно количеству испытуемых в выборке.

3. Подсчитать сумму рангов отдельно по каждой группе. Проверить совпадение общей суммы рангов с расчетной.

4. Подсчитать значение Н-критерия по формуле

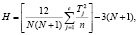(14)

где N – общее количество испытуемых в объединенной выборке; с – количество групп (выборок); n – количество испытуемых в каждой группе; Тj – суммы рангов по каждой группе.

5. При количестве групп с = 3 и n1, n2, n3 ≤ 5 определить критическое значение и соответствующий им уровень значимости (см. [6]). Если Hэмп равна или превышает критическое значение при уровне значимости p = 0,05 (обозначается Н0,05), Н0 отвергается.

При количестве групп с > 3 или количестве испытуемых n1, n2, n3 > 5 критические значения определятся как критические значения χ2 ([6]).

Если Hэмп равен или превышает критическое значение χ2, Н0 отвергается.

Ограничения критерия.

1. При сопоставлении трех выборок допускается, чтобы в одной из них n = 3, а в других n = 2. Но при таких численных составах выборок мы сможем установить различия на низшем уровне значимости (р ≤ 0,05).

Для того чтобы оказалось возможным диагностировать различия на более высоком уровне значимости (р ≤ 0,01), необходимо, чтобы в каждой выборке было не менее 3 наблюдений, или чтобы по крайней мере в одной из них было 4 наблюдения, а в других – по 2; при этом неважно, в какой именно выборке сколько испытуемых, а важно соотношение 4:2:2.

2. При большом количестве выборок и испытуемых в каждой выборке необходимо пользоваться таблицей критических значений критерия χ2, поскольку критерий Крускала–Уоллиса асимптотически приближается к распределению χ2 [3].

Количество степеней свободы при этом определяется по формуле v = c –1, где с – количество выборок.

Результаты проведения анализа в пакете STATGRAPHICS по H-критерию Крускала–Уоллиса представлены в табл. 8 и 9.

В табл. 8 представлена оценка достоверности различий. Из табл. 8 видно, что все различия для данных групп показателей являются достоверными. В табл. 9 представлены значения различий между группами.

Таблица 8

Оценка достоверности различий

Из табл. 9 видно, что самое маленькое различие наблюдается среди группы 1–3 по показателю уровень холестерина. Самое большое различие наблюдается среди групп 4–5 по показателю уровень глюкозы. Наименьшее различие по показателям 4–5, 2–4 и 2–3.

Сравнение оценок показателей у больных ожирением детей до и после лечения с использованием T -критерия Уилкоксона

Т-Критерий Уилкоксона – непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных измерений. Впервые предложен Фрэнком Уилкоксоном.

Критерий предназначен для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность, то есть, способен определить, является ли сдвиг показателей в одном направлении более интенсивным, чем в другом.

Критерий применим в тех случаях, когда признаки измерены, по крайней мере, в порядковой шкале. Целесообразно применять данный критерий, когда величина самих сдвигов варьирует в некотором диапазоне (10–15 % от их величины). Это объясняется тем, что разброс значений сдвигов должен быть таким, чтобы появлялась возможность их ранжирования. В случае если сдвиги незначительно отличаются между собой, и принимают какие-то конечные значения, например. + 1, – 1 и 0, формальных препятствий к применению критерия нет, но, ввиду большого числа одинаковых рангов, ранжирование утрачивает смысл, и те же результаты проще было бы получить с помощью критерия знаков [4, 7].

Суть метода состоит в том, что мы сопоставляем абсолютные величины выраженности сдвигов в том или ином направлении. Для этого сначала все абсолютные величины сдвигов ранжируются, а потом суммируются ранги. Если сдвиги в ту или иную сторону происходят случайно, то и суммы их рангов окажутся примерно равны. Если же интенсивность сдвигов в одну сторону больше, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.

Результаты проведения анализа в пакете STATGRAPHICS по Т-критерию Уилкоксона и знаковому тесту представлены в табл. 10 и 15.

Следует отметить, что критерий Уилкоксона выявляет только наличие различия между выборками, но не указывает, как именно они различаются.

Таблица 9

Различия показателей между группами лечения

Таблица 10

Сравнение оценок показателей до и после лечения с использованием критерия Т-критерия Уилкоксона по всей выборке

Таблица 11

Сравнение оценок показателей до и после лечения с использованием критерия Т-критерия Уилкоксона по группе 1

Таблица 12

Сравнение оценок показателей до и после лечения с использованием критерия Т-критерия Уилкоксона по группе 2

Таблица 13

Сравнение оценок показателей до и после лечения с использованием критерия Т-критерия Уилкоксона по группе 3

Таблица 14

Сравнение оценок показателей до и после лечения с использованием критерия Т-критерия Уилкоксона по группе 4

Таблица 15

Сравнение оценок показателей до и после лечения с использованием критерия Т-критерия Уилкоксона по группе 5

По табл. 10 можно сделать вывод, что лечение оказало наибольшее влияние на изменение показателей давления, холестерина, массы тела, индекса массы тела, объема талии и объема бедер, а влияния на другие параметры влияния не выявлено, так как различия не достоверны. По результатам можно предполагать, что лечение в общем оказывает существенное влияние на данные показатели детей с ожирением (выявлено шесть достоверных различий).

Такие же данные для детей с первой группой лечения.

Для детей из второй лечебной группы лечение оказало наибольшее влияние на изменение показателей давления, массы тела и индекса массы тела, а влияния на другие параметры влияния не выявлено, так как различия не достоверны. По результатам можно предполагать, что лечение оказывает не существенное влияние на данные показатели детей с ожирением (выявлено всего три достоверных различия).

Для детей из третьей лечебной группы лечение оказало наибольшее влияние на изменение показателей давления, массы тела, индекса массы тела, объема талии и объема бедер, а влияния на другие параметры влияния не выявлено, так как различия не достоверны. По результатам можно предполагать, что лечение оказывает существенное влияние на данные показатели детей с ожирением (выявлено пять достоверных различий).

Для детей из четвертой и пятой лечебных групп лечение оказало наибольшее влияние на изменение показателей массы тела, индекса массы тела, объема талии и объема бедер, а влияния на другие параметры влияния не выявлено, так как различия не достоверны. По результатам можно предполагать, что лечение оказывает влияние на данные показатели детей с ожирением, но не существенное (выявлено четыре достоверных различия).

В результаре анализа можно сделать вывод, что лучшие показатели сдвигов наблюдаются у детей первой лечебной группы. Не на много отличаются показатели у детей третьей группы лечения. Самые худшие результаты у детей из второй группы лечения.

Из полученных результатов можно сделать предположение: детям из третьей группы лечения назначить другой вид лечения.

Заключение. В результате исследования были самостоятельно изучены меры центральной тенденции (мода, медиана, среднее значение) и изменчивости (среднеквадратическое отклонение, вариационный размах, коэффициент вариации), t –критерий Cтьюдента, критерий Манна-Уитни и критерия Уилкоксона. С использованием данных методов решена прикладная задача исследования эффективности лечения детей, страдающих ожирением.

Исследованы медико-биологические показатели у детей с ожирением и выявлены закономерности и взаимосвязи параметров до и после лечения, а именно:

● проанализированы меры центральной тенденции и изменчивости;

● произведено сравнение выборок использованием t –критерия Cтьюдента, Манна-Уитни и критерия Уилкоксона;

● произведено сравнение оценок показателей до и после лечения с помощью Н – критерия Уилкоксона;

Статистический анализ показателей проводился в прикладном пакете программ Statagraphics.

При проведении анализа мер тенденции и изменчивости получили, что значение показателей имеет положительную тенденцию к уменьшению, как среди мальчиков, так и среди девочек.

В результате сравнения двух выборок с помощью t-критерия Стьюдента и критерия Манна-Уитни лучший результат показал второй критерий. t-критерий Стьюдента выявил один достоверный показатель, U-критерий Уилкоксона – три достоверных показателя. Оба критерия выявили достоверное различие оценок по показателю – индекс массы тела.

По критерию Уилкоксона выявлено, что лечение, в общем, по группе оказывает влияние на больных. Наибольшее влияние оказывает лечение на детей из первой группы лечения, наименьшее – на детей из второй группы.