Кейс-метод (метод case-study) относится к интерактивным методам обучения. Этот метод представляется как наиболее эффективная современная образовательная технология в форме проблемно-ситуативного обучения, и относится к неигровым активным имитационным методам обучения.
Сущность кейс-метода заключается в активной самостоятельной деятельности обучающихся по разрешению противоречий в искусственно созданной профессиональной среде, которая позволяет группировать теоретические знания, практические навыки и накопленный жизненный опыт.
Непосредственной целью метода-кейса является: совместными усилиями студентов группы проанализировать ситуацию – case, возникающую при конкретном положении дел, выработать практическое решение [1, 2, 6, 8].
Кейсы классифицируют по различным признакам. Приведем разновидности кейсов в зависимости от различных признаков: по сложности (иллюстративные учебные ситуации; учебные ситуации, в которых преследуется цель формулирования проблемы); исходя из цели и задач процесса обучения (кейсы, обучающие решению проблем и принятию решений; кейсы иллюстрирующие решение проблемы); по наличию сюжета (сюжетные, бессюжетные); по степени взаимодействия основных источников (практические, обучающие, научно-исследовательские) и др.
Выделяют различные виды анализа кейсов: проблемный анализ (предполагает осознание сущности, специфики той или иной проблемы и путей ее разрешения); причинно-следственный анализ (его основными понятиями выступают «причина» и «следствие»); прогматический анализ (предполагает осмысление того или иного объекта, процесса, явления с точки зрения более эффективного использования в практической жизни); аксиологический анализ (предполагает анализ того или иного объекта, процесса, явления в системе ценностей); ситуационный анализ (основывается на совокупности приемов и методов осмысления ситуации, ее структуры, определяющих ее факторов, тенденций развития и т.п.); прогностический анализ (предполагает не разработку, а использование моделей будущего и путей его достижения); рекомендательный анализ (ориентирован на выработку рекомендаций, относительно поведения действующих лиц в некоторых ситуациях); программно-целевой анализ (представляет собой дальнейшее развитие рекомендательного анализа в аспекте выработки программы достижения определенной цели).
Обсуждение кейсов может основываться на двух методах. Один из них носит название традиционного Гарвардского метода – открытая дискуссия. Другой метод связан с индивидуальным или групповым опросом [6].
Особое место в организации дискуссии при обсуждении и анализе кейса принадлежит использованию метода генерации идей, получившего название «мозговой атаки» или «мозгового штурма». Метод «мозгового штурма» выступает в качестве важнейшего средства развития творческой активности студентов в процессе обучения. Этот метод необходимо применять при возникновении у группы студентов реальных затруднений в осмыслении ситуации, как средство повышения активности обучающихся.
Кейс можно предложить студенту не только на занятиях, но и перед экзаменом, либо прямо на экзамене.
Источниками сюжетов для кейсов могут стать: проблемы общественной жизни; проблемы образования; проблемы науки.
Организация обсуждения кейса предполагает формулирование перед студентами вопросов, включения их в дискуссию (вопросы обычно следует предлагать студентам вместе с кейсом).
Важную роль играет представление результатов анализа кейса, которое вырабатывает навыки публичного общения, формирование у студентов своего собственного имиджа.
Завершая занятие, нельзя упускать из вида подведение итогов дискуссии. Преподаватель должен вновь взять контроль над ходом занятия в свои руки, обобщить проделанную работу, выделить в ней слабые и сильные стороны, назвав лучших и наиболее пассивных участников дискуссии, определить степень достижения поставленных учебных и воспитательных целей, указать конкретное задание для самостоятельной работы, объявить конечную оценку и ответить на возникшие в ходе занятия вопросы студентов.
Мы в данной статье рассмотрим использование метода кейсов в обучении будущих учителей математики курсу «Типичные ошибки по математике, их причины и пути предупреждения» (магистратура).
Приведем примеры кейсов (по указанным выше источникам сюжета – это кейсы, исходящие из проблем обучения).
Кейс 1. В задании может содержаться математическая ошибка (как в условии задачи, так и в ответе и решении). Если некорректно условие задачи, то объясните, почему это так. Если неверно только решение, то укажите все ошибки и приведите верное решение.
Задача. Найдите два натуральных числа, сумма которых равна 119, а разность квадратов – простое число.
Решение
Пусть a и b − искомые числа, тогда 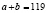 и число
и число 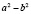 − простое число. Так как
− простое число. Так как 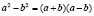 , то
, то 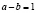 .
.
Решая систему уравнений
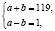
получим, что 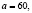
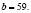
Ответ: 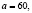
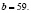
Студенты должны прийти к выводу, что таких чисел нет. Если 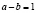 , то
, то 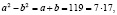 то есть 119 − составное число.
то есть 119 − составное число.
Это можно в равной степени трактовать либо как некорректность условия (сумма чисел должна быть простым числом), либо как ошибку в «решении» и «ответе» (после разложения на множители можно сразу делать вывод, что искомых чисел не существует).
Кейс 2. Приведено решение уравнения
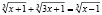 .
.
Решение
Областью определения уравнения являются все действительные числа. Возведем обе части этого уравнения в куб. Будем иметь:
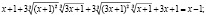
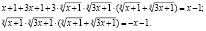
В последнее уравнение входит выражение 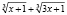 , являющееся левой частью исходного уравнения. Заменим это выражение выражением, стоящим в правой части уравнения. Будем иметь
, являющееся левой частью исходного уравнения. Заменим это выражение выражением, стоящим в правой части уравнения. Будем иметь 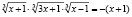 .
.
Возведем обе части последнего уравнения в куб:
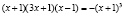 ;
; 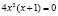 ,
,
откуда 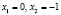 .
.
Обсуждая предложенное решение, студенты должны прийти к выводу о том, что 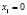 − посторонний корень и что он появился из-за замены выражения
− посторонний корень и что он появился из-за замены выражения 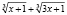 ему нетождественно равным выражением
ему нетождественно равным выражением 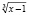 . об этом более подробно читатель сможет прочитать в нашей работе [3].
. об этом более подробно читатель сможет прочитать в нашей работе [3].
Кейс 3. Задачу «Вычислить значение выражения 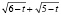 , если известно, что
, если известно, что 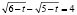 студент решил следующим образом.
студент решил следующим образом.
Решение
Положим, что 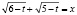 . Умножим почленно это равенство на равенство
. Умножим почленно это равенство на равенство 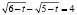 , будем иметь:
, будем иметь: 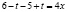 , откуда следует
, откуда следует 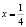 .
.
В задании может содержаться математическая ошибка (как в условии задачи, так и в ответе и решении). Если некорректно условие задачи, то объясните, почему это так. Если неверно только решение, то укажите все ошибки и приведите верное решение.
В результате обсуждения студенты должны прийти к выводу, что задание сформулировано некорректно. Действительно. Найдем непосредственно t из заданного в условии задачи равенства
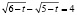 ;
;
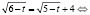
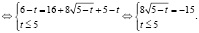
Видно, что в левой части уравнения стоит арифметический квадратный корень, а по определению он неотрицательный. Так как правая часть уравнения отрицательна, а ее левая часть неотрицательна, то уравнение корней не имеет, а это значит, что невозможно и найти значение выражения 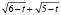 .
.
Кейс 4. Предложено пять способов решения одного и того же тригонометрического уравнения 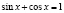 . Студенту предлагается указать какие решения ошибочны и в каких записанных ответах содержатся ошибки.
. Студенту предлагается указать какие решения ошибочны и в каких записанных ответах содержатся ошибки.
Способ 1. Возведем обе части уравнения в квадрат. Будем иметь:
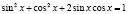 ;
;
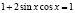 ;
; 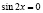 ;
; 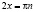 ,
,
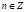 ;
; 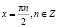 .
.
Ответ: 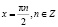 .
.
В результате анализа предложенного решения, студент должен прийти к выводу, что получены посторонние корни, так как при возведении в квадрат вместо равносильного уравнения получается уравнение следствие.
Способ 2. Воспользуемся формулами синуса и косинуса двойного угла и основным тригонометрическим тождеством. Будем иметь
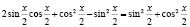 ;
;
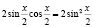 .
.
Разделим обе части последнего уравнения на 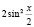 . Будем иметь:
. Будем иметь:
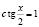 ;
; 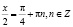 .
.
Ответ: 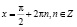 .
.
Обсуждая ситуацию, студенты должны прийти к выводу о том, что потеряна часть корней при решении однородного уравнения: значения переменной, для которых 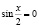 , также являются корнями исходного уравнения.
, также являются корнями исходного уравнения.
Способ 3. Используя формулу тангенса половинного угла, будем иметь:
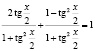 ;
;
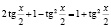
то есть
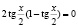 ;
; 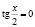 или
или 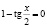 ,
,
откуда
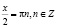 или
или 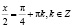 .
.
Ответ: 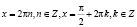 .
.
Анализ, проведенный студентами, должен показать им, что ответ верный и что прежде чем использовать формулы, выражающие синус и косинус через тангенс половинного угла, необходимо проверить, что значения x, при которых 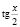 не определен, не являются решениями исходного уравнения. Для
не определен, не являются решениями исходного уравнения. Для 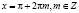 − это действительно выполняется, поэтому указанная ошибка не повлияла на ответ.
− это действительно выполняется, поэтому указанная ошибка не повлияла на ответ.
Способ 4. Умножив обе части уравнения на 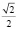 , студенты будут иметь:
, студенты будут иметь:
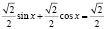 ;
;
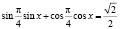 ,
,
откуда
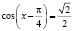 ,
, 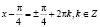 ;
;
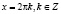 и
и 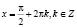 .
.
Ответ: 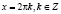 и
и 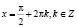 .
.
В результате анализа ситуации студенты должны осознать, что неграмотно записан ответ: союз «и» здесь неуместен, так как означает пересечение множеств, а должно быть объединение.
Способ 5. Используя основное тригонометрическое тождество, студенты записывают исходное уравнение в виде
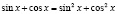 ;
;
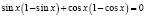 .
.
Используя условие, которое вытекает из исходного уравнения (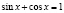 ), будем иметь
), будем иметь 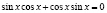 , откуда
, откуда
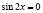 ;
; 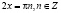 ;
; 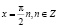 .
.
Ответ: 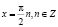 .
.
Анализ приведенного решения должен привести студентов к выводу о том, что получены посторонние корни, так как выполненная замена также привела к уравнению следствию.
Материал для таких кейсов можно найти в наших работах [4, 5].

