Постановка задачи при нестационарных волновых воздействиях
В настоящее время оценка точности и достоверности моделирования быстропротекающих процессов в областях различной формы является приоритетной задачей фундаментальной и прикладной науки. Некоторая информация о постановке и численной реализации нестационарных волновых задач механики деформируемого твердого тела приведена в следующих работах [1–10]. для решения задачи о моделировании упругих волн в деформируемых областях сложной формы рассмотрим некоторое тело Г в прямоугольной декартовой системе координат XOY, которому в начальный момент времени t=0 сообщается механическое воздействие. Предположим, что тело Г изготовлено из однородного изотропного материала, подчиняющегося упругому закону Гука при малых упругих деформациях.
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид
, 
, 
,
, 
, 
, 
, 
, 
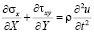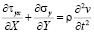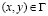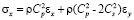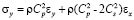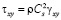
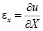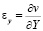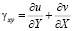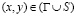, (1)
где 
, 
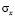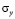и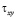 
– компоненты тензора упругих напряжени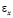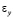й; 
, 
и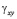 
– компоненты тензора упругих деформаци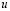й; 
и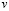 
– составляющие вектора упругих перемещений вдоль осе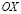й 
и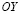 
соответственно; 
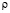– плотность материала; 
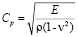– скорость продольной упругой волны; 
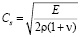– скорость поперечной упругой волны; n – коэффициент Пуассона; Е – модуль упругости; 
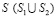– граничный контур тела Г.
Систему (1) в области, занимаемой телом Г, следует интегрировать при начальных и граничных условиях.
Разработка методики и алгоритма
Для решения двумерной нестационарной динамической задачи математической теории упругости с начальными и граничными условиями (1) используем метод конечных элементов в перемещениях.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела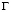 
, записываем приближенное значение уравнения движения в теории упругости
, 
,
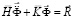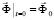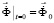, (2)
где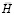 
– диагональная матрица инерции; 
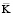– матрица жесткости; 
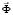– вектор узловых упругих перемещений; 
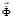– вектор узловых упругих скоростей перемещений; 
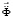– вектор узловых упругих ускорений; 
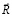– вектор внешних узловых упругих сил.
Интегрируя уравнение (2) конечноэлементным вариантом метода Галеркина, получим явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
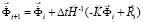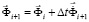. (3)
Шаг по временной переменной координате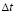 
выбирается из следующего соотношения
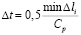
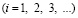, (4)
где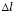 
– длина стороны конечного элемента.
На основе метода конечных элементов в перемещениях разработана методика, разработан алгоритм и составлен комплекс программ для решения двумерных линейных и нелинейных задач при различных начальных и граничных условиях, для областей сложной формы. Комплексы программ написаны на алгоритмическом языке Фортран-90.
Предложен квазирегулярный подход к решению систем линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями и к аппроксимации исследуемой области. Методика основывается на схемах: точка; линия; плоскость.
В работах [1–6, 8–9] приведена информация о физической достоверности и математической точности применяемого численного метода, алгоритма и комплекса программ при решении задач моделирования нестационарных волн напряжений в деформируемых телах различной формы.
Моделирование распространения плоских продольных упругих волн в полуплоскости
Рассмотрим задачу о воздействии плоской продольной волны в виде импульсного воздействия (первая ветвь: восходящая часть – четверть круга, нисходящая часть – четверть круга; вторая ветвь: восходящая часть – линейная, нисходящая часть – линейная) (рис. 2) на упругую полуплоскость (рис. 1).
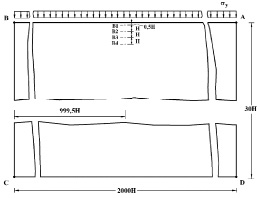
Рис. 1. Постановка задачи о распространении плоских продольных волн в упругой полуплоскости
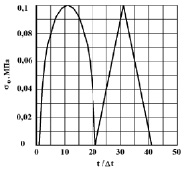
Рис. 2. Импульсное воздействие (первая ветвь: восходящая часть – четверть круга, нисходящая часть – четверть круга; вторая ветвь: восходящая часть – линейная, нисходящая часть – линейная)
На границе полуплоскости AB приложено нормальное напряжение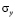 
, которое при 
(
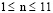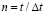) изменяется от 0 до P, при 
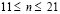изменяется от 
до 
, при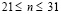 
изменяется от 0 до P и при 
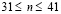изменяется от P до 0 (
, 
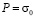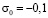МПа). Граничные условия для контура BCDA при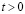 
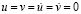. Отраженные волны от контура BCDA не доходят до исследуемых точек при 
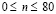. Расчеты проведены при следующих исходных данных: 
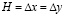; ∆t = 9,263⋅10-7 с; E = 7,1⋅104 МПа; n= 0,34; r= 2,755⋅103 кг/м3; Cp= 5398 м/с; Cs= 3078 м/с. Исследуемая расчетная область имеет 62031 узловую точку. Решается система уравнений из 248124 неизвестных.
В данном случае можно использовать условия на фронте плоской волны. Предположим, что от некоторых точек упругой среды производится какое-то возмущение. Тогда из этих точек во все стороны начинают излучаться волны. на некотором расстоянии от центра возмущения рассматриваемые волны можно представить как плоские. Тогда все частицы движутся параллельно направлению распространения волны. Такие волны принято считать плоскими.
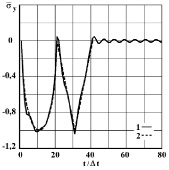
Рис. 3. Изменение нормального напряжения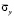 
во времени 
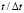в точке B1: 1 – численное решение; 2 – аналитическое решение
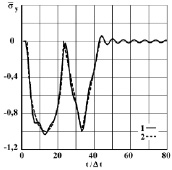
Рис. 4. Изменение нормального напряжения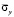 
во времени 
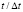в точке B2: 1 – численное решение; 2 – аналитическое решение
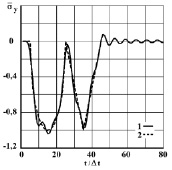
Рис. 5. Изменение нормального напряжения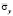 
во времени 
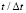в точке B3: 1 – численное решение; 2 – аналитическое решение
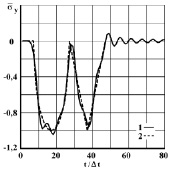
Рис. 6. Изменение нормального напряжения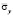 
во времени 
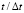в точке B4: 1 – численное решение; 2 – аналитическое решение
На фронте плоской продольной волны имеются следующие аналитические зависимости для плоского напряженного состояния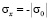 
и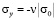 
. Отсюда видим, что точное решение задачи соответствует воздействию 
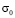(рис. 2). На рис. 3–6 показано изменение нормального напряжения 
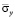во времени 
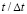в точках B1–B4: 1 – численное решение; 2 – аналитическое решение.
Для упругих нормальных напряжени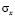й 
и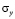 
имеется хорошее качественное и количественное согласование с результатами точного решения.
На основании проведенных исследований можно сделать вывод о физической достоверности и математической точности результатов численного решения задач о распространении нестационарных упругих волн в деформируемых телах.
Выводы
На основе метода конечных элементов в перемещениях разработаны методика, алгоритм и комплекс программ для решения линейных двумерных плоских задач, которые позволяют решать сложные задачи при воздействии нестационарных волн напряжений на различные объекты. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Задачи решаются методом сквозного счета, без выделения разрывов.
Решена задача о распространении плоских продольных волн в виде импульсного воздействия в упругой полуплоскости. Исследуемая расчетная область имеет 62031 узловую точку. Решается система уравнений из 248124 неизвестных. для решения поставленной задачи используется импульсное воздействие (первая ветвь: восходящая часть – четверть круга, нисходящая часть – четверть круга; вторая ветвь: восходящая часть – линейная, нисходящая часть – линейная).
Проведенные исследования позволяют сделать вывод о физической достоверности и математической точности результатов численного решения полученных, с помощью метода конечных элементов в перемещениях, при решении задач о распространении нестационарных упругих волн напряжений в деформируемых телах.