Поскольку жесткие условия химических заводов не гарантируют безаварийную эксплуатацию производств, то представляют интерес химические методы борьбы с ядовитыми газовыми образованиями, способные существенно снизить в них концентрацию H2S и PH3. Причем такой обычный прием, как сжигание в данном случае проблему не решает, так как в результате сгорания H2S и PH3 образуется примерно тоже количество сернистого ангидрида – SO2, отравляющее воздействие которого не многим уступает сероводороду. С теоретической точки зрения проблема может быть решена путем распыления в ядовитом облаке специальных веществ, вступающих с H2S и PH3 в химическую реакцию, приводящую к выпадению сульфитов не дающую побочного отравляющего эффекта. Для подтверждения формулированной теоретической посылки и точного определения состава нейтрализующих веществ требуются экспериментальные научно-исследовательские работы, в которых эффективность предложенного метода и его конкретные параметры были бы проверены в условиях, близких к реальным.
Экспериментально оптическим методом были определены состав смеси газов и аэразоли на определенной высоте при помощи лазерного дистанционного контроля и сняты ИК–спектры молекулы H2S и PH3.
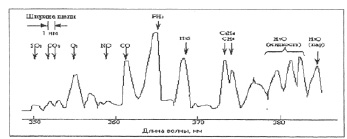
Рис. 1. Спектр комбинационного рассеяния загрязненной атмосферы
На рис. 1 показан спектр комбинационного рассеяния различных частиц, присутствующих в облаке дымового шлейфа от горящего факела. Фосфорные соединения сжигались в топке, выходящий из трубы дым был насколько слаб, что едва заметен глазом. При этом наблюдались максимумы интенсивности на длинах волн комбинационного рассеяния, соответствующих SO2, C2H4, H2CO, NO, CO, PH3, H2S, CH4, а также основным составляющим CO2, O2, N2 и H2O.
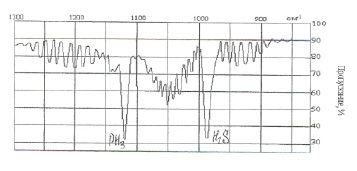
Рис. 2. Инфракрасный спектр (ИКС) фосфина и сероводорода
Комбинационный сдвиг для молекулы фосфина и сероводорода ИК – спектры записывался на ИКС-29 и представлен на рис.2. В средней ИК области фосфина и сероводорода имеют следующие полосы поглощения w1=995см-1, w2=1125см-1, которые и являются величиной комбинационного сдвига для молекулы H2S и PH3.
Постановка задачи прогноза производится, с ориентацией на распространения сероводорода и фосфина при аварийных случаях. При мощных аварийных выбросах таких высокотоксичных загрязнителей, как сероводород и фосфин, требование обеспечения экологической безопасности производств можно сформулировать в виде неравенство:
τ р < τ з – τ м (1)
где τр – время на принятие природоохранного решения, включая время решения задачи прогноза; τз – время распространения загрязнения; τм – время реализации природоохранных организаций.
Район производства предварительно разбивается на квадраты, каждому из них ставится в соответствие индекс (это может быть число, или двухмерный вектор). Решение задачи должно состоять из предупреждения: в какой момент времени тот или иной квадрат будет подвергнут опасному уровню загрязнения (направление, скорость ветра, и т.п.).
При выборе подходящей математической модели процесса распространения газообразной примеси в атмосфере необходимо учитывать, что он объединяет в себе такие различные процессы как перенос ветром, турбулентная диффузия, поглощение и химические превращения примеси. В общем процессе распространения примеси можно описать следующей дифференциальной моделью в частных производных:
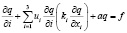(2)
где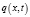 
– определенная концентрация примеси в точке 
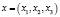в момент времени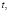 
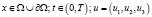– вектор скорости ветра с составляющими вдоль осей координат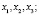 
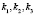– коэффициенты турбулентной диффузии вдоль соответствующих осей координат; a – коэффициент интенсивности поглощения примеси атмосферой; 
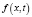– обобщенная функция, характеризующая источники выбросов на местности.
В случае наличия нескольких точечных источников функция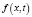 
– аппроксимируется следующим выражением
,
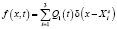где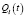 
мощность выброса ls-го источника в t-й момент времени; 
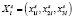– вектор координат ls-го источника. Если источник является постоянно действующим (типичным пример – трубы ТЭЦ), можно представить в виде const. Для случаев аварийных выбросов такое представление, по-видимому, неприемлемо. Здесь, в зависимости от характера аварии, можно остановиться на одном из следующих трех вариантов:
1) экспоненциальный режим
,
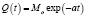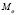– начальный выброс; а – коэффициент интенсивности выброса;
2) последующее стационирование выброса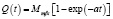 
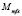– максимальная мощность выброса;
3) колебательный режим
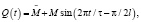
где M – амплитуда выброса.
Если обратиться к модели распространения, можно констатировать, что у нас нет надежды получить в общем виде аналитическое решения уравнения (2), то почему бы сразу не приступить к его численному решению на ЭВМ. Причина невозможности этого кроется в самой природе турбулентного потока. Решить задачу прогноза распространения, по-видимому, можно только путем разработки достаточно простой и эффективной математической модели этого процесса. Кроме того, необходимо учитывать еще одно требование, которое связано с особой опасностью сероводорода для жизни и здоровья людей. Суть его в том, что в процессе прогнозирования очень важно не пропустить опасные уровни загрязнения, пусть даже это иногда будет приводить к ложной тревоге. Общий алгоритм процесса представляется в следующей последовательности:
Вводятся дискретные данные измерений.
Производится оценка значений концентраций примеси в каждой точке дискретизации (дискретной сетки).
Решается задача прогнозирования значений концентрации примеси на Тсек времени вперед.
Задержка времени, Тсек .
Ввод замеренных концентраций примеси.
Оценка значений концентрации примеси на основе прогноза и вверенных замеренных значений.
Вычисления значения функционала J.
Если J не более заданного значения ε, то считается, что идентификация не требуется.
Если J > ε, то производится идентификация параметров; и так до тех пор, пока не выполнится условие J ≤ ε,
Если требуется прогноз для концентрации примеси на следующий интервал времени, то управление передается на п.3, если нет, то алгоритм заканчивает свою работу.
Описанный процесс доведен до программной реализации. Анализ возможности использования методов численного моделирования показывает, что этот подход имеет наиболее развитую теоретическую базу и в принципе позволяет учитывать практически все основные факторы, влияющие на процессы рассеяния.