Человек более способен усматривать свойства и особенности, характерные для геометрических объектов, чем выводить те же свойства из совокупности формул. Поэтому для более четкого понимания принципов решения задач четкого нелинейного программирования и нечеткого нелинейного программирования (ННП) аналитическими средствами важно хорошо усвоить графоаналитические методы их решения. Проблема состоит в том, что в наше время не существует общепризнанной нечеткой геометрии, которая построена на основе нечеткой логики и теории нечетких множеств.
В данной работе мы предлагаем рассмотрение графоаналитических методов решения нечетких задач нелинейного программирования с четкой нелинейной целевой функцией при нечетко заданных линейных ограничениях.
Основные понятия теории нечетких множеств, элементов нечеткой логики, нечетких соответствий и отношений, понятия нечетких геометрических объектов и нечетких геометрических фигур на плоскости будем полагать таки же как и в [1-6].
Рассмотрим такую задачу ННП: найти экстремум четкой нелинейной целевой функции:
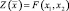(1)
при нечетких ограничениях:
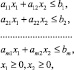(2)
где параметры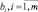 
системы (2) есть гауссовы нечеткие числа с функциями принадлежности:
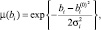(3)
где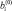 
модальные значения (ядра) нечетких чисел 
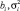– квадрат коэффициента концентрации.
Решения этой задачи ННП начинают из построения области допустимых решений (ОДР). Из графической точки зрения такая область представляет собой пересечения нечетких полуплоскостей (или нечетких прямых), которые определяются системой (2).
На этом же графике строим семейство целевых функций (1). Так как в рассматриваемом случае ОДР представляет собой нечеткий выпуклый многогранник, то в задачах такого типа нечеткая точка экстремума является вершиной такого нечеткого многогранника. Таким образом, искомое экстремальное решения, которое графически соответствует координатам нечеткой точки пересечения двух определенных нечетких прямых, можно найти путем общего решения системы двух нечетких уравнений, что соответствуют этим предельным нечетким прямым, то есть в общем случае нужно найти нечеткое решение нечеткой системы линейных алгебраических уравнений (НСЛАУ) [5].
Выразим решения НСЛАУ (2) через параметры задачи по формулам Крамера:
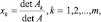(4)
где det A – определитель матрицы A = (aij), det Ak – определитель матрицы, который получается при замене k-го столбца матрицы А столбцом свободных членов (bi).
В рассматриваемом случае нечеткими являются только свободные члены bi. Значения переменных xk, что вычисляются по формуле (4), запишем, раскрывая определители det Ak по элементам k-го столбца:
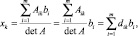(5)
где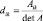 
; Aik – адъюнкта элемента aik матрицы A, k = 1, 2 ,…, n…
Теперь можно получить функции принадлежности компонентов нечеткого решения задачи [5]:
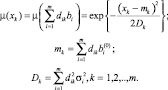
Подставив полученные значения нечетких координат точек экстремума в выражения для целевой функции (1), можно получить нечеткие значения искомой функции.
Если все неравенства нечетких ограничений преобразовать в уравнения, то получим нечеткую задачу на условный экстремум, которая может быть решена методом множителей Лагранжа.
В данной работе изложены достаточно простые графоаналитические методы определения нечетких координат нечетких экстремальных точек путем нахождения нечеткого решения НСЛАУ. Полученные в работе результаты в дальнейшем могут быть использованы для геометрической интерпретации задач нечеткого целочисленного программирования и теории нечетких игр.