Проблема применения широко реализованного нами в информатике [2, 3] принципа иерархичности для описания свойств пространства-времени рассматривался нами в [4]. Этот принцип существенно ограничивает действие господствующего в физике принципа геометризации, применимость которого не выходит за пределы отдельного пространственно-временного континуума в составе иерархически структурированного гиперконтинуума. В отличие от пространства-времени Минковского специальной теории относительности и риманова пространства-времени общей теории относительности, развиваемые нами гиперконтинуальные представления о пространстве и времени [1, 4, 5] предусматривают широкие возможности инвариантности тех или иных физических процессов относительно тех или иных групп преобразований координат. Особую роль в пространственно-временном гиперконтинууме играют преобразования Галилея, так как они при этом трактуются, как уровневые преобразования Лоренца бесконечно высокого уровня и, тем самым, позволяют единым образом синхронизировать все события во всех отдельных континуумах. В данной работе рассмотрим взаимную индукцию электрического поля магнитным полем и магнитного поля электрическим полем в пространственно-временном гиперконтинууме.
В отсутствие свободных зарядов и токов, в изотропных и однородных средах без дисперсии интегральная форма закона индукции Фарадея и теоремы о циркуляции магнитного поля имеет вид (E, B, ε, μ, c, t, s, l – напряженность электрического поля, магнитная индукция, диэлектрическая и магнитная проницаемость, скорость света в вакууме, время, двумерная открытая поверхность и ограничивающий ее замкнутый контур):
,
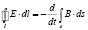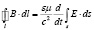. (1)
Переход от интегральной формы (1) к соответствующей дифференциальной форме тех же законов связан с представлением аргументов полевых функций. Полевые переменные E и B являются значениями полевых функций четырех пространственно-временных переменных: x, y, z (три пространственные переменные, имеющие смысл координат) и t (время). Если пространственные координаты не зависят от времени, то есть E = E (x, y, z, t), B = B (x, y, z, t), то такой переход к дифференциальной форме данных законов очевиден:
, 
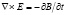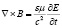. (2)
Проблема возникает в случае зависимости пространственных координат от времени:
,
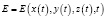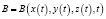, (3)
так как в этом случае математика допускает не только частные, но и полные производные полевых функций по времени. Традиционно [7] используется полная производная, что приводит к следующей формулировке законов (назовем такие законы субстанциональными):
, 
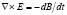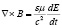. (4)
Из (4) и соответствующего закона Гаусса для электрического и магнитного полей
, 
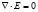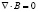(5)
в рамках преобразований Галилея при переходе от неподвижной системы отсчета, в которой напряженность электрического поля и магнитная индукция равны E и B, к подвижной (вектор скорости обозначен через v), в которой те же полевые переменные обозначим через E’ и B’, получается [7] закон взаимной индукции (назовем его глобальным)
, 
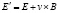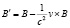, (6)
причем в [6] высказывается идея о том, что обычно вводимая в физике аксиоматически сила Лоренца имеет естественную индукционную интерпретацию посредством (6).
Но случай (3) допускает и другую формулировку закона индукции Фарадея и теоремы о циркуляции магнитного поля (назовем такую формулировку локальными законами), состоящую в совместном рассмотрении интегральной (1) и дифференциальной (2) форм, которые оказываются не эквивалентными, а взаимно дополняющими. Именно локальные законы (1)–(2) мы считаем более адекватными физической реальности, чем субстанциональные (1), (4).
Поскольку полная и частная производная полевых переменных связаны равенствами
,
,
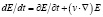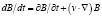одновременное выполнение (1) и (2) возможно лишь при
v → 0.
Тогда с использованием преобразований Галилея запишем (1) в виде:
,
,
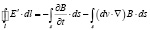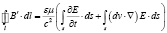а после соответствующих преобразований, аналогичных [7], с использованием правил векторного анализа и с учетом (5), получим новый закон (локальный) взаимной индукции:
, 
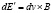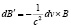. (7)
Преимуществом локального закона (7) перед глобальным (6) является то, что он позволяет получать законы преобразования электрического и магнитного полей по отдельности
, 
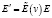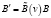
при переходе от неподвижной к движущейся системе отсчета в случае, когда для перехода от одних координат к другим используются преобразования Галилея (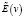
, 
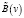– некоторые функции скорости подвижной системы отсчета относительно неподвижной).