Грунт – это минерально-дисперсное тело и обладает определенной пористостью. Изменения пористости под влиянием внешних нагрузок от сооружения подчиняются следующим закономерностям: во-первых, изменению коэффициента пористости от давления, сдвигу при трении и скольжения; ламинарной фильтрации; во-вторых, линейной или нелинейной деформируемости. Здесь при оценке сжимаемости грунтов важно выяснить зависимость между изменениями внешней нагрузки и изменением коэффициента пористости грунтов. Если неоднородная грунтовая среда в общем случае обладает свойством нелинейной ползучести, то зависимость между коэффициентом пористости и суммой главных напряжений имеет вид
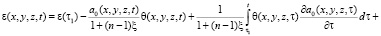
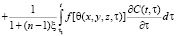, (1)
где
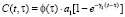, (2)
ε(t), θ(t) – эти функции также изменяются по координатам x, y, z; f[θ(τ)] – функция, характеризующая нелинейную зависимость между коэффициентом пористости ε(t) и суммой главных напряжений θ(t) в скелете грунта; φ(τ) – функция старения; a1, γ1 – параметры ползучести; t1 – момент приложения внешней нагрузки; x – коэффициент бокового давления; а0 – коэффициент сжимаемости грунта, который в общем виде может зависеть от глубины исследуемой точки и времени; п – размерность рассматриваемой задачи; C(t, τ) – мера ползучести. Причем здесь функция f[θ(τ)] может изменяться в виде
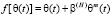. (3)
Зависимость (1) при n = 1 и (2), т.е. для одномерной задачи теории уплотнения впервые были применены В.А. Флориным [7]. Он теорию упругоползучего тела Г.Н. Маслова-Н.Х. Арутюняна [1] смог применить к описанию процесса уплотнения глинистых грунтов, обладающих свойством ползучести. Экспериментальные исследования С.Р. Месчяна [6] доказали применимость этой теории к глинистым грунтам.
Для линейной задачи теории механики уплотняемых пористых упругоползучих неоднородных грунтов зависимость (1) переходит к следующему виду
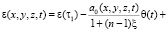
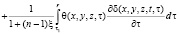, (4)
где функции f[θ(τ)] и δ(t, τ), входящие соответственно в состав формул (3) и (4), находятся из зависимостей
,
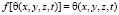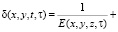
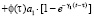. (5)
Здесь Е(x, y, z, t) – модуль деформации неоднородного уплотняемого грунта. Функция старения φ(τ), в (5), обычно представляется в виде [1, 7].
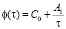, (6)
здесь С0 , А1 – опытные данные, τ – время приложения нагрузки.
Зависимости (1)-(6) будут описывать состояние скелета слабых глинистых грунтов, находящихся под давлением тех или иных внешних нагрузок. Для неоднородного упругого грунта зависимость (4) имеет вид:
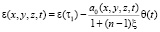. (7)
Выражение (7) для одномерной задачи теории консолидации однородного изотропного грунта имеет вид [7]
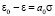, (8)
где величины ε0, a0 находятся путем эксперимента или вычислением; a0 – коэффициент сжимаемости; e0 и e – коэффициенты пористости для начального и конечного моментов времени. Причем, проф. Цытович Н.А. считал, что этот закон в механике грунтов имеет такое же большое значение, как и закон Гука в теории сопротивления материалов и коэффициент сжимаемости, а0 является очень важной характеристикой при расчете осадки сооружения.
Между коэффициентом сжимаемости а0 и модулем общей деформации Е существует зависимость [8]
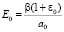, (9)
где b – коэффициент, равный для глин 0,43; для суглинков – 0,57; для супесей – 0,72; для песчаных грунтов – 0,76. Зная значение для а0 всегда из (9) можно определить Е0.
Основные разрешающие уравнения механики неоднородных упругоползучих грунтов определим следующим образом. Для этого возьмем уравнение уплотнения для пространственной задачи механики уплотняемых неоднородных грунтов без учета его ползучести, обладающих различными свойствами в вертикальном и горизонтальном направлениях
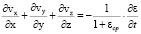, (10)
где
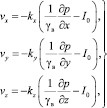(11)
откуда
, 
,
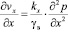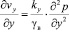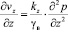, (12)
где kx, ky, kz – соответственно коэффициенты фильтрации грунта в вертикальном и горизонтальном направлениях; εср – средний коэффициент пористости в процессе уплотнения; vx, vy, vz – скорости при фильтрации воды; I0 – начальный градиент напора при фильтрации. Имея в виду (11), (12) уравнение (10) приводим к виду
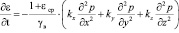.(13)
Если в место ε(t) примем (1), то
.
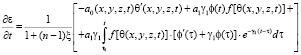Последнее соотношение, подставив в (13), находим
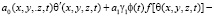
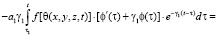
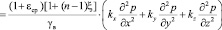. (14)
Дифференцируя последнее уравнение (14) по t, затем сложив полученное равенство с (14), предварительно умножив его на g1, получим следующее нелинейное уравнение второго порядка относительно θ(t)
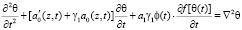, (15)
где
,
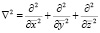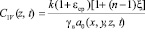, (16)
, 
, 
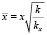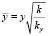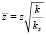. (17)
Причем для для одномерной задачи теории консолидации глинистых грунтов
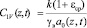, (18)
для двумерной задачи
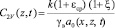, (19)
для трехмерной задачи
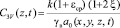. (20)
Для нахождения искомой функции θ(t), кроме граничных условий, должны быть заданы еще два начальных условий. Одно из них определяется из (14) при t = τ1 = , т.е.
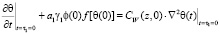. (21)
Второе начальное условие вытекает непосредственно из характера приложения нагрузки, т.е.
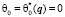. (22)
Если вместо нелинейной функции f[θ(τ)] примем (3), то нелинейное уравнение (15) имеет вид
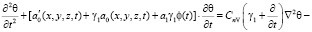
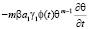. (23)
Таким образом, решение нелинейной задачи механики уплотняемых неоднородных глинистых грунтов сводится к решению нелинейного уравнения (23) при (21), (22) начальных и граничных условиях, соответствующих рассматриваемой задачи.
Рассмотрим некоторые частные случаи уравнения (23).
1. Пусть состояние скелета слабых водонасыщенных глинистых грунтов подчиняется линейной наследственной теории Г.Н. Маслова-Н.Х. Арутюняна [1, 7], т.е. уравнению (4). Тогда уравнение (23) приводится к виду
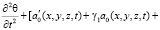
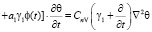. (24)
Начальные условия для уравнения (24) будут
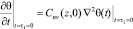, (25)
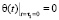. (26)
2. Если состояние скелета глинистых грунтов подчиняется закону (7), то уплотняющая среда является упругой и уравнение (23) приводится к виду
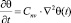. (27)
Начальное условие уравнения (27) имеет вид
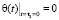. (28)
Следует заметить, что все основные уравнения механики уплотняемых водонасыщенных глинистых грунтов приведены относительно суммы главных напряжений θ(t). Можно эти уравнения представить относительно порового давления p(t). Для этого используем условие равновесия вида
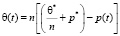. (29)
Выражение (29) подставив в уравнение (23) относительно порового давления p(t) имеем:
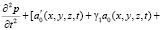
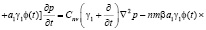
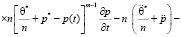
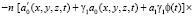
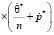. (30)
Если состояние скелета водонасыщенного уплотняемого грунта подчиняется закону (4), т.е. где учитывается его линейное свойство ползучести, то основное разрешающее уравнение механики уплотняемых глинистых грунтов имеет вид
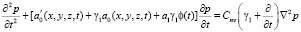. (31)
Начальными условиями для (31) будут
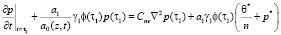, (32)
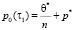. (33)
Для упругой задачи уравнение (31) имеет вид
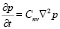, (34)
где θ*, p* – сумма главных напряжений и давление в поровой жидкости, соответствующие состоянию мгновенного уплотнения грунта.
Следует заметить, что при решении некоторых задач механики уплотняемых глинистых грунтов, связанных с расчетами вертикальных дрен, песчаными и известковыми сваями уместно использовать указанные выше уравнения (30), (34) соответственно при (32), (26) в цилиндрических координатах. Эти координаты с декартовыми ортогональными координатами связаны следующими зависимостями
, 
, 
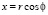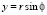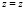. (35)
Учитывая (35) основные уравнения механики уплотняемых анизотропных по водопроницаемости глинистых грунтов (30), (31), (34), соответственно можно записать в цилиндрических координатах. При этом выражение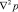 
имеет вид:
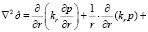
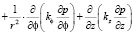, (36)
или вместо (36)
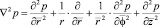, (37)
где
, 
, 
.
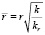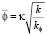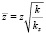Если иметь в виду, что распределение порового давления не зависит от угла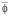 
, то вместо (37) будем иметь
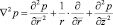. (38)
Тогда уравнение (31) при (38) имеет вид
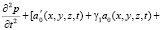
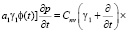
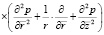. (39)
Таким образом, решив уравнения (30), (31), (34) (39) при соответствующих краевых условиях находим решение той или иной задачи теории консолидации земляных масс.
В качестве иллюстрации решим уравнение (31) применительно к одномерной задачи теории уплотнения неоднородных упругоползучих грунтов. Неоднородность грунта по Г.К. Клейну [5] с глубиной уплотняемого массива изменяется согласно закону:
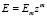, (40)
где Em – модуль деформации на глубине z = 1; m – показатель неоднород-ности основания, который связан с коэффициентом Пуассона μ0 так μ0(2 + m) = 1. В отличие от (40), в данной работе модуль деформации грунта будет принят в виде
(
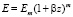
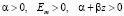), (41)
где Em, a, b, m являются опытными параметрами.
Рассмотрим уплотнение слоя неоднородного водонасыщенного грунта мощностью h, залегающего под песчаной подушкой. В начальный момент времени (t = 0) к слою грунта мгновенно прикладывается равномерно распределенная нагрузка q. Величина избыточного порового давления p(z, t) при t = 0 будет равна
,
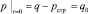т.е. часть нагрузки, равная величине структурной прочности сжатия рстр, сразу же воспринимается скелетом грунта.
Если модуль деформации уплотняемого грунта изменяется по глубине, подчиняясь закону (41), а старение грунта не принимается во внимание, то уравнение одномерной задачи механики водонасыщенных глинистых грунтов при n = 1 будет иметь следующий вид:
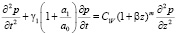. (42)
Начальными условиями для этого уравнения будут:
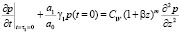, (43)
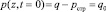. (44)
Следует заметить, что при выводе этих соотношений мера ползучести уплотняемого водонасыщенного глинистого неоднородного грунта была принята в виде
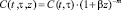. (45)
При модифицированном законе Дарси граничные условия исследуемой задачи примут вид:
, 
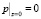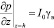. (46)
Решение уравнения (42) при граничных (46) условиях получим в виде следующей формулы
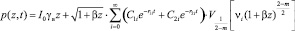. (47)
Здесь функция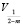 
зависит от величины 
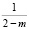. Если она целая, то
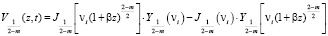, (48)
если же дробная, то
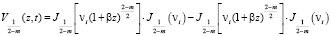. (49)
r1i, r2i – решение следующего уравнения
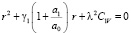. (50)
Параметр l находится из следующего трансцендентного уравнения:
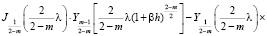
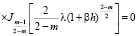. (51)
Коэффициенты C1i, C2i определены из выражения (43) и (44), т.е.
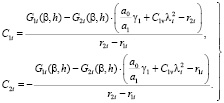, (52)
где
, 
,
, 
,
, 
.
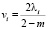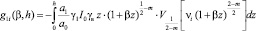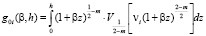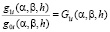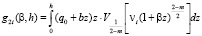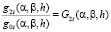Значения давлений в поровой жидкости в момент времени, сколь угодно близкий к моменту приложения нагрузки, определяются выражением
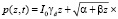
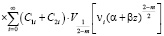. (53)
После определения давлений в поровой жидкости напряжения в скелете грунта вычисляется по следующей расчетной формуле
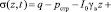
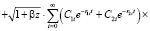
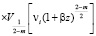. (54)
Выражение (54) дает возможность определить расчетную формулу для вычисления вертикальных перемещений точек верхней поверхности неоднородного глинистого основания из выражения:
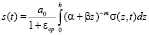. (55)
Если обозначим отношение осадки s(t) уплотняемого слоя грунта для любого момента времени t к полной стабилизации осадки sµ через u, то оно равно
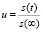, (56)
где
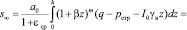
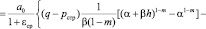
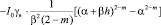. (57)
Учитывая выражения (55) и (57), после несложных математических преобразований выражение (56) находим в виде:
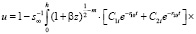
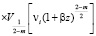. (58)
Выражение u называется степенью консолидации для любого момента времени. Тогда осадку слоя грунта можно вычислить по следующей формуле
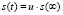. (59)
Таким образом, чтобы вычислить поровое давление p(z, t), напряжение в скелете грунта σ(z, t) и осадку уплотняемого водонасыщенного глинистого грунта s(t), используем расчетные формулы (53) – (59).
В качестве иллюстрации полученных теоретических решений рассмотрены примеры для случаев m = 1 и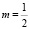 
.
Анализ расчетных формул дает, что поровое давление зависит от проницаемости, уплотняемости и скорости нарастания ползучих деформаций грунта. Причем при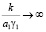 
давление в воде равно нулю. При 
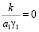в момент времени t = 0, p = q0 = q – pстр. При промежуточном значениях величины 
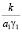имеет место промежуточное состояние, причем эпюры начальных давлений не прямолинейны в отличие от случая, когда 
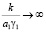. Для моментов времени t → µ величина давления стремится к I0γвz. Для любого промежуточного момента времени имеем, что при k = 0 p = q0 (z, t). Откуда следует, если бы грунт был сжимаемым и одновременно водопроницаемым, то нагрузка не полностью воспринималась бы только водой. Если k → µ, то p (z, t) = I0γвz, а при γ1 → µ решение задачи совпадает с обычным её решением.
Следует заметить, что подобные задачи в иных постановках, авторами данной работы, также исследованы в [2–4].