Проблема применения широко реализованного нами в информатике [2] принципа иерархичности для описания свойств пространства-времени рассматривался нами в [3]. Этот принцип существенно ограничивает действие господствующего в физике принципа геометризации, применимость которого не выходит за пределы отдельного пространственно-временного континуума в составе иерархически структурированного гиперконтинуума. В отличие от пространства-времени Минковского специальной теории относительности и риманова пространства-времени общей теории относительности, развиваемые нами гиперконтинуальные представления о пространстве и времени [1] предусматривают широкие возможности инвариантности тех или иных физических процессов относительно тех или иных групп преобразований координат. Особую роль в пространственно-временном гиперконтинууме играют преобразования Галилея, так как они при этом трактуются, как уровневые преобразования Лоренца бесконечно высокого уровня и, тем самым, позволяют единым образом синхронизировать все события во всех отдельных континуумах. В данной работе рассмотрим индукцию электрическим полем самого себя в гиперконтинуальном вакууме, то есть «пустой» от реальных частиц области пространственно-временного гиперконтинуума.
В формулах будем использовать тензорную нотацию (с соглашением суммирования Эйнштейна), при этом индексы, варьирующиеся от 0 до 3, будем обозначать латинскими буквами, а от 1 до 3 – греческими. Электромагнитное поле описывается в конкретной инерциальной системе отсчета своими полевыми функциями (их значения называют полевыми переменными), представляющими собой вещественнозначные функции 4-вектора события x = (xn) = (x0, r) = (ct, xa), где r, c, t, xa – радиус-вектор, скорость света в вакууме, время, прямоугольные декартовы пространственные координаты. В случае вакуума используются две полевые переменные E = E(x), B = B(x) – напряженность электрического поля и магнитная индукция. Одну из них можно исключить, перейдя от уравнений Максвелла к волновому уравнению для другой (оставим E). При этом традиционно все компоненты xn считаются независимыми переменными полевых функций. Введем 3-векторы безразмерной скорости v (va) и приращения безразмерной скорости Dv (Dva), а также 4-вектор 4-скорости u = (un) = (u0, v) = (1, va), где ua = va, un = dxn/dx0, Dva = const. Преобразование Галилея с параметром Dv с задержкой на время t0 переводит событие x в исходной (нештрихованной) системе отсчета в событие x’ = (x’n) = (x’0, r’) в штрихованной инерциальной системе отсчета, причем x’0 = x0, r’ = r + (x0 – ct0)Dv. Для определения закона преобразования поля при преобразовании Галилея нужно вместо функции E(x) ввести полевую функцию E’(v, x). Тогда если в нештрихованной системе отсчета полевая переменная имела вид E = E’(v, x), то в штрихованной она примет вид E’ = E’(v + Dv, x’).
Из уравнений Максвелла в дифференциальной и интегральной формах следуют одноименные формы волнового уравнения (S – двумерная открытая поверхность, Dv = 0):
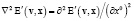 ,
,
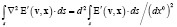 .
.
В предположении Галилей-инвариантности волнового уравнения имеем для любого v:
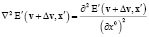 ,
,
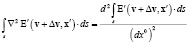 .
.
Если t0 = x0/c, то r’ = r, x’ = x, тогда из данного волнового уравнения получим:
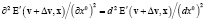 .
.
Выполнение этого равенства для любого v возможно лишь при Dv → 0. Тогда имеем:
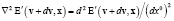 . (1)
. (1)
Правую часть (1) найдем, как полную производную, а левую – с помощью ряда Тейлора:
 ; (2)
; (2)
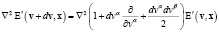 . (3)
. (3)
Подставим (2) и (3) в (1) и приравняем коэффициенты при одинаковых дифференциалах:
۞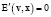 , (4)
, (4)
۞ = (۞nm); ۞nm 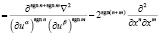 , (5)
, (5)
где ۞ – новый дифференциальный оператор, который назовем оператором Дубровина.
Оператор Дубровина ۞ (5) обобщает оператор Даламбера □, который оказывается одной из его десяти компонент, так как при n = m = 0 имеем: ۞ = □.
В случае плоской волны (напряженность поля зависит от x0 и x1, но не зависит от x2 и x3), зависящей от v1, но не зависящей от v2, v3, из (4), (5) имеем систему уравнений:
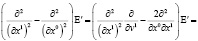
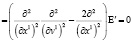 . (6)
. (6)
Новое одномерное однородное гиперконтинуальное волновое уравнение (6) с известным одномерным однородным волновым уравнением в качестве первой компоненты представляет собой частный случай нового однородного гиперконтинуального волнового уравнения (4). Найдем удовлетворяющие (6) плоские монохроматические волны вида
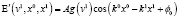 ,
,
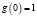 ,
,
где k0 ≥ 0, k1 ∈ ℝ, φ0 ∈ ℝ, а A – амплитуда при v1 = 0. Решение имеет вид:
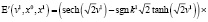
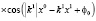 .
.

