В данной работе рассматривается регуляризация с малым параметром нестационарной модели несжимаемой жидкости в переменных функции тока и вихря скоростей. Получено существование и сходимость обобщенного решения приближенной задачи, а также выведены равномерные априорные оценки и оценка скорости сходимости решения.
Рассмотрим уравнения вязкой несжимаемой жидкости в форме Ламба-Громека:
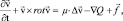
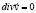(1)
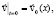
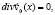
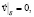(2)
где x = (x1, x2, x3),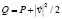 
– полный напор, область W ⊂ R3 – прямоугольный параллелепипед.
В работах [1], [3] предложены некоторые численные методы решения задач (1)–(2) в переменных «функция тока – вихрь скоростей». В [3] показано эквивалентность двух задач. Рассмотрим задачу (1)–(2) в переменных «функция тока – вихрь скоростей»:
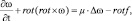
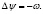(3)
Пусть часть границы области лежит на оси x1 = 0. Тогда начально-краевые условия преобразуются следующим образом:
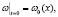
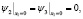
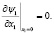(4)
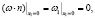
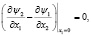
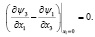(5)
Система уравнений (3) не является системой Коши-Ковалевской, поэтому непосредственное применение метода дробных шагов затруднительно. Одним из способов решения рассматриваемой задачи – аппроксимация системы уравнений (3) уравнениями эволюционного типа. Тогда исходная система уравнений с малым параметром имеет вид:
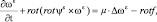
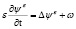(6)
с начально-краевыми условиями:
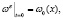
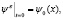
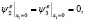
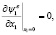
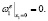(7)
Определение обобщенного решения задач (6), (7) дается аналогично [4].