В данной работе показывается получение основных уравнений гидродинамики [1] в рамках формальной единой структуры, определяемой координатами Эйлера.
Для описания состояния некоторой системы используется произвольная функция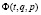 
в координатах Эйлера 
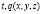и 
.
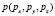Эволюция систем во времени обеспечивается полной производной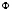 
по времени:
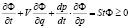, (1)
где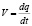 
− скорость, 
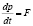− сила и 
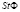− интеграл столкновений, формализующий эволюцию систем из равновесного состояния в неравновесное состояние и обратно. Так при 
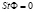система находится в состоянии равновесия, при 
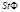>0 − система неравновесна.
Уравнение непрерывности. В данном случае в (1) возможно аппроксимация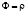 
как плотности массы при 
:
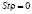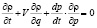, (2)
где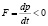 
− сила; 
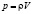− импульс. Тогда выражение (2) примет вид
.
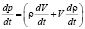Поскольку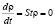 
, то второе слагаемое 
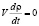. Следовательно, 
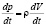. При подстановки данного выражения в (2) и с последующим использованием теоремы о перебросе производной, получим
.
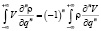При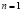 
приводим (2) к уравнению непрерывности:
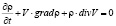. (3)
В сокращенном виде:
,
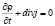где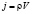 
− плотность потока жидкости.
Уравнение движения в гидродинамике. Решение данной задачи требует в (1) представления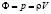 
как гидродинамического импульса. При этом 
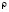− плотность жидкости. Тогда
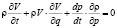. (4)
В гидродинамике, силу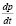 
представляют в виде градиента давления 
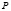если движение жидкости происходит только лишь под действием давления 
:
.
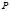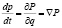Для движения реальной жидкости надо учитывать еще и гравитационную силу Ньютона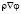 
, где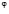 
− потенциальная энергия единицы массы жидкости и силу сопротивления в виде силы вязкости 
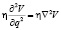, где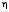 
− вязкость. Для многих задач, особенно при малых скоростях 
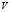, можно считать жидкость несжимаемой 
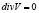. При этих условиях, уравнение движения приобретает следующий вид:
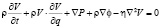. (5)
Данное выражение можно представить в форме:
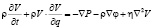. (6)
Уравнение Навье-Стокса. Данное уравнение является основным в гидродинамике. Оно описывает зависимость скорости движения жидкости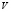 
от различных факторов, рассмотренных выше. Очевидно, что (6) можно дать в виде:
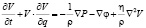, (7)
где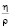 
− удельная вязкость. Для вывода уравнения Навье-Стокса необходимо воспользоваться некоторыми правилами векторного анализа для слагаемого 
:
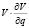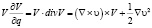. (8)
Здесь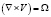 
− векторный потенциал вихревого поля скорост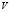и 
и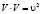 
− скалярное произведение двух векторов 
.
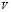Таким образом, равенство (7) можно представить, с учетом (8), в стандартной форме уравнения Навье-Стокса:
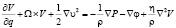. (9)
Уравнение Бернулли. Это уравнение описывает стационарный поток жидкости при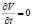 
, отсутствии турбулентности 
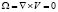и силы вязкости 
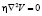. Тогда упрощение по 
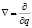уравнения (9) дает уравнение или теорему Бернулли:
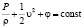. (10)
Уравнение Эйлера. Данное уравнение является уравнением идеальной жидкости, для которой в выражении (9):
,
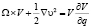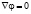и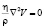 
.
Таким образом,
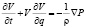. (11)
Уравнение гидростатики. Гидростатика предполагает, что в выражении (9) во всех слагаемых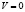 
. Тогда оно приобретает вид:
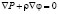. (12)
Таким образом, все базовые уравнения гидродинамики имеют одну и ту же формальную основу в виде соотношения (1).