Проблема применения широко реализованного нами в информатике [2, 3] принципа иерархичности для описания свойств пространства-времени рассматривался нами в [8]. Этот принцип существенно ограничивает действие господствующего в физике принципа геометризации, применимость которого не выходит за пределы отдельного пространственно-временного континуума в составе иерархически структурированного гиперконтинуума. В отличие от пространства-времени Минковского специальной теории относительности и риманова пространства-времени общей теории относительности, развиваемые нами гиперконтинуальные представления о пространстве и времени [1, 4-9] предусматривают широкие возможности инвариантности тех или иных физических процессов относительно тех или иных групп преобразований координат. Особую роль в гиперконтинууме играют преобразования Галилея, так как они при этом трактуются, как уровневые преобразования Лоренца бесконечно высокого уровня и, тем самым, позволяют единым образом синхронизировать все события во всех отдельных континуумах. В данной работе рассмотрим индукцию электрического поля магнитным полем в пространственно-временном гиперконтинууме.
Закон индукции Фарадея (назовем его локальным) в дифференциальной и интегральной формах традиционно записывается в виде:
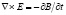, (1)
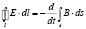, (2)
где E, B, t, s, l – напряженность электрического поля, магнитная индукция, время, двумерная открытая поверхность и ограничивающий ее замкнутый контур.
В [10] введен новый закон индукции Фарадея (назовем его субстанциональным), имеющий ту же интегральную форму (2), но другую дифференциальную форму:
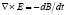. (3)
В [10] из закона (2), (3) и закона Гаусса для магнитного поля в дифференциальной форме
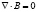(4)
в рамках преобразований Галилея при переходе от неподвижной системы отсчета, в которой напряженность электрического поля и магнитная индукция равны E и B, к подвижной (вектор скорости обозначен через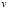 
), в которой напряженность электрического поля обозначим через 
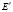, получен закон магнитоэлектрической индукции (назовем его глобальным)
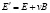, (5)
посредством которого ранее вводимая в физике аксиоматически сила Лоренца получает естественную индукционную интерпретацию.
Несмотря на такой успех субстанционального закона индукции Фарадея в объяснении физического механизма возникновения силы Лоренца, его введение нам не представляется научно обоснованным. Мы считаем необходимым рассматривать магнитоэлектрическую индукцию в пространственно-временном гиперконтинууме, исходя из локального закона индукции Фарадея.
Поскольку в силу известной связи между субстанциональным и локальным дифференцированием выполнено равенство
,
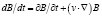одновременное выполнение (1) и (2) возможно лишь при
.
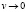Тогда для подвижной системы отсчета с использованием преобразований Галилея запишем (2) в виде:
,
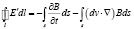а после соответствующих преобразований с использованием известных правил векторного анализа в итоге получим:
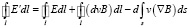.(6)
Из (6) с учетом (4) получаем новый закон магнитоэлектрической индукции, который назовем локальным:
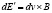. (7)
Сравнение (5) и (7) позволяет сделать соответствующие выводы относительно сходства и различия глобального и локального законов магнитоэлектрической индукции. Закон (5) является более жестким, чем (7), так как (7) получается из (5) дифференцированием, а из (7) не обязательно следует (5). Тем не менее, закон (7) так же объясняет физический механизм возникновения силы Лоренца, как и закон (5). Однако преимуществом закона (7) перед законом (5) является то, что он позволяет в совокупности с подходящим локальным законом электромагнитной индукции получать строго математически соответствующие законы преобразования электромагнитного поля при переходе от одной системы отсчета к другой в случае, когда для перехода от одних координат к другим используются преобразования Галилея.