Рассмотрим строение простейших кристаллов, которые построены из атомов одного типа. Наиболее распространены три типа кристаллических решеток (кубическая гранецентрированная, объемноцентрированная кубическая, плотнейшая гексагональная). В описанных трех решетках кристаллизуется множество элементов: Be, Co, Al, Cu, Cr, Fe и т.д.. Из других структур упомянем структуру алмаза и графита. Для структуры алмаза характерно то, что атом углерода имеет четыре ближайших соседа.
Применительно к механике сплошной среды соответствующий математический аппарат был развит вначале в теории турбулентности [1 – 4] в рассеянии волн в неоднородной атмосфере. В годы после второй мировой войны развитие авиации, атомной энергетики, ракетно – космической техники выдвинуло новые постановки задач тепло – массообмена и вместе с тем – новые, более жесткие требования к полноте и надежности данных теории и эксперимента.
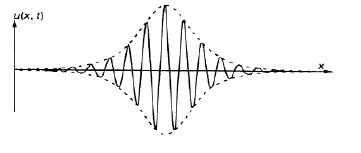
Пример групповых солитонов (штриховая линия)
При исследовании турбулентных движений традиционным является представление мгновенного значения скорости ( или скалярной компоненты – температуры, концентрации) в виде ее среднего значения и некоторого отклонения от среднего (пульсации) . За последнее время сфера интенсивного исследования и применения явлений тепло – массообмена чрезвычайно расширилась. Она включает как ведущие направления техники ( химическая технология, металлургия, строительное дело, нефтепереработка, машиностроение, агротехника и т.д.), так и основные естественные науки ( биология, геология, физика атмосферы и океана и др.).
В океанических течениях при больших числах Re использовались численные методы, разработанные для поведения бесконечно малых возмущений на основе линеаризованных гидродинамических уравнений. В последнее время для отдельных классов течений делаются попытки прямого численного моделирования переходных и турбулентных режимов на основе нестационарных уравнений Навье – Стокса. Отдельные решения уравнений Навье – Стокса имеют вид (рисунок) групповых солитонов. Другие явления в турбулентных потоках описываются теорией случайных функций.
В настоящее время теория случайных функций широко используется для решения самых разнообразных задач механики твердых деформируемых тел: расчет на прочность при случайных воздействиях, прогнозирование надежности с учетом случайных факторов, исследование влияния случайных неровностей поверхности на деформированное состояние, изучение деформации тел со случайными неоднородностями и определение их эффективных характеристик.

