Умения проводить доказательные рассуждения входят в число основных интеллектуальных умений. Ведущая роль в формировании этих умений принадлежит геометрии, однако, как показал анализ школьной практики, успех в этой работе в значительной степени предопределен готовностью учащихся уже в начале курса выполнять различные виды деятельности, связанные с проведением доказательных рассуждений. Готовить школьников к проведению доказательных рассуждений следует уже в курсе математики V-VI классов, но эту работу следует проводить и в VII-IX классах.
Следуя А.Н. Капиносову [7], мы под рассуждениями (проведением рассуждений) понимаем мыслительную деятельность, направленную на решение определенных задач, состоящую из актуализации некоторых ранее известных субъекту суждений и выполняемых на их основе переходов от одних суждений к другим. Под доказательными рассуждениями понимаются такие, в которых основаниями перехода от одних суждений к другим являются теоретические предложения (аксиомы, теоремы, определения некоторой математической теории).
В методической литературе выделяют четыре уровня проведения доказательных рассуждений:
– простого воспроизведения (предъявленная задача распознается субъектом, как ранее решенная и рассуждение представляет воспроизведение известного);
– обобщенного воспроизведения (рассуждение проводится на основе выделения общего в условии и требовании предъявленной задачи и ранее решенной или на основе распознавания задачи как принадлежащей к типу задач с известной схемой рассуждения);
– логического поиска (решение задачи отыскивается на основе выполнения действий выведения следствий и отыскания достаточных условий);
– логико-эвристический (выполнение действий выведения следствий или отыскания достаточных условий связано с применением различного рода эвристик).
Первые два уровня являются репродуктивными, а последние два – продуктивные. На уровне V-VI классов учащихся надо учить проводить доказательные рассуждения на первых трех уровнях, четвертый уровень относится к более поздним ступеням обучения. Обучать учащихся умениям доказательно рассуждать в V-VI классах надо в основном на числовом материале, ибо он занимает в этом курсе значительный удельный вес и он логически относительно прост. В свое время А.И. Маркушевич отмечал: «Логическая структура арифметических и алгебраических вопросов и задач, как правило, является простой, отчетливой, поэтому их следует в значительно большей мере, чем это делалось до сих пор, привлекать в целях математического воспитания» [8, с.40].
Приведем примеры некоторых заданий, на которых может строиться работа по формированию у учащихся умения проводить доказательные рассуждения, но прежде на двух задачах покажем, как должен строиться ответ школьников.
Задание 1. Число а – отрицательно. Положительным или отрицательным числом будет (–8 + а)? Ответ обосновать.
Ответ: Число (-8 + а) – отрицательно, так как сумма отрицательных чисел – число отрицательное.
Задание 2. Может ли значение выражения 2аb – а – 3b быть отрицательным при отрицательных значениях а и b? Ответ обосновать.
Ответ: Нет, ни при каких отрицательных значениях а и b значение указанного выражения не может быть отрицательным, так как при любых отрицательных значениях а и b каждое слагаемое выражения (2аb; –а; –3b) есть число положительное, а сумма положительных чисел всегда есть число положительное.
Укажем еще ряд заданий подобного характера.
1) Числа а + р и а равны. Какое число обозначено буквой р? Ответ обосновать.
2) а + b = р, b + а = k. Могут ли буквы р и k обозначать различные числа? Ответ обосновать.
3) а – b = р. Является ли число р разностью чисел а + m и b + m? Ответ обосновать.
4) Число а делится на число b, число k не делится на b. Делится ли число аk на b? Ответ обосновать.
5) Число а делится на число b, число k не делится на b. Делится ли число а + k на b? Ответ обосновать.
6) При делении числа а на 12 получим в остатке число 15. Правильно ли выполнено деление?
7) Доказать, что число 37 является делителем всех трехзначных чисел, записанных одинаковыми цифрами.
8) Число b кратно 15. Доказать, что число b кратно 3.
9) а = 30b. Какой цифрой оканчивается запись числа а? Ответ обосновать.
10) Для записи числа использованы только цифры 3, 7, 8. Делится ли это число на 5? Ответ обосновать.
11) Для записи числа использованы только цифры 0 и 5. Делится ли это число на 5? Ответ обосновать.
12) Верно ли утверждение: любое натуральное число является простым или составным? Ответ обосновать.
13) Доказать, что числа 21 и 55 взаимно простые числа. Ответ обосновать.
14) Могут ли два различных четных числа быть взаимно простыми? Ответ обосновать.
15) Запись числа а оканчивается цифрой 0, число b – цифрой 5. Могут ли числа а и b быть взаимно простыми? Ответ обосновать.
16) На координатной прямой отмечены точками С и А числа 7 и а так, что ОС ≠ ОА. Являются ли числа 7 и а противоположными? Ответ обосновать.
17) Может ли число |b| изображаться на координатной прямой точкой, которая лежит слева от начала отсчета? Ответ обосновать.
18) Числа а – 4 и |а – 4| равны. Положительным или отрицательным является число а – 4, если известно, что а – 4 ≠ 0? Ответ обосновать.
19) Число а отрицательное. Какое из чисел больше b + а или b? Ответ обосновать.
20) Два числа отмечены на координатной прямой точками, которые лежат по одну сторону от начала отсчета. Может ли сумме чисел соответствовать точка, которая лежит с другой стороны от начала отсчета? Ответ обосновать.
21) Может ли число 5 быть суммой двух отрицательных чисел? Ответ обосновать.
22) Модулем чисел а и b являются соответственно числа -а и -b. Положительным или отрицательным является число а + b? Ответ обосновать.
23) Число b ≠ 0. Положительным или отрицательным является число b, если 7b = –7|b|? Ответ обосновать.
24) Для чисел а, b, с, k, выполняются равенства 5а = с, 5b = k. Сравнить дроб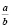и 
и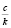 
. Ответ обосновать.
25) Доказать, что взаимно обратные чисел не могут иметь различные знаки.
26) На координатной прямой по разные стороны от начала отсчета отмечены точками числа а и b. Могут ли числа а и b быть взаимно обратными? Ответ обосновать.
27) Обосновать равенство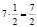 
, не выполняя вычислений.
28) Доказать, что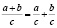 
.
29) Доказать, что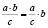 
.
30) а + с = а. Могут ли числа а и с быть взаимно обратными? Ответ обосновать.
Как показал анализ школьной практики, умения доказательно рассуждать не приобретаются учащимися спонтанно, их нужно целенаправленно формировать и развивать посредством специально подобранных задач. М.Е. Драбкина и И.Л. Никольская отмечают: «Если ограничиться только разбором образцов доказательств в классе и решением обычных (предлагаемых учебником) задач на доказательство, то только у отдельных, лучших учащихся стихийно вырабатываются соответствующие приемы мыслительной деятельности, но они не достаточно осознаются ими как общие приемы. Большинство же учащихся беспомощны, когда им приходится самим решать задачи на доказательство» [6, с. 6].
На пропедевтическом уровне школьников следует учить строить не только индуктивные, но и дедуктивные рассуждения, они-то и будут впоследствии положены в основу доказательства теорем. Рассмотрим два примера дедуктивных рассуждений.
Пример 1. Докажите, что числа а = –135 и b = –207 не обращают в нуль выражение
.
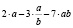Индуктивное рассуждение основывалось бы на непосредственной подстановке указанных значений а и b в выражение (значение выражения будет отлично от нуля).
Дедуктивное обоснование того, что а = –135 и b = –207 не обращают в нуль заданное выражение будет строиться следующим образом.
При подстановке в заданное выражение любых отрицательных значений а и b, каждое слагаемое этого выражения (2а;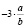 
; –7аb) будет отрицательным числом, которые в сумме не могут дать нуль. Так как числа а = –135 и b = –207 отрицательны, то и они не обращают в нуль заданное выражение.
Пример 2. Рассмотрим, каким образом можно в курсе математики VI класса дедуктивно построить изложение вопроса о нахождении расстояния между двумя точками на координатной оси (этот вопрос в школьном учебнике изложен конкретно-индуктивным методом).
Центральным в курсе математики является само понятие расстояния между двумя точками, а нахождение расстояния между двумя точками на координатной оси – вопрос все же частный. В нашем изложении будем отталкиваться от общего понятия – расстояние между двумя точками.
Прежде, учащимся уже предлагались различные способы измерения расстояния между двумя точками: с помощью масштабной линейки, с помощью циркуля и масштабной линейки (в систематическом курсе геометрии будут даны и другие способы, в частности, основанные на теореме Пифагора, теоремах синуса и косинуса).
Для нахождения расстояния между двумя точками может быть использована координатная ось. Наложим координатную ось на две заданные точки. При этом возможны три разных случая (рисунок).
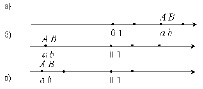
а) Точки А и В оказались по правую сторону от начала отсчета (а > 0, b > 0).
б) Точки А и В оказались по разные стороны от начала отсчета (а < 0, b > 0).
в) Точки А и В оказались по левую сторону от начала отсчета (а < 0, b < 0).
Заметим, что в каждом из трех случаев точки займут на координатной оси одно определенное место, которое характеризуется координатой точки.
Для нахождения длины отрезка АВ в случае рис. 1 а, поступим следующим образом:
АВ = ОВ – ОА = b – а.
Для нахождения длины отрезка АВ в случае рис. 1 б, следует поступить так:
АВ = ОВ + ОА= b + |а| = b – а
(при раскрытии |а| знак поменялся на противоположный, так как число а отрицательно).
Для нахождения длины отрезка АВ в случае рис. 1 в, поступим так:
АВ = ОА – ОВ = |а| – |b| = =–а – (–b) = -а + b = b – а
(при раскрытии |а| и |b| знак менялся на противоположный, так как числа а и b отрицательны).
Итак, для нахождения расстояния между двумя точками на координатной оси, следует из координаты правой точки вычесть координату левой точки.
Затем, рассмотрев свойство модуля, а именно: |а – b| = |b – а|, учащимся можно сообщить, что длина отрезка АВ выражается формулой АВ = |а – b| = |b – а|.
Более обстоятельный разговор о поднятой в статье проблеме читатель найдёт в наших работах [1, 2, 3, 4, 5].