Фактор времени в экономике информационного общества приобретает всё большее значение. Процессы глобализации и усиливающейся конкуренции экономик стран мира приводят к увеличению рисков и нестабильности на всём мировом экономическом пространстве. Опоздание или досрочное принятие управленческого решения может привести к нежелательным последствиям для экономической системы, неэффективной затрате её ресурсов или даже кризису. Под экономической системой мы будем понимать экономику страны, региона, отрасли, корпорации и т.п.
Рассмотрим на простом примере задачу выбора времени для принятия управленческого решения (действия), с условием, чтобы вследствие этого был достигнут наибольший ожидаемый эффект. Пусть перед нами стоит задача раскачать тяжёлый колокол, т.е. увеличить амплитуду его колебаний. Траектория колебаний колокола во времени представлено на рис. 1.
Чтобы с наименьшими затратами усилий (ресурсов) увеличить амплитуду или раскачать колокол, т.е. получить наибольший эффект, надо прикладывать усилие в момент времени t1. Если прикладывать усилия с периодом, совпадающим с периодом гармонических колебаний колокола, то даже слабые воздействия вызовут сильный отклик системы, т.е. мы будем иметь явление резонанса.
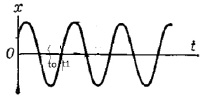
Рис. 1. Гармоническое колебание колокола
На рис. 2 отображена динамика индекса предпринимательской уверенности (ИПУ) в сфере услуг по . Российской Федерации.
Колебательный характер этого индекса очевиден. Очевидно также, что внешнее воздействие в определённые периоды времени могут увеличивать (подталкивать) или уменьшать значение этого индекса, в то время как в другое время эти внешние воздействия не приведут к желаемому результату. К числу таких внешних воздействий можно отнести, например, какие-то действия Правительства (изменение налогового или инвестиционного законодательства, заключение контрактов с крупными зарубежными заказчиками и т.д.) или внешнего мира (санкции). По аналогии с предыдущим примером, если мы захотим повысить ИПУ, то необходимые действия принесут наибольший ожидаемый эффект, если они будут предприняты в момент времени перехода ИПУ из отрицательной фазы в положительную.
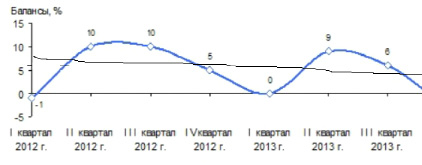
Рис. 2. Динамика индекса предпринимательской уверенности в сфере услуг [1]
Конечно, динамика многих экономических показателей не всегда демонстрирует явный колебательный характер. Но любой график можно представить как сумму гармоник из разложения функции графика в ряд Фурье. При этом некоторым гармоникам, возможно, можно дать экономическую интерпретацию. Воздействую на эти гармоники определённым образом, можно получить тот или иной эффект в зависимости от времени воздействия.
Но при этом мы предполагаем, что «картинка» и в будущем не изменится, т.е. мы опираемся на исторические данные. Но в экономике часто происходят неожиданные, случайные события, которые приводят к фазовым сдвигам, появлению дополнительных гармоник и т.д. и т.п. Таким образом, что бы выбрать момент начала действий, в данном случае, для увеличения ИПУ, модель должна включать в себя и вероятности появления существенных событий, т.е. таких событий, которые могут повлиять на характеристики системы.
Для определения времени принятия решения только на основе анализа колебательных или циклических составляющих динамики экономического процесса необходима уверенность в стабильности или устойчивости параметров этих колебаний. Такая стабильность, наблюдается, например, в сезонных колебаниях и время принятия решений на их основе определяется вполне достоверно. Например, выдавать субсидии фермерам, наверное, следует ранней весной, а закупать урожай скорее всего надо осенью. Суточные колебания также приводят к выводу, что, скорее всего решение надо принимать днём, а не в ночное время суток. В более сложных случаях, когда не прослеживаются сезонные или суточные колебания, динамика экономических процессов может содержать гармоники, которые потребуют своего обоснования и исследования.
Для принятия нужного решения по управлению экономической системой именно в нужное время, необходимо опираться на глубокое знание самой экономической системы, качественную экономико-математическую модель и на достоверную информацию о возможных внешних воздействиях на неё.
Традиционно прогнозированием поведения экономической системы во времени занимается эконометрика на основе моделей временных рядов.
Несмотря на очевидные успехи эконометрики в объяснении и предсказании поведения экономических систем и процессов во времени, многие учёные и практики не удовлетворены результатами её применения и даже считают её лженаукой или, по крайней мере, бесполезной. Наиболее известные и дальновидные экономисты давно уже критиковали эконометрику. Например, великий американский экономист Кейнс считал, что прогноз в экономике невозможен, так как экономическая среда изменчива и непредсказуема, а большинство экономических переменных связано между собой множеством сложных нелинейных зависимостей. [2]. В начале 1970-х годов известный английский экономист Уорсвик резко критиковал экономистов-математиков за несовпадение выводов, полученных на основе моделей, с конкретными фактами [3]. В. Леонтьев охарактеризовал эконометрику как «попытку компенсировать бросающийся в глаза недостаток имеющихся данных путем широко использования все более и более изощренных статистических приемов» [4]. Резко отрицательно к эконометрике относились и представители австрийской школы экономики [5, 6].
В настоящее время появились предпосылки преодоления указанных выше недостатков эконометрик как за счёт более глубокого понимания сущности происходящих в экономике процессов, главными из которых мы считаем информационные, так и за счёт колоссальных возможностей сбора и обработки информации, имеющихся у современных информационных технологий [7]. Всё это даёт основание для постановки проблемы получения принципиально нового знания о времени принятия управленческого решения с целью получения наибольшего эффекта от его реализации. Науку, которая будет этим заниматься, мы называем хроноэкономикой.
Представляя в хроноэкономике экономическую систему и происходящие в ней процессы в виде модели, мы исходим из того, что её ключевые показатели, изменяясь во времени, обладают волновыми свойствами и в то же время эти изменения носят неопределённый, вероятностный характер. Вероятности тех или иных изменений ключевых показателей, в свою очередь, определяются вероятностями тех существенных событий, которые могут на них повлиять. Как сами эти события, так и информационные сигналы о наступлении этих событий воздействуют на ключевые показатели экономической системы и порождают другие события, которые также могут влиять на экономическую систему.
Необходимость учёта влияния информационных сигналов в моделях экономики информационного общества сегодня является общепризнанной. Хотя ещё в 30-х годах прошлого века Ральф Нельсон Эллиотт [8] считал, что информационная составляющая жизни общества является главной причиной волнового движения рынков. Теория волнового движения рынков была предложена им в 30-х годах. Изучая графики, он заметил, что цены на биржевых рынках развиваются по определённой модели. Математической основой теории Эллиотта, по признанию самого автора, стали так называемые числа Фибоначчи – последовательность чисел, открытая Фибоначчи в XIII веке. Числа Фибоначчи и связанное с ними золотое сечение играют важную роль в структуре развития форм и процессов в природе, в том числе в развитии по спирали [9].
Всего Эллиот обнаружил 13 волн, постоянно возникающих в данных о рыночных ценах. Эллиотт назвал, определил и проиллюстрировал эти волны. Описал, как, связанные между собой, они формируют более крупные по размеру аналоги, которые, в свою очередь, формируют те же самые модели ещё большего размера и т. д. Эллиотт назвал это явление волновым принципом.
Многие критики использования модели Элиота для прогноза считают, что на основе волнового принципа невозможно единообразно определить где волны начинаются и заканчиваются, и поэтому прогнозы на основе Эллиотта склонны носить субъективные поправки. Тем не менее, модель Элиота применяется в практике принятия решений инвесторами фондовых рынках и рассматривается как инструмент технического анализа.
Волны Элиота являются фракталами или самоподобными регулярными структурами. В современной науке фрактальность поведения сложных нелинейных систем считается строго доказанным математическим фактом [10].
В применении к фондовому рынку Доу предложил свою теорию, основанную на циклах [11]. В его теории важное значение отводится информационным сигналам и уровням информационного шума, позволяющим инвесторам принять то или иное решение.
Экономические циклы присущи развитию и экономических систем. Под экономическими циклами понимаются колебания экономической активности, состоящие в повторяющемся сжатии и расширении экономики (экономического спада и подъема). Циклы носят периодический, но, обычно нерегулярный характер. Обычно (в рамках неоклассического синтеза) интерпретируются как колебания вокруг долгосрочного тренда развития экономики [12].
Детерминистская точка зрения на причины экономических циклов исходит из предсказуемых, вполне определенных факторов; роста производительных сил, вовлечения в оборот всё большего количества природных ресурсов и т.д Стохастическая точка зрения исходит из того, что циклы порождаются факторами случайной природы и представляют собой реакцию экономической системы на внутренние и внешние импульсы.
Обычно выделяют четыре основных вида экономических циклов:
• длинные волны Кондратьева (характерный период – 50-60 лет).
• ритмы Кузнеца (характерный период – 15–20 лет);
• Циклы Чижевского (характерный период – 11–16 лет, привязан к периоду солнечной активности);
• среднесрочные циклы Жюгляра (характерный период – 6-13 лет);
• краткосрочные циклы Китчина (характерный период – 2-3 года);
Концепция Кондратьева активно исследуется и развивается на протяжении всего времени существования, однако широкого консенсуса в сообществе учёных-экономистов на счёт её практической применимости не достигнуто. [13]. На рис. 4 представлена динамика изменений в мировой экономике в соответствии с концепцией Кондратьева, обусловленных сменой базовых отраслей на основе технологических революций.
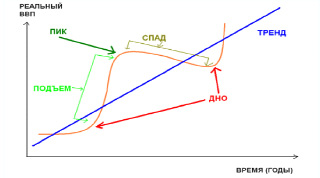
Рис. 3. Колебания вокруг долгосрочного тренда развития экономики [12]
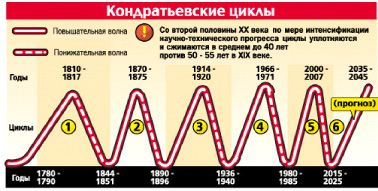
Рис. 4. Циклы Кондратьева в мировой экономике [13]
Инфраструктурные инвестиционные циклы (15-25 лет) изучил нобелевский лауреат Саймон Кузнец [14]. Циклы (ритмы) Кузнеца имеют продолжительность примерно 15-25 лет. Были открыты им в 1930 году. Кузнец связывал эти волны с демографическими процессами, в частности, притоком иммигрантов и строительными изменениями, поэтому он назвал их «демографическими» или «строительными» циклами.
В настоящее время рядом авторов ритмы Кузнеца рассматриваются в качестве технологических, инфраструктурных циклов. В рамках этих циклов происходит массовое обновление основных технологий. Кроме того, хорошо совпадают с циклом Кузнеца большие циклы цен на недвижимость на примере Японии 1980–2000 гг. и длительность большой полуволны подъема цен в США.
Высказывалось также и предложение рассматривать ритмы Кузнеца в качестве третьей гармоники Кондратьевской волны. Четкой периодичности не наблюдается, поэтому исследователи берут среднее значение в 15-20 лет.
Самым оригинальным, заветным направлением работ А.Л. Чижевского стала его теория гелиотараксии [15]. Ее основной закон он сформулировал в 1922 г. в следующей интерпретации: «состояние предрасположения к поведению человеческих масс есть функция энергетической деятельности Солнца». В наше время также признано, что активность солнца напрямую влияет на многие сферы человеческой деятельности, работоспособность и здоровье самого человека, природные явления и т.д.
Циклы Жюгляра – среднесрочные экономические циклы с характерным периодом в 7-11 лет [16]. Названы по имени французского экономиста Клемана Жугляра, одним из первых описавшего эти циклы. В рамках циклов Жугляра наблюдаются колебания не просто в уровне загрузки существующих производственных мощностей (и, соответственно, в объеме товарных запасов), но и колебания в объемах инвестиций в основной капитал Дополнительная задержка формируется и между спадом спроса и ликвидацией соответствующих производственных мощностей. Циклические экономические кризисы/рецессии могут рассматриваться в качестве одной из фаз цикла Жугляра (наряду с фазами оживления, подъема и депрессии). Вместе с тем от фазы кондратьевской волны зависит глубина этих кризисов.
Циклы Китчина – краткосрочные экономические циклы с характерным периодом 3-4 года, открытые в 1920-е годы английским экономистом Джозефом Китчином [16]. Сам Китчин объяснял существование краткосрочных циклов колебаниями мировых запасов золота, однако в наше время такое объяснение не может считаться удовлетворительным. В современной экономической теории механизм генерирования этих циклов обычно связывают с запаздываниями по времени (временными лагами) в движении информации, влияющими на принятие решений коммерческими фирмами.
В отличие от циклов Китчина в рамках циклов Жюгляра мы наблюдаем колебания не просто в уровне загрузки существующих производственных мощностей (и, соответственно, в объеме товарных запасов), но и колебания в объемах инвестиций в основной капитал.
Наложение циклов друг на друга в определённом историческом интервале может привести к глобальному экономическому кризису (рис. 5).
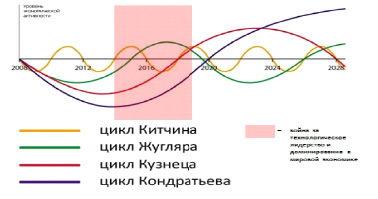
Рис. 5. Кризис экономической системы как сочетание циклических процессов [16]
Характерной особенностью циклического развития является то, что это, в первую очередь, развитие, а не колебания вокруг некой постоянной (потенциальной) величины. Цикличность означает развитие по спирали, а не по замкнутому кругу. Этот механизм прогрессивного движения в самых разных его формах. В экономической литературе особо подчеркивается, что циклические колебания происходят около траектории долгосрочного роста (векового тренда).
Теория реальных экономических циклов объясняет спады и подъемы воздействием реальных факторов. В индустриальных странах этим может быть появление новых технологий, изменение цен на сырье. В аграрных странах – урожай или неурожай. Также толчком к переменам могут стать форс-мажорные ситуации (война, революция, стихийные бедствия). Предвидя изменение экономической обстановки в лучшую или худшую сторону, домохозяйства и фирмы массово начинают экономить или больше тратить. В результате сокращается или возрастает совокупный спрос, уменьшается или увеличивается оборот розничной торговли. Фирмы получают меньше или больше заказов на изготовление продукции, соответственно меняется объем производства, занятость. Меняется деловая активность: фирмы начинают сокращать ассортимент выпускаемой продукции или наоборот запускают новые проекты, берут кредиты на их осуществление. То есть вся экономика колеблется, стремясь прийти в равновесие.
Для выявления волновых свойств экономических процессов и использования полученных данных в модели с целью определения момента времени принятия решений необходимо провести гармонический анализ динамики изменения ключевого экономического показателя (КЭП) во времени. Отдельные гармоники КЭП могут соответствовать вполне конкретным экономическим или социальным причинам.
В тоже время, наряду с детерминистскими процессами, которые носят циклический характер, большую, а иногда и определяющую роль играют и случайные события, которые могут влиять в том числе и на параметры этих циклических процессов.
Эти события можно условно подразделить на два класса. К первому классу относятся события, которые в принципе невозможно предсказать. К таким событиям, относятся, например, ядерная катастрофа в Чернобыле или падение пассажирского аэробуса в Альпах в 2015 г.
Ко второму классу событий, которые заранее можно предсказать с некоторой вероятностью, относятся, например, кризис 2008 г. или урегулирования иранской ядерной проблемы. События как первого, так и второго класса влияют на экономическую систему, но вторые действуют постоянно и в течение интервального прогноза играют наиболее существенную роль. Эти события могут быть взаимосвязаны и порождают информационные сигналы, которые в свою очередь влияют на ключевые экономические показатели (экономические агенты), которые также образуют сеть. Так как информационные сигналы о событиях в первую очередь влияют на финансовые показатели и потоки в глобальной экономике, которые взаимосвязаны, то последние также можно представить в виде сети финансовых агентов. Общая модель экономической системы, таким образом, может быть представлена в виде взаимосвязанной системы из трёх сетей: сети ключевых показателей экономической системы (экономических агентов), сети финансовых потоков (финансовых агентов) и сети информационных сигналов (информационных агентов), рис. 6.
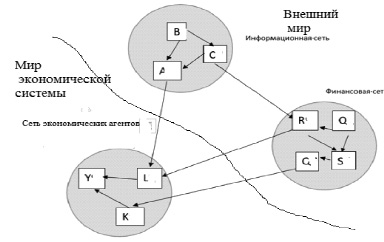
Рис. 6. Пример взаимосвязи информационных, финансовых и экономических агентов в тройственной сети: Y, K, L и другие – экономические переменные (экономические агенты); S, R, Q, L и другие – переменные, характеризующие финансовые потоки (финансовые агенты); A, B, C и другие – информационные сигналы о появлении вероятных событий (информационные агенты)
Представленная модель характерна для хроноэкономике. В отличие от традиционных моделей временного ряда в ней учитываются следующие концептуальные предпосылки.
Ключевые экономические показатели (КЭП) экономической системы рассматриваются как экономические агенты, характеристики которых имеют волновые свойства и подвержены стохастическим изменениям.
КЭП являются вершинами сети, на которые воздействуют внешние информационные и финансовые агенты.
Информационные и финансовые сети также обладают волновыми свойствами, а их агенты также подвержены стохастическим изменениям.
Агенты информационной и финансовой сетей можно рассматривать как взаимосвязанные случайные события. В виртуальной области, в которую мы включаем существенные случайные события, влияющие на интересующие насКЭП, существуют упорядоченные структуры взаимосвязанных событий и вероятность появления отдельного события можно представить в виде некоторого графа, что и сделал Томас Байес.
Байесовская сеть (или Байесова сеть, Байесовская сеть доверия) – это графическая вероятностная модель, представляющая собой множество переменных и их вероятностных зависимостей [17]. Например, байесовская сеть может быть использована для вычисления вероятности того, чем болен пациент по наличию или отсутствию ряда симптомов, основываясь на данных о зависимости между симптомами и болезнями. Математический аппарат Байесовых сетей создан американским ученым Джуда Перлом, лауреатом Премии Тьюринга (2011).
Формально, байесовская сеть – это направленный ациклический граф, каждой вершине которого соответствует случайная переменная, а дуги графа кодируют отношения условной независимости между этими переменными.
Вершины могут представлять переменные любых типов, быть взвешенными параметрами, скрытыми переменными или гипотезами. Существуют эффективные методы, которые используются для вычислений и обучения байесовских сетей.
Формула совместного распределения вероятностей в узлах сети записывается как результат локальных распределений в узле и его предках:
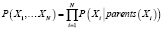 .
.
Байесовские сети доверия позволяют решать две важные задачи: прогноз и диагноз. Существует множество алгоритмов, представляющих приблизительный вероятностный вывод: на основе посылки сообщений, преобразовании Байесовской сети в дерево, стохастических выборок: вероятностного взвешивания, выборки по собственной важности, выборки по адаптивной важности, случайной выборки и др. Некоторые из этих алгоритмов реализованы в приложениях с открытым кодом.
Если исходить из фундаментальной гипотезы о волновых свойствах любых процессов в природе, то и вероятности в виртуальной области событий представляют собой некие «волны вероятности» и событие реализуется когда эти волны образуют некий резонанс. Такого рода модель ещё предстоит разработать, но в качестве уже оправдавшего себя подхода для определения вероятностей взаимосвязанных событий можно использовать и сеть доверия Байеса.
Сложность применения сетей доверия к исследованию реальных экономических и социальных процессов заключается в громоздкости вычислений при больших размерах сетей и в приблизительности оценок вероятности появления событий, влияющих на интересующие нас процесс или событие. Задачу можно попытаться облегчить, если рассматривать случайные события как бинарные переменные и определять их значение на основе бинарной модели выбора [18].
Модель бинарного выбора – применяемая в эконометрике модель зависимости бинарной переменной (принимающей всего два значения – 0 и 1) от совокупности факторов.
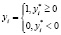 .
.
Построение обычной линейной регрессии для таких переменных теоретически некорректно, так как условное математическое ожидание таких переменных равно вероятности того, что зависимая переменная примет значение 1, а линейная регрессия допускает и отрицательные значения и значения выше 1 . Поэтому обычно используются некоторые интегральные функции распределения. Чаще всего используются нормальное распределение (пробит), логистическое распределение (логит) , распределение Гомперца (гомпит). В логистическом распределении вероятность события определяется функцией
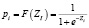 ,
,
где Z является линейной функцией объясняющих переменных:
Z = b0 + b1xi1 + ... + bjxij + ... + bkxik + ei.
Переменная Z является внутренней, объясняемой переменной, а Xi – внешние, объясняющие переменные.
Комбинированный подход на основе сетей доверия и бинарных моделей расширяет возможности первого и второго методов и имеет большую объяснительную способность, чем каждый из них в отдельности. Их использование наиболее целесообразно в агент-ориентированных моделях сложных экономических систем. Агент-ориентированные модели (АОМ) – специальный класс вычислимых моделей, основанных на индивидуальном поведении множества агентов, и создаваемых для компьютерных симуляций. Эти компьютерные симуляции тесно взаимосвязаны со следующими понятиями: вычислимая экономика, сложные системы, метод Монте-Карло, вычислительная социология, системы с множеством агентов и эволюционное программирование. Агент-ориентированные модели, на наш взгляд, должны дополняться и интегрироваться с моделями, в которых отражены фундаментальные свойства изучаемых больших систем.
В модели экономической системы на основе представленной тройственной сети таким фундаментальным свойствам происходящих в ней процессах является их колебательный или волновой характер. Колебательные процессы в подсистемах тройственной сети представляют собой комбинации гармоник, определяемых свойствами элементов этих подсистем.
Можно провести аналогию между моделью экономической системы в виде тройственной сети и организмом человека. Организм человека также можно представить в виде тройственной сетевой модели состоящей из информационной сети (мозг и нервная сеть), кровеносной системы (аналог финансовой сети) и сеть органов (сердце, печень, желудок и др.) – аналог сети производителей и потребителей товаров и услуг (экономических агентов). И в нервной системе, и в кровеносной, и в каждом органе происходят волновые процессы, давно известные, измеряемые и изучаемые в медицине. Наличие в живой и неживой природе, а также в социально-экономической сфере, созданной человеком, волновых и колебательных процессов является их фундаментальным и общим свойством. Например, в организме человека обнаружены биологические ритмы – (биоритмы) периодически повторяющиеся изменения характера и интенсивности биологических процессов и явлений [19]. Биоритмы свойственны живой материи на всех уровнях ее организации – от молекулярных и субклеточных до биосферы, и являются фундаментальным процессом в живой природе. Одни биологические ритмы относительно самостоятельны, например, частота сокращений сердца, дыхания. Другие связаны с приспособлением организмов к геофизическим циклам – суточным, например, колебания интенсивности деления клеток, обмена веществ, двигательной активности животных. Имеются приливные, например, открывание и закрывание раковин у морских моллюсков, связанные с уровнем морских приливов, а также годичные, как например, изменение численности и активности животных, роста и развития растений и др. [12].
Колебательные и волновые свойства систем в живой и неживой природе изучаются давно. Особое внимание привлекает такое явление как резонанс. Слово «резонанс» (от лат. Resono – откликаюсь) в самом общем смысле означает сильный отклик какой-либо системы на небольшое внешнее воздействие. Важно то, что такой сильный отклик – избирателен, то есть он возникает только при определенных параметрах внешнего воздействия.
Резонанс возникает, если частота внешнего воздействия сравнивается с собственной частотой колебаний системы. Было бы странно, если бы резонансные явления не присутствовали в социально-экономических системах.
Рассматривая модель экономической системы на основе тройственной сети мы предполагаем, что решающую роль в явлении резонанса играет сеть информационных сигналов и потоков. В этой сети «информационный шум» препятствует слабым информационным сигналам вызвать сильный отклик, который приводит к заметным или очень значимым экономическим событиям, например, кризису. Однако в науке известно, что в системе происходит усиление периодического сигнала под действием шума определенной мощности. Это явление называется стохастическим резонансом [20]. Он является универсальным явлением, присущим нелинейным системам (природным и искусственным), находящимся одновременно под хаотическим и слабым периодическим воздействием. Информационные сигналы в тройственной сети не влияют на её существенные характеристики (потоки товаров и финансов) до тех пор, пока не создадутся условия для стохастического резонанса вследствие возрастания уровня информационного шума. Наличие периодических составляющих и шума позволяют, используя слабые сигналы внешнего информационного воздействия, вызывать существенные изменения (стохастический резонанс) ключевых показателей экономической системы как с положительным, так и отрицательным знаком.
Явление стохастического резонанса в экономической системе также должно быть отнесено к области изучения в хроноэкономике.
В заключение можно сформулировать следующие выводы относительно цели и основных задач хроноэкономики .
Цель хроноэкономики – исследование влияния фактора времени на экономические процессы.
Определена основная задача хроноэкономики как выбор времени для принятия управленческого решения (действия) с целью наилучшего изменения ключевых параметров экономической системы с наименьшими затратами.
Предложена обобщённая модель в рамках хроноэкономики для управления экономической системой на основе тройственной сети экономических, финансовых и информационных агентов.
Поставлена задача анализа волновых и стохастических свойств экономических, финансовых и информационных агентов для эффективного управления ключевыми показателями экономической системы.
Поставлена задача использования явления стохастического резонанса в экономических система в целях эффективного управления её ключевыми экономическими показателями

