В [1, 2, 3] предложена экономико-математическая модель долевого распределения поступлений от уплаты конкретного вида налога в виде абстрактного адаптивного устройства, способного хорошо приспосабливаться к условиям изменения внешней среды – модель стохастического автомата A, функционирующего в стационарной случайной среде. В реальной ситуации бюджетного регулирования в процессе долевого распределения участвуют поступления от некоторого подмножества налогов. Для решения такой задачи авторами статьи предложена математическая модель поведения описанного в [4,5] автомата A в переключаемых случайных средах. При этом для каждого вида налога Nx предлагается рассматривать свою отдельную случайную среду, вероятностные характеристики которой описываются вектором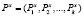 
, где 
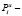оценка вероятности выигрыша автомата A в состоянии с номером i при воздействии случайной среды, формируемой поступлениями от уплаты налога Nx, 
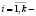номера состояний автомата A. Выигрыш автомата понимается в смысле, описанном в [1]. Допустим, что в процессе долевого распределения доходов в порядке бюджетного регулирования участвуют n видов налогов: 
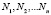. Тогда имеем систему векторов 
, 
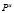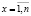, описывающих вероятностные характеристики случайных сред 
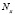, в которые погружается автомат A [6,7]: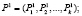 
…
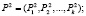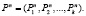
Переход к составной случайной среде приводит к следующим изменениям поведения автомата A. Кроме переходов из одного состояния в другое, автомат A может осуществлять переходы из одной случайной среды в другую.
Автомат A находится в переключаемой случайной среде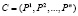 
, если в каждый момент времени 
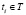он функционирует в одной из случайных сред 
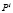множества 
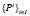, где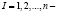 
множество индексов. Обозначим через 
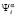такое состояние системы «автомат – переключаемая среда», при котором автомат A находился в состоянии 
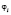, а переключаемая среда – в состоянии Pa. В качестве выходного воздействия системы «автомат – переключаемая среда» на внешнюю среду в момент времени 
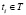в состоянии 
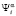примем величину 
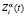, смысл которой совпадает со смыслом выходного воздействия автомата A в однородной случайной среде [1]. Следовательно, выход системы 
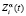интерпретируется как величина текущего запаса бюджета в условиях таких отчислений от уплаты налога вида 
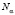, доля которых составляет 
.
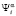При этом если в момент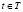 
система находится в состоянии 
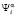и произвела действие 
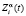, то в момент времени 
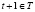это действие повлечёт за собой поступление входного сигнала 
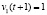(т.е. «выигрыш») с вероятностью 
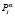и поступление входного сигнала 
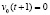(т.е. «проигрыш» или «штраф») с вероятностью 
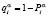. Если автомат A в момент времени 
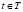находился в случайной среде 
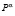, то в момент 
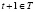он осуществит переход в случайную среду 
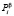с вероятностью 
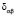. Оценка вероятности 
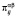перехода системы «автомат – переключаемая среда» из состояния 
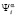в состояние 
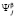определяется следующим образом: 
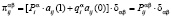, где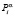 
, 
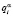– соответственно оценки вероятностей выигрышей и проигрышей системы «автомат – переключаемая среда» в состоянии 
; 
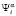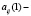оценка вероятности перехода автомата A из состояния 
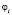в состояние 
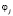при поступлении входного сигнала 
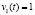, т.е. при «выигрыше»; 
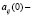оценка вероятности перехода автомата A из состояния 
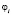в состояние 
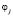при поступлении входного сигнала 
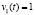, т.е. при «проигрыше» (или «штрафе»); 
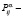вероятность перехода автомата A из состояния 
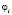в состояние 
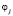при любом входном сигнале.
Следовательно, вероятностные характеристик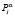и 
и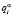 
, 
, 
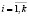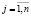представляют собой оценки вероятностей соответственно дефицита и профицита, к которым приведёт пребывание системы «автомат – переключаемая среда» в состоянии 
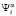, интерпретируемом как доля отчислений денежных средств в бюджет нижестоящего уровня бюджетной системы РФ от уплаты налога вида 
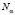в порядке бюджетного регулирования. Матрица перехода 
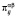системы «автомат – переключаемая среда», когда автомат A переходит из состояния с номером i в состояние с номером j при переключении случайной среды, в которую погружён автомат, из состояния с номером a в состояние с номером b, имеет следующий вид [8]:
.
Финальные вероятности R системы «автомат-составная среда» представляют собой вектор
,
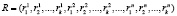где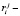 
финальная вероятность пребывания автомата в состоянии 
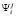, т.е. когда автомат находится в состоянии с номером i, а вероятностная среда – в состоянии с номером j. Для матрицы 
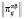, элементы которой определяются выражениями, приведёнными в таблице 1, системы уравнений для определения финальных вероятностей 
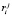структуры «автомат-переключаемая среда» запишутся в следующем виде.
Системы уравнений для определения финальных вероятностей при состоянии случайной среды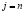 
.
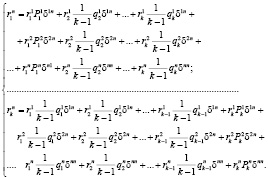
Примем, что составная вероятностная среда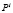 
, 
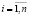переключается из одного состояния 
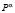в другое состояние 
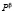с одинаковой вероятностью 
, 
, 
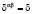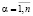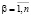. Тогда на основе полученных уравнений для финальных вероятностей можно сделать вывод, что в условиях принятых допущений имеют место равенства:
; 
, …, 
.
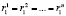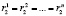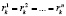Обозначим эти вероятности переменными соответственно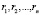 
. Решение составленных систем уравнений с учётом условия нормировки 
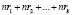позволило получить следующие выражения для финальных вероятностей пребывания системы «автомат–переключаемая среда» в своих состояниях [9]:
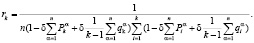
Финальные вероятности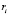 
, 
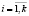зависят от вероятностей выигрышей 
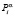и проигрышей 
, 
, 
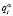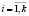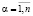в каждом состоянии автомата, вычисление которых предполагается осуществлять на базе функционирования имитационной модели, воспроизводящей изменение величины остатков денежных средств в бюджете при случайном характере вариаций доходов и расходов.