О численном методе, алгоритме и комплексе программ
Некоторые исследования в области моделирования нестационарных волн напряжений в деформируемых областях различной формы рассмотрены в следующих работах [1–10].
Рассматривается моделирование нестационарных волн напряжений в деформируемых областях с помощью метода конечных элементов в перемещениях. Задачи решаются методом сквозного счета, без выделения разрывов. То есть применяется однородный алгоритм. За основные неизвестные в узле конечного элемента приняты два упругих перемещения и две скорости упругих перемещений. Основные соотношения метода конечных элементов в перемещениях по пространственным координатам получены с помощью принципа возможных перемещений, то есть с помощью метода динамического равновесия внутренних и внешних сил.
Для аппроксимации по пространственным координатам применяются треугольные конечные элементы с линейной аппроксимацией упругих перемещений и прямоугольные конечные элементы с четырьмя узловыми очками с билинейной аппроксимацией упругих перемещений. Для аппроксимации по временной координате применяются линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией перемещений. С помощью метода конечных элементов в перемещениях линейная задача с начальными и граничными условиями приведена к линейной задаче Коши. С помощью конечноэлемнтного варианта метода Галеркина система обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями приведена к явной двухслойной конечноэлементной линейной схеме в перемещениях для внутренних и граничных узловых точек.
На основе метода конечных элементов в перемещениях разработаны численный метод, алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать задачи при нестационарных динамических воздействиях на сложные деформируемые системы.
Моделирование плоской продольной упругой волны в полуплоскости
Некоторая информация о физической достоверности результатов разработанного численного метода, алгоритма и комплекса программ рассмотрена в следующих работах [4–7, 9].
Рассмотрим задачу о воздействии плоской продольной волны в виде импульсного воздействия (восходящая часть – четверть круга, средняя – горизонтальная, нисходящая – линейная) (рис. 2) на упругую полуплоскость (рис. 1). На границе полуплоскости AB приложено нормальное напряжение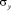 
, которое при 
(
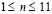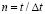) изменяется от 0 до P, при 
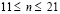равно P и при 
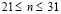изменяется от P до 0 (
, 
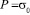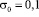МПа). Граничные условия для контура BCDA при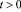 
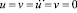. Отраженные волны от контура BCDA не доходят до исследуемых точек при 
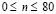. Расчеты проведены при следующих исходных данных: 
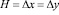; ∆t = 1,393⋅10-6 с; E = 3,15⋅104 МПа (3,15⋅105 кгс/см2); n= 0,2; r=0,255⋅104 кг/м3 (0,255⋅10-5 кгс с2/см4); Cp= 3587 м/с; Cs= 2269 м/с. Исследуемая расчетная область имеет 20402 узловых точек. Решается система уравнений из 81608 неизвестных.
На рис. 3–5 представлено изменение нормального напряжения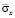 
(
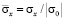) во времени n в точках B1–B3.
На рис. 6–8 представлено изменение нормального напряжения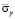 
(
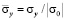) во времени n в точках B1–B3.
В данном случае можно использовать условия на фронте плоской волны, которые изложены в работе [1].
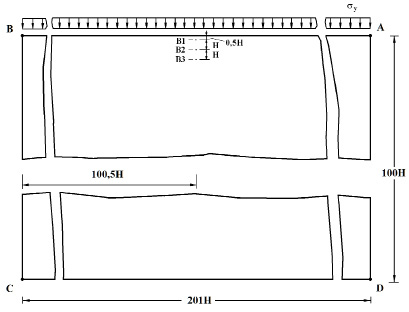
Рис. 1. Постановка задачи о распространении плоских продольных волн в упругой полуплоскости
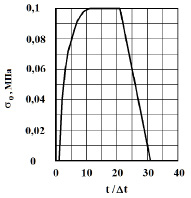
Рис. 2. Импульсное воздействие (восходящая часть – четверть круга, средняя – горизонтальная, нисходящая – линейная)
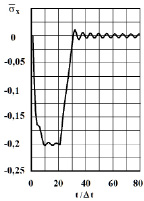
Рис. 3. Изменение нормального напряжения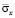 
во времени 
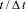в точке B1
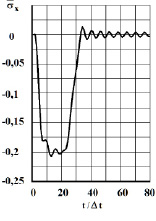
Рис. 4. Изменение нормального напряжения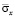 
во времени 
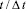в точке B2
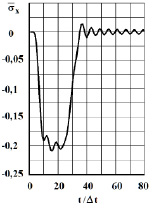
Рис. 5. Изменение нормального напряжения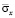 
во времени 
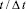в точке B3
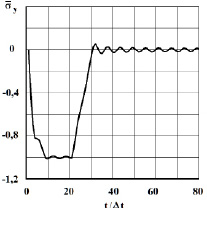
Рис. 6. Изменение нормального напряжения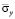 
во времени 
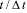в точке B1
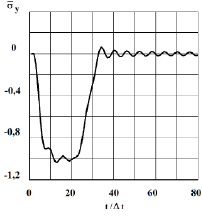
Рис. 7. Изменение нормального напряжения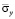 
во времени 
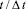в точке B2
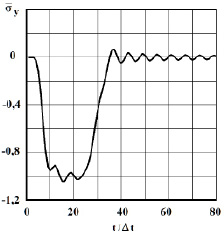
Рис. 8. Изменение нормального напряжения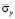 
во времени 
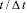в точке B3
Предположим, что от некоторых точек упругой среды производится какое-то возмущение. Тогда из этих точек во все стороны начинают излучаться волны. На некотором расстоянии от центра возмущения рассматриваемые волны можно представить как плоские. Тогда все частицы движутся параллельно направлению распространения волны. Такие волны принято считать плоскими. На фронте плоской продольной волны имеются следующие аналитические зависимости для плоского напряженного состояния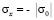 
и 
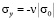. Отсюда видим, что точное решение задачи соответствует воздействию 
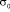(рис. 2).
Для упругих нормальных напряжени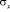й 
и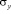 
имеется хорошее качественное и количественное согласование с результатами точного решения. Таким образом, можно сделать вывод, что на точность численного решения оказывает влияние аппроксимация воздействия.
Сравнение результатов нормальных напряжений, полученных с помощью метода конечных элементов в перемещениях, при решении задачи о распространении плоских продольных волн в виде импульсного воздействия (восходящая часть – четверть круга, средняя – горизонтальная, нисходящая – линейная) в упругой полуплоскости с результатами аналитического решения, показало хорошее совпадение. На основании проведенных исследований можно сделать вывод о физической достоверности результатов численного решения задач о распространении импульсных воздействий в деформируемых телах.