В статье рассмотрены основы исследования прибортового массива, сложенного пластичными породами. В процессе горных работ происходит изменение параметров откоса (высоты, угла наклона и конфигурации), что приводит к изменению напряженно-деформированного состояния прибортового массива. При неизменных конструктивных параметрах борта происходят изменения поля напряжений и деформаций во времени, которые начинают отсчет с момента времени t0 начала формирования откоса. В результате изменения напряженно-деформированного состояния в прибортовом массиве возникают предельные (пластические) зоны в соответствии с теорией предельного равновесия. Несущая способность этих участков достигает своего предела и дальнейший рост напряжений там невозможен, происходит перераспределение напряжений на окружающий массив и рост пластической области.
Нарушение устойчивого состояния прибортового массива связано с возникновением и развитием областей пластического (предельного) состояния горных пород и формированием в них поверхностей скольжения.
В процессе горных работ происходит изменение параметров откоса (высоты, угла наклона и конфигурации), что приводит к изменению напряженно-деформированного состояния прибортового массива. При неизменных конструктивных параметрах борта происходят изменения поля напряжений и деформаций во времени, которые начинают отсчет с момента времени t0 начала формирования откоса. В результате изменения напряженно-деформированного состояния в прибортовом массиве возникают предельные (пластические) зоны в соответствии с теорией предельного равновесия. Несущая способность этих участков достигает своего предела и дальнейший рост напряжений там невозможен, происходит перераспределение напряжений на окружающий массив и рост пластической области. Достижение откосом предельного состояния означает формирование сплошной пластической области, отделяющей откос от прибортового массива, в которой формируются поверхности скольжения. При решении плоской задачи теории предельного равновесия в исследуемой области формируется два семейства линий скольжения (в соответствии с парностью касательных напряжений), которые представляют собой след поверхности скольжения в исследуемой плоскости. Линии скольжения в каждой своей точке касаются площадки максимального касательного напряжения и могут быть описаны параметрическими уравнениями
x = x (α;β); y = y (α;β), (1)
где α;β – параметры линии скольжения.
При использовании теории предельного равновесия в качестве гипотезы прочности, отклонение линий скольжения от первого главного напряжения составит угол ±(45° – ρ/2).
Обозначим θ угол наклона касательной к линии первого семейства, отсчитываемый в положительном направлении от оси X. Тогда дифференциальные уравнения линий 1-го семейства (α-линии) и 2-го семейства (β-линии) соответственно будут иметь вид
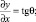
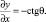 (2)
(2)
Рассмотрим откос высотой Н и углом откоса α, находящийся в предельном состоянии. Построим предполагаемую круглоцилинд-рическую поверхность скольжения, для чего определяем ширину призмы возможного обрушения по формуле [1]
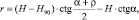 (3)
(3)
где 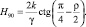
Разбиваем призму возможного обрушения и поверхность откоса на N равных частей и строим N поверхностей скольжения. Построенное семейство дуг окружностей приближенно совпадает с линиями скольжения 1-го рода. При построении линий скольжения 2-го рода учитывается то обстоятельство, что линии скольжения 1-го и 2-го рода пересекаются под углом (90° – r). Такое разбиение призмы возможного обрушения на блоки отвечает физической сущности деформирования приоткосного массива [1]. С глубины Н90 массив достигает предельного (пластического) состояния, которое, очевидно, распространяется на область СДЕ и полосу малой ширины, заключающую линию скольжения АЕ. Уравнение предельного равновесия Кулона является, по сути, уравнением физической модели жестко-пластического тела с элементом трения. В прямоугольной системе координат XYZ, где ось Z перпендикулярна плоскости сечения, а sz является одним из главных напряжений, имеем
σz – σ = 0; σ = 0,5 (σx + σy). (4)
Остальные главные напряжения являются корнями квадратного уравнения
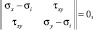 (5)
(5)
откуда
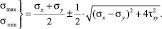 (6)
(6)
Таким образом, главные напряжения равны
σ1 = σ + τ; σ2 = σ; σ3 = σ – τ, (7)
где максимальное касательное напряжение
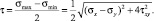 (8)
(8)
Напряженное состояние в каждой точке массива характеризуется наложением гидростатического напряженного состояния на напряжения чистого сдвига [1]. При достижении пластического состояния должно выполняться условие текучести
τ = τs = const, или σmax – σmin = 2 τs. (9)
В соответствии с теорией предельного равновесия
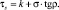
Из формулы (8) получим
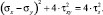 (10)
(10)
Добавим к этому условию два дифференциальных уравнения равновесия с учетом объемных (гравитационных) сил
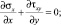
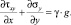 (11)
(11)
Если на границе рассматриваемой области заданы напряжения, то имеем полную систему уравнений равновесия для определения напряженного состояния в состоянии текучести
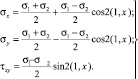 (12)
(12)
Обозначим полусумму главных напряжений через σ, а полуразность – через ε и перейдем к углу θ = [(1, x) – π/4]. Тогда
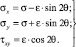 (13)
(13)
При этом условие текучести выполняется. Подставляя полученные значения в уравнения равновесия (11), получаем систему двух нелинейных дифференциальных уравнений в частных производных первого порядка относительно неизвестных функций σ(x, y) и θ(x, y)
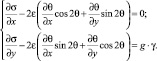 (14)
(14)
Данная система уравнений является системой гиперболического типа, которая имеет два различных вещественных семейства характеристических линий, совпадающих с линиями скольжения.
Для произвольной точки линии скольжения справедливы соотношения Г. Генки [3]
– для семейства линий a
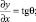
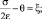 (15)
(15)
– для семейства линий b
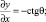
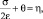 (16)
(16)
где x и h – постоянные величины.
При переходе от одной линии скольжения семейства α к другой параметр ξ изменяется. Аналогично, при переходе от одной линии семейства β к другой изменяется параметр η. Таким образом, ξ зависит только от параметра β, а η – только от α, т.е.
ξ = ξ(β); η = (α).
Если определено поле линий скольжения и на них значения параметров ξ и η, то в каждой точке известны σ и θ, т.е. известны компоненты напряжений.
Система дифференциальных уравнений равновесия (14) может быть линеаризована. За неизвестные функции удобно принять параметры ξ и η. Выполним замену
σ = ε(ξ + η);
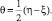
Умножая затем второе из полученных уравнений последовательно на tgθ и (–ctgθ) и складывая с первым, получаем
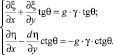 (17)
(17)
Получаем линейную неоднородную систему дифференциальных уравнений с переменными коэффициентами.
Построение аналитических решений для линеаризованных уравнений (17) связано с большим объемом вычислений. Более простыми и доступными являются приближенные методы построения полей скольжения, основанные на переходе к конечно-разностным соотношениям и использовании свойств линий скольжения [1]. Множество плоских задач теории пластичности можно представить как комбинацию трёх основных элементарных задач – задачи о начальных (граничных) значениях (задача Коши), начальная характеристическая задача (задача Римана) и смешанная задача [1]. Таким образом, при исследовании напряженного состояния прибортового массива необходимо решать задачу Коши для области CDE (рисунок 1), имеющую прямолинейную свободную границу CD, равномерно загруженную давлением р = – γН90. Вдоль границы CD имеем равномерное напряженное состояние
σу = –γН90;
σх = ±2ε – γН90;
τху = 0;
θ = π/2 – μ = π/4 + ρ/2.
При построении решений в области, расположенной ниже призмы активного давления, принимаем в качестве семейства a-линий скольжения семейство дуг окружностей, образующих угол m = π/4 – ρ/2 с поверхностью откоса у нижней бровки и вертикалью на сопряжении с призмой CDE. Таким образом, величина угла θ изменяется от (π/4 + ρ/2) на границе с призмой до (α – μ) на поверхности откоса. Угол θ в любой точке А дуги скольжения может быть определен по формуле
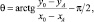 (18)
(18)
где х0, у0 – координаты центра окружности; хА, уА – координаты точки А дуги скольжения.
Если ввести естественную прямоугольную систему координат S1AS2, связанную с a-линиями скольжения и повернутую относительно системы координат ХОУ на угол θ, то дифференциальные уравнения равновесия (14) примут вид
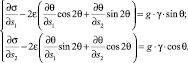 (19)
(19)
Уравнения равновесия (19) справедливы для произвольной системы координат S1AS2. Если координатная ось AS1 совпадает с направлением касательной к α-линии скольжения, то уравнения принимают более простую форму
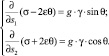 (20)
(20)
Соотношения Генки для плоской задачи в области прибортового массива, где удовлетворяются условия пластичности и предельного равновесия вдоль линий скольжения α и β, примут вид:
– для α-линий
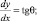
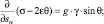 (21)
(21)
– для b-линий
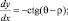
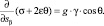 (22)
(22)
В пределах элементарного блока расчетной сетки принимаем θ = const, тогда дифференциальные уравнения можно заменить уравнениями в приращениях
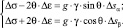 (23)
(23)
Складывая оба уравнения, получим
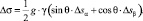 (24)
(24)
Вычитая из второго уравнения системы первое, получим
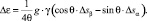 (25)
(25)
Сгущаем расчетную сетку в пределах каждого элементарного блока и вычисляем значения θ в узлах сетки по формуле (17). Переходим от дифференциальных соотношений (20) и (21) к конечно-разностным, последовательно определяя значения σ в узлах сетки. При рассмотрении напряженного состояния массива, расположенного ниже призмы активного давления, для каждого четырехугольного расчетного блока необходимо решать начальную характеристическую задачу, а для последнего треугольного блока каждого слоя – смешанную задачу со свободной границей, лежащей на поверхности откоса.

