В настоящее время обучение во всех вузах России осуществляется в соответствии с Федеральными государственными образовательными стандартами высшего профессионального образования третьего поколения (ФГОС ВПО). Методологической основой образовательного стандарта в государственных документах признан компетентностный подход к обучению. Основным результатом обучения является определенный набор компетенций – совокупности смысловых ориентаций, знаний, умений, опыта деятельности учащегося [5].
В ФГОС ВПО (V раздел) в качестве требований к результатам освоения бакалаврами основных образовательных программ выделено два основных блока компетенций: общекультурные, обязательные для всех профилей, и профессиональные, отражающие специфику определенной профессиональной деятельности. В учебных программах, составленных на основе ФГОС ВПО, в качестве требований к результатам освоения конкретных дисциплин выделяются также предметные компетенции, включающие предметные знания, умения, навыки, способы мышления.
Под математической компетенцией (на основе определений, предложенных А.В. Хуторским и разделяющимися большей частью педагогического сообщества [5]) будем понимать совокупность взаимосвязанных качеств личности, включающих математические знания, умения, навыки, способы мышления и деятельности, а также способность приобретать новые математические знания и использовать их в дальнейшей профессиональной деятельности. Математическая компетентность есть результат освоения математической компетенции, ее практическая реализация.
Формируя список математических компетенций бакалавров технических вузов, мы обратились к сборнику примерных программ математических дисциплин ФГОС ВПО третьего поколения, разработанных Научно-методическим советом по математике Министерства образования и науки РФ под руководством Л.Д. Кудрявцева [3]. В пояснительной записке к сборнику указано, что в результате изучения математических дисциплин бакалавр должен обладать:
– универсальными математическими компетенциями, среди которых общенаучные, инструментальные, социально-личностные;
– предметно-социальными математическими компетенциями, представляющими собой, по сути, систему усвоенных математических знаний, умений, навыков, а так же способности бакалавров применять их в своей профессиональной деятельности.
Обратимся к ФГОС ВПО по направлению подготовки 141100 Энергетическое машиностроение [4]. В качестве требований к результату освоения математических дисциплин из общего списка компетенций бакалавра-инженера, перечисленных в стандарте, можно выделить три общекультурные и две профессиональные компетенции. К каждой из них подобраны соответствующие математические компетенции, причем универсальные математические компетенции рассматриваются нами как составляющая часть общекультурных компетенций ОК-1, ОК-2, ОК-6; предметно-социальные математические компетенции – как часть профессиональных компетенций ПК-2, ПК-3 (табл. 1).
Таблица 1
Компетенции бакалавра-инженера
|
Общекультурные и профессиональные компетенции инженера |
Математические компетенции инженера |
|
Способность к обобщению, анализу, восприятию информации, постановке цели и выбору путей ее достижения (ОК-1). |
Обладать математическим мышлением, математической культурой как частью профессиональной и общечеловеческой культуры; владеть способами доказательств утверждений и теорем как основной составляющей когнитивной и коммуникативной функций; владеть методами анализа и синтеза изучаемых явлений и процессов. |
|
Умение логически верно, аргументировано и ясно строить устную и письменную речь (ОК-2). |
Владеть математической логикой, необходимой для формирования суждений по соответствующим профессиональным, социальным, научным и этическим проблемам; уметь представлять математические утверждения и их доказательства, задачи и их решения ясно и точно в терминах, понятных для профессиональной аудитории, как в письменной, так и устной форме. |
|
Способность в условиях развития науки и изменяющейся социальной практики к переоценке накопленного опыта, анализу своих возможностей, готовность приобретать новые знания, использовать различные средства и технологии обучения (ОК-6). |
Обладать способностью к критике и самокритике, умением работать в команде; быть готовым приобретать новые математические знания; владеть развитыми учебными навыками и готовностью к продолжению образования; |
|
Способность демонстрировать базовые знания в области естественнонаучных дисциплин и готовность использовать основные законы в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования (ПК-2). |
Иметь глубокие знания базовых математических дисциплин и проявлять высокую степень их понимания; демонстрировать понимание основных теорем и умение их доказывать; уметь решать математические задачи, аналогичные ранее изученным, но более высокого уровня сложности; уметь решать математические задачи из различных областей математики, которые требуют некоторой оригинальности мышления. |
|
Готовность выявлять естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности, и способность привлечь для их решения соответствующий физико-математический аппарат (ПК-3). |
Уметь формулировать на математическом языке задачи среднего уровня сложности, поставленные в нематематических терминах, и использовать превосходства этой переформулировки для их решения; обладать способностью к применению знаний на практике, в том числе умением составлять математические модели типовых профессиональных задач и находить способы их решений, интерпретировать профессиональный (физический) смысл полученного математического результата. |
Предметно-социальные математические компетенции, являющиеся частью профессиональных компетенций бакалавров-инженеров, условно можно разделить на три категории:
● понятийные – знание базовых определений и теорем; способность применять эти знания для решения задач;
● операционно-алгоритмические – знание основных алгоритмов; способность определять круг задач, для которых применим конкретный алгоритм; способность применять требуемый алгоритм;
● прикладные – видение прикладного аспекта дисциплины; способность применять базовые знания для решения задач прикладного характера.
Следовательно, для успешного формирования математических компетенций базовая направленность математических курсов должна находить свое выражение в явном выделении фундаментальных понятий; в активном использовании метода математического моделирования, заключающемся в составлении моделей и применении этих моделей на практике. Прикладная ориентация курса должна находить свое выражение в усилении внимания к приложениям математики и к методам приближенного вычисления. Необходимо, чтобы в каждом модуле были представлены задачи, приводящие к необходимости использования новой математической модели; изложены основы нового математического аппарата; указаны пути применения построенной математической модели к решению практических задач.
Математическая, как и любая предметная компетенция, не может быть сформулирована на одном, общим для всех и строго заданном уровне. В ФГОС ВПО (Раздел VIII. Оценка качества освоения основных образовательных программ бакалавриата) указано, что для аттестации обучающихся на соответствие их персональных достижений поэтапным требованиям соответствующей ООП (текущий контроль успеваемости и промежуточная аттестация) создаются фонды оценочных средств, включающие типовые задания, контрольные работы, тесты и методы контроля, позволяющие оценить знания, умения и уровень приобретенных компетенций. Фонды оценочных средств разрабатываются и утверждаются вузом [4].
В методических рекомендациях для профессорско-преподавательских коллективов вузов, размещенных на портале ФГОС ВПО [1], зафиксированы следующие уровни сформированности компетенций у выпускников: как минимум, пороговый уровень – обязательный для всех студентов-выпускников по завершении освоения основных образовательных программ ВПО, а также повышенные (один или несколько) уровни (относительно порогового). Назначение уровней компетенций – выстраивание этапности обучения на основе постепенного повышения сложности задач, которые способны самостоятельно решать студенты.
По характеру формулировок математических компетенций их можно разбить на следующие группы:
● Формулировки компетенций предполагают необходимость разделения на уровни в зависимости от сложности упомянутых математических теорий, утверждений, задач и т.п. уметь использовать знания математических дисциплин на соответствующем уровне – базовом, повышенном, продвинутом;
● демонстрировать способность к абстракции, в том числе умение логически развивать отдельные формальные теории и устанавливать связь между ними;
● уметь ясно и точно представлять математические утверждения и их доказательства, задачи и их решения;
● уметь решать математические задачи из различных областей математики, которые требуют некоторой оригинальности мышления.
2. В формулировках компетенций упомянуты различные уровни достижения без четкой градации.
● уметь переводить на математический язык простейшие проблемы, поставленные в терминах других предметных областей;
● уметь формулировать на математическом языке проблемы среднего уровня сложности, поставленные в нематематических терминах.
3. Формулировки компетенций предполагают заведомо повышенный уровень, но представляется возможным выделить в них пороговый (минимальный) уровень.
● уметь решать математические задачи, аналогичные ранее изученным, но более высокого уровня сложности (пороговый уровень – уметь решать математические задачи, аналогичные ранее изученным);
● уметь проводить доказательства математических утверждений, не аналогичных ранее изученным, но тесно примыкающих к ним (пороговый уровень – приводить доказательства математических утверждений, аналогичных ранее изученным);
● демонстрировать понимание основных теорем из различных математических курсов и умение их доказывать (пороговый уровень – демонстрировать понимание основных теорем).
На основании проведенного анализа нами выделены критерии определения трех уровней математических компетенций (пороговый, продвинутый, высокий). Эти критерии, в свою очередь, послужили критериями отбора заданий для текущего контроля, являющимися средством оценки уровней достижения математических компетенций бакалавров-инженеров (табл. 2).
Таблица 2
Критерии определения уровней математических компетенций и отбора заданий для текущего контроля
|
Уровень |
Критерий определения уровня |
Критерий отбора заданий |
|
I пороговый |
Знать и понимать основные определения и теоремы курса; знать и понимать актуальные проблемы математики в рамках учебной информации; уметь изложить основные теоретические проблемы математики; уметь найти необходимую информацию по математике; уметь репродуцировать имеющуюся информацию; быть готовым к воспроизведению полученных знаний. |
Задачи, требующие умения применять в знакомой ситуации известные факты, стандартные приемы, распознавать математические объекты и свойства, применять известные алгоритмы и технические навыки. |
|
II продвинутый |
Уметь доказывать изученные теоремы; уметь доказывать математические утверждения, аналогичные ранее изученным; уметь анализировать и синтезировать полученную информацию; знать и понимать междисциплинарные основы математики; уметь использовать математические термины в устной беседе. |
Задачи, которые не являются типичными, но знакомы студентам или выходят за рамки известного лишь в небольшой степени. |
|
III высокий |
Знать и понимать актуальные проблемы математики, выходящие за рамки учебной информации; уметь применять различные методы и технологии для решения задач; уметь представлять, объяснять, анализировать и интерпретировать полученные результаты; уметь доказывать математические утверждения, не аналогичные ранее изученным; уметь вести научную дискуссию; уметь устанавливать междисциплинарные связи; уметь систематизировать полученную информацию. |
Задачи, для решения которых требуются определенная интуиция, размышления и творчество в выборе математического инструментария, интегрирование знаний из разных разделов курса математики, самостоятельная разработка алгоритма действий. |
Например, при изучении темы «Дифференциал функции», отобраны и разделены согласно определенным уровням следующие задачи для самостоятельной работы [2].
Задачи на формирование понятийных математических компетенций:
Уровень 1) Известно, что в некоторой точке x0 значение производной функции y = f(x) равно 5. Найдите значение дифференциала функции в точке x0 при Δx = – 0,3.
Требуется уметь применить в знакомой ситуации известную формулу dy = y’Δx (непосредственная подстановка значений в формулу).
Уровень 2) Дана функция f(x) = x2. Известно, что в некоторой точке приращению независимой переменной соответствует главная часть приращения функции, равная (– 0,8). Найти начальное значение независимой переменной.
Требуется проанализировать условие задачи; знать определение дифференциала функции; понять, какую формулу необходимо применить для решения задачи; уметь выразить из нее искомое значение.
Уровень 3) Найдите дифференциал функции у = x3 – 2x2 + x + 3 двумя способами: а) как главную линейную часть приращения функции; б) при помощи производной. Сравните полученные результаты. Могли они оказаться различными?
Требуется знать и глубоко понимать определение дифференциала функции и приращения функции; уметь вычислять дифференциал различными способами; уметь выполнять алгебраические преобразования, уметь представлять, объяснять анализировать и интерпретировать полученные результаты.
Задачи на формирование операционно-алгоритмических математических компетенций:
Уровень 1) Найдите дифференциал функции y = sin ln x.
Уровень 2) Дана функция y = sin z , где z = ax. Выразите d2 y через:
а) z и dz, б) xи dx.
Уровень 3) Докажите, что функция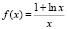 
удовлетворяет уравнению 
.
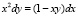Задачи этого типа направлены на закрепление алгоритмических умений – в данном случае умение вычислять дифференциал функции. Как правило, они отличаются варьированием условий, либо уровнем сложности, проводимых в ходе вычислений математических преобразований.
Задачи на формирование прикладных математических компетенций:
Уровень 1) Вычислите приближенно с помощью дифференциала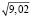 
.
Уровень 2) Найдите приращение и дифференциал функции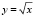 
в при x = 10 и Δx = 0,1. Вычислите абсолютную и относительную погрешности, которые допускаются при замене функции ее дифференциалом. Сделайте чертеж. Объясните геометрический смысл дифференциала.
Уровень 3) Период колебания маятника (в секундах) определяется по формуле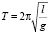 
, где l – длина маятника (в сантиметрах) и g = 981 см/с2. На сколько нужно изменить длину маятника l = 20 см, чтобы период колебания увеличился на 0,05 с?
Предложенные задачи на использование дифференциала функции в приближенных вычислениях. В первых двух задачах для приближенных вычислени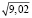й 
и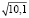 
необходимо использовать дифференциал одной и той же функции 
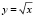. Однако во второй задаче есть дополнительные условия – вычислить приращение функции, найти погрешность и проинтерпретировать полученные результаты. Для решения третьей – физической задачи студентам необходимо самостоятельно построить математическую модель и разработать алгоритм решения, а также представить и объяснить результат.