При нахождении экстремума функции нескольких переменных следует помнить, что её аргументы могут быть или независимыми, или зависимыми переменными. В случае независимых переменных говорят, что решается задача безусловной оптимизации (задача на безусловный экстремум).
В данной статье рассматривается экстремум целевой функции, аргументы которой зависимы между собой.
Задача, означенная в заголовке, – это задача минимизации (или максимизации) заданной функции f на множестве X, определяемом системой конечного числа уравнений («связей»):
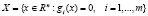 .
.
Запишем эту задачу в виде
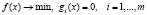 . (1)
. (1)
В некоторых случаях возможен следующий подход к отысканию решения задачи (1). Допустимое множество представляет собой систему из m уравнений с n неизвестными, при этом обычно 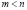 . Если из этой системы удается m переменных выразить через остальные
. Если из этой системы удается m переменных выразить через остальные 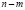 переменных, то относительно них получается задача безусловной оптимизации.
переменных, то относительно них получается задача безусловной оптимизации.
Пример 3.1. Почта США принимает посылки в виде ящиков, у которых длина и обхват поперек ее в сумме не превышают 72 дюйма (один дюйм – это 25.4 мм). При каких допустимых размерах посылки ее объем наибольший?
Решение. В очевидных обозначениях имеем задачу 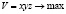 при условиях
при условиях 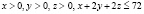 . Ясно, что здесь достаточно нестрогое неравенство заменить равенством, и мы имеем задачу (1), в которой
. Ясно, что здесь достаточно нестрогое неравенство заменить равенством, и мы имеем задачу (1), в которой
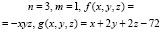 .
.
Выразив  из уравнения связи, придем к задаче безусловной оптимизации функции двух переменных (как говорят, понизим размерность задачи)
из уравнения связи, придем к задаче безусловной оптимизации функции двух переменных (как говорят, понизим размерность задачи)
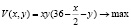 ,
,
решением которой будет точка (24; 12).
В этом примере исследование условного экстремума свелось к уже рассмотренному исследованию обычного экстремума функции меньшего числа переменных.
Описанный метод исключения переменных имеет ограниченную область применения, поскольку выразить группу одних переменных через остальные – процедура не всегда однозначная и далеко не всегда легко осуществимая. Более универсальным является метод Лагранжа, основанный на использовании условий экстремума непосредственно для задачи (1).
По определению, функция Лагранжа задачи (1) – это функция
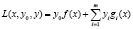 , (2)
, (2)
где 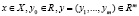 . Пусть
. Пусть 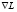 – градиент функции Лагранжа по
– градиент функции Лагранжа по  ,
, 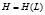 – ее гессиан по
– ее гессиан по 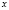 . Следующая теорема (без вывода), лежащая в основе метода Лагранжа, является центральным фактом классической теории условного экстремума.
. Следующая теорема (без вывода), лежащая в основе метода Лагранжа, является центральным фактом классической теории условного экстремума.
Теорема 3.1 (необходимое условие минимума первого порядка, или принцип Лагранжа). Пусть функции 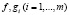 – гладкие в некоторой окрестности точки
– гладкие в некоторой окрестности точки 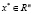 , являющейся локальным решением задачи (1). Тогда в
, являющейся локальным решением задачи (1). Тогда в 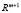 существует ненулевой вектор
существует ненулевой вектор 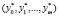 такой, что
такой, что 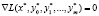 .
.
Здесь последнее равенство имеет ясный геометрический смысл: с учетом (2) оно означает, что градиенты функций 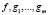 в точке
в точке 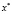 являются линейно зависимыми. В частности, если
являются линейно зависимыми. В частности, если 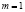 , то градиенты
, то градиенты 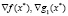 должны быть коллинеарными. Напомним, что эти градиенты, если они ненулевые, направлены ортогонально к поверхностям уровня
должны быть коллинеарными. Напомним, что эти градиенты, если они ненулевые, направлены ортогонально к поверхностям уровня 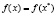 и
и 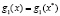 соответственно, причем их коллинеарность говорит о том, что решение
соответственно, причем их коллинеарность говорит о том, что решение 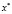 должно быть точкой касания данных поверхностей (при
должно быть точкой касания данных поверхностей (при 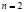 – линий уровня). Фактически это необходимое условие, или «принцип касания».
– линий уровня). Фактически это необходимое условие, или «принцип касания».
Любое дополнительное предположение о задаче (1), обеспечивающее в теореме 3.1 случай 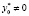 , принято называть условием регулярности. При наличии такого условия и саму задачу (1) называют регулярной. Для нее достаточно рассматривать лишь регулярную функцию Лагранжа
, принято называть условием регулярности. При наличии такого условия и саму задачу (1) называют регулярной. Для нее достаточно рассматривать лишь регулярную функцию Лагранжа
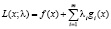 . (3)
. (3)
Самым главным примером условия регулярности является условие линейной независимости градиентов функций gi на допустимом множестве.
Теорема 3.2 (достаточное условие минимума второго порядка). Пусть функции 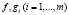 , дважды гладкие в окрестности точки
, дважды гладкие в окрестности точки 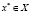 , гладкие и градиенты
, гладкие и градиенты 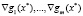 линейно независимы. Пусть существует вектор
линейно независимы. Пусть существует вектор 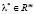 со свойствами:
со свойствами:
1) для функции (3) 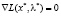 ;
;
2) матрица Гессе 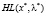 положительно определена на множестве векторов
положительно определена на множестве векторов
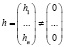 ,
,
удовлетворяющих условию
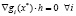 . (4)
. (4)
Тогда 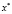 – строгое локальное решение задачи (1).
– строгое локальное решение задачи (1).
Условие (4) означает, что вектор h ортогонален к линейному пространству, натянутому на градиенты 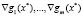 . Поэтому его называют условием ортогональности. Ясно, что если задачу (1) заменить задачей максимизации, а в условии 2) потребовать, чтобы матрица Гессе была отрицательно определенной, то в точке
. Поэтому его называют условием ортогональности. Ясно, что если задачу (1) заменить задачей максимизации, а в условии 2) потребовать, чтобы матрица Гессе была отрицательно определенной, то в точке 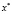 целевая функция имеет строгий локальный максимум.
целевая функция имеет строгий локальный максимум.
На практике обычно имеет место случай, когда целевая функция f и все функции gi, дважды гладкие в некоторой области 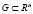 , содержащей допустимое множество, причем градиенты функций gi линейно независимы. Проверив эту независимость, далее для решения задачи (1) надлежит сделать следующее.
, содержащей допустимое множество, причем градиенты функций gi линейно независимы. Проверив эту независимость, далее для решения задачи (1) надлежит сделать следующее.
1. Составить функцию Лагранжа (3) и найти ее градиент по x.
2. Потребовать, чтобы построенный градиент был равен нулю. К полученной системе уравнений добавить уравнения связей и решить возникшую систему. Пусть 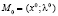 – одно из этих решений (стационарная точка функции Лагранжа по всем переменным). Числа
– одно из этих решений (стационарная точка функции Лагранжа по всем переменным). Числа 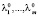 называются множителями Лагранжа, соответствующими точке
называются множителями Лагранжа, соответствующими точке 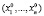 . Эта точка является «подозрительной» на экстремум целевой функции.
. Эта точка является «подозрительной» на экстремум целевой функции.
3. Исследовать на знакоопределенность гессиан функции Лагранжа по x в точке 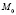 при условии ортогональности и сделать заключение в соответствии с теоремой 3.2.
при условии ортогональности и сделать заключение в соответствии с теоремой 3.2.
Вектор h в теореме 3.2, как и в случае безусловной оптимизации, состоит из приращений аргументов, т.е. их дифференциалов:
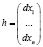 .
.
Тогда условие ортогональности (4) можно записать в виде
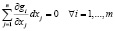 .
.
На шаге 3 указанной схемы при этих условиях надо исследовать на знакоопределенность квадратичную форму матрицы Гессе 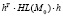 , т.е. второй дифференциал
, т.е. второй дифференциал 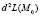 функции Лагранжа по x.
функции Лагранжа по x.
Пример 3.2. Найти экстремальные значения функции 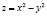 на прямой
на прямой 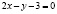 .
.
Решение. Имеем случай 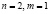 . Условие «градиенты функций gi линейно независимы» в данном случае означает, что градиент функции
. Условие «градиенты функций gi линейно независимы» в данном случае означает, что градиент функции 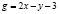 отличен от нуля. Но это так, ибо
отличен от нуля. Но это так, ибо 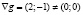 . Далее действуем в соответствии с описанной трехшаговой схемой.
. Далее действуем в соответствии с описанной трехшаговой схемой.
1. Составим регулярную функцию Лагранжа
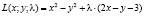 ,
,
найдем ее градиент по переменным 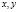 :
:
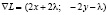 .
.
2. Решением системы уравнений
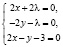 .
.
является единственная точка 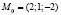 .
.
3. Составим матрицу Гессе функции Лагранжа. В любой точке, в частности, в найденной, она равна
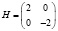 .
.
Отсюда 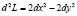 . Полученная квадратичная форма пока знакопеременная. Например, ее значение при
. Полученная квадратичная форма пока знакопеременная. Например, ее значение при 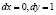 равно –2, а при
равно –2, а при 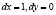 оно равно 2. Но ведь мы не учитывали уравнение связи. Из него имеем
оно равно 2. Но ведь мы не учитывали уравнение связи. Из него имеем 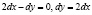 . Тогда
. Тогда 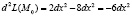 , т.е. второй дифференциал есть отрицательно определенная квадратичная форма. Следовательно, точка
, т.е. второй дифференциал есть отрицательно определенная квадратичная форма. Следовательно, точка 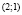 является точкой локального условного максимума целевой функции, равного 3.
является точкой локального условного максимума целевой функции, равного 3.
Пример 3.3. Найти точки условного экстремума функции 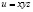 при условиях
при условиях
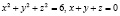 .
.
Решение. Градиенты функций 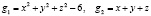 (выпишите их) коллинеарны при
(выпишите их) коллинеарны при 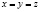 . Но точка с равными координатами не может лежать на допустимом множестве X, описываемом равенствами
. Но точка с равными координатами не может лежать на допустимом множестве X, описываемом равенствами 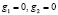 . Следовательно, можно решать регулярную задачу.
. Следовательно, можно решать регулярную задачу.
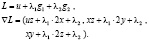
Решаем систему уравнений
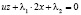 , (5)
, (5)
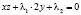 , (6)
, (6)
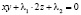 , (7)
, (7)
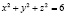 , (8)
, (8)
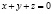 . (9)
. (9)
Как наиболее эффективно решить эту систему? Один из подходов состоит в следующем: умножим обе части первого уравнения на x, второго – на y, третьего – на z, после чего все три уравнения сложим. В силу (8), (9) получим
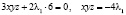 . (10)
. (10)
После этого уравнения (5) – (7) примут вид
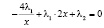 , (5а)
, (5а)
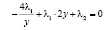 , (6а)
, (6а)
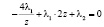 , (7а)
, (7а)
Из уравнения (5а) вычтем (6а). После некоторых преобразований получим
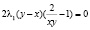 .
.
Здесь множитель Лагранжа не должен быть нулевым, поэтому 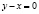 или
или 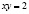 . Добавляя к последнему равенству уравнения связи, придем к несовместной системе. Но система уравнений из (8) и (9) и
. Добавляя к последнему равенству уравнения связи, придем к несовместной системе. Но система уравнений из (8) и (9) и 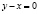 имеет два решения
имеет два решения 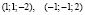 .
.
Повторяя затем поочередно описанную процедуру с уравнениями (5а), (7а) и (6а), (7а), получим еще 4 решения. Итого будем иметь 6 точек, «подозрительных» на экстремум целевой функции:
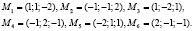
Составим гессиан функции Лагранжа по x,y,z в произвольной точке:
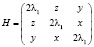 .
.
Точке M1, согласно (10), соответствует множитель Лагранжа 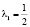 . Исследуем гессиан
. Исследуем гессиан
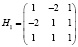 .
.
Из равенств (8), (9) имеем
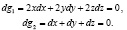
Точке 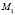 соответствуют равенства
соответствуют равенства
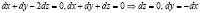 .
.
Второй дифференциал функции Лагранжа, или, что то же, квадратичная форма матрицы 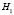 , имеет вид
, имеет вид
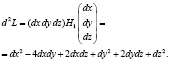
Или
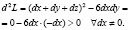
Следовательно, в точке 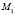 целевая функция имеет минимум, равный – 2. Таков же результат в отношении точек
целевая функция имеет минимум, равный – 2. Таков же результат в отношении точек 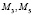 . В остальных точках будет максимум, равный 2.
. В остальных точках будет максимум, равный 2.
Выделение точек условного экстремума входит составной частью в решение задачи о нахождении наибольшего и наименьшего значений функции в замкнутой ограниченной области 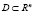 . Используется следующий факт: экстремум дифференцируемой функции достигается либо во внутренней стационарной точке области, либо на ее границе.
. Используется следующий факт: экстремум дифференцируемой функции достигается либо во внутренней стационарной точке области, либо на ее границе.
Пример 3.4. Найти наибольшее и наименьшее значения функции
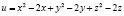
в полушаре
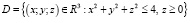 .
.
Решение. Приведем краткое решение, опуская детали, которые читателю следует воспроизвести. Единственная стационарная точка 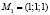 лежит внутри области, поэтому займемся исследованием поведения функции на ее границе. Эта граница состоит из полусферы
лежит внутри области, поэтому займемся исследованием поведения функции на ее границе. Эта граница состоит из полусферы
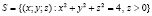
и круга
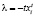 .
.
Применяя метод Лагранжа, нетрудно убедиться в том, что на полусфере единственной возможной точкой экстремума является
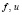 .
.
Внутри круга находится только одна стационарная точка
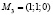 .
.
Снова, применяя метод Лагранжа, обнаруживаем две «подозрительные» на экстремум точки границы круга
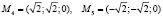 .
.
Итак, искомые значения могут достигаться только в указанных пяти точках. Составим вектор значений целевой функции в этих точках
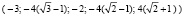 ,
,
найдем его наименьший и наибольший элементы. Получим ответ: наименьшее значение, равное – 3, достигается в первой точке; наибольшее – в последней точке и равно 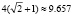 .
.
В заключение статьи сделаем важное замечание по применению метода Лагранжа. Используя его, надо аккуратно проверять условие линейной независимости градиентов функций, задающих уравнения связи. Если это условие не выполняется, то метод может и не дать некоторых точек экстремума целевой функции. Например, пусть на плоскости требуется найти расстояние от начала координат до полукубической параболы 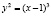 . Другими словами, надо найти минимум функции цели
. Другими словами, надо найти минимум функции цели 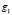 при условии
при условии 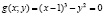 . Геометрически очевидно, что искомое расстояние равно 1 и достигается в точке
. Геометрически очевидно, что искомое расстояние равно 1 и достигается в точке 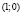 , в которой градиент функции
, в которой градиент функции 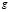 нулевой. Но с помощью правила Лагранжа мы не можем получить эту точку, так как системе уравнений
нулевой. Но с помощью правила Лагранжа мы не можем получить эту точку, так как системе уравнений
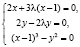
ее координаты не удовлетворяют.
Более обстоятельный разговор об использовании метода множителей Лагранжа читатель найдет в нашей работе [1].

