Лабораторный практикум по курсу «Процессы и аппараты химической технологии» [1] выполняется студентами с целью закрепления теоретических знаний, изучения современных методов экспериментального исследования гидромеханических, тепловых и массообменных процессов. При выполнении лабораторных работ студенты используют математические модели процессов, а также лабораторные установки, оснащенные датчиками для измерения различных параметров (температур, давлений, скорости, веса и т.д.). В лабораторных экспериментах определяются и исследуются кинетические закономерности изучаемых процессов. При моделировании исследуемых процессов и обработке результатов экспериментов применяются, как универсальные, так и специальные компьютерные программы [1].
Однако возможности традиционно используемых лабораторных установок ограничены, во-первых, временными рамками занятий, а во-вторых, не всегда позволяют изучать процессы с учетом всех влияющих факторов. Устранить этот недостаток позволяет использование в лабораторном практикуме информационных технологий – виртуальных лабораторных работ [2]. Причем виртуальный лабораторный практикум призван не заменить классический, а дополнить и расширить его за счет интерактивного обучения, а значит существенно повысить качество освоения дисциплины.
Рассмотрим сочетание активного и интерактивного (виртуального) лабораторного практикума на примере лабораторной работы «Испытание лабораторного вакуум-фильтра», которая знакомит студентов с одним из важнейших разделов гидромеханических процессов – «Разделение неоднородных систем методом фильтрования».
Схема лабораторной установки представлена на рис. 1.
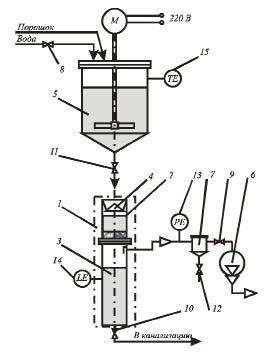
Рис. 1. Схема лабораторной установки: 1 – нутч-фильтр; 2 – царга; 3 – сборник фильтрата; 4 – распределитель жидкости; 5 – бачок для суспензии; 6 – вакуум-насос; 7 – брызгоуловитель; 8, 9, 10 – вентили; 11, 12 – краны; 13 – вакуумметр; 14 – водомерная линейка; 15 – термометр
Основными элементами установки являются: нутч-фильтр 1, включающий царгу 2, сборник фильтрата 3 и распределитель 4; бачок для суспензии с мешалкой – 5; вакуум-насос – 6; брызгоуловитель – 7. Царга 2 и сборник фильтрата 3 разделяются фильтрующей перегородкой и опорной решеткой и соединяются между собой с помощью фланцевого соединения. Для измерения объема фильтрата сборник 3 снабжен водомерной линейкой 14, а для измерения вакуума – вакуумметром 13. Температура суспензии в бачке замеряется с помощью термометра 15. Вакуум в установке создается вакуум-насосом 6. Установка оснащена брызгоуловителем 7 и запорной арматурой 8 –12.
Целью работы является определение констант фильтрования – удельного сопротивления осадка (индивидуальная характеристика осадка) и сопротивления фильтровальной перегородки (индивидуальная характеристика перегородки), которые необходимо знать при расчете и подборе промышленных фильтров для разделения суспензий.
В основе лабораторной работы лежит основное кинетическое уравнение фильтрования [3]
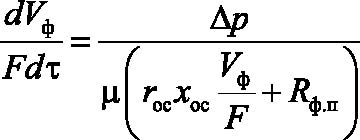 , (1)
, (1)
где Vф – объем фильтрата, м3; F – площадь фильтрования, м2; t – продолжительность фильтрования, с; Dр – разность давлений, Па; m – вязкость жидкой фазы суспензии, Па×с; Rф.п – сопротивление фильтровальной перегородки, м-1; rос – удельное сопротивление осадка (сопротивление, оказываемое потоку фильтрата равномерным слоем осадка толщиной 1 м), м-2; xос – удельный объем осадка (объем осадка, отнесенный к объему фильтрата), м3/м3.
На лабораторной установке фильтрование идет в режиме фильтрования с постоянным перепадом давления Dр = const. Для этого режима фильтрования после разделения переменных и интегрирования уравнения (1) получим
![]() . (2)
. (2)
В уравнении (2) величина Vф/F представляет собой удельный объем фильтрата – количество фильтрата на единицу поверхности фильтрования. Если обозначить эту величину через q, уравнение (2) примет вид
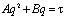 , (3)
, (3)
где А, В – коэффициенты уравнения, включающие константы фильтрования и определяемые по формулам
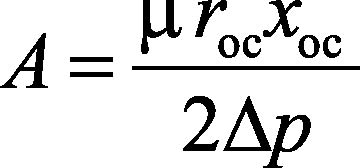 , (4)
, (4)
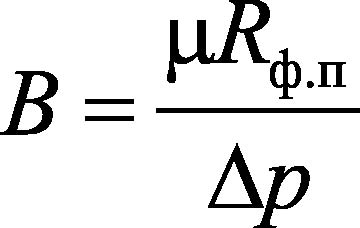 . (5)
. (5)
Уравнение (3) может быть преобразовано в линейную зависимость:
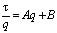 . (6)
. (6)
Эта зависимость на практике используется для нахождения констант фильтрования.
Первичными экспериментальными данными в работе являются данные по накоплению фильтрата в сборнике с течением времени Vф = f(t). По результатам обработки этих данных с использованием электронных таблиц EXCEL строят график зависимости (6) в координатах t/q и q. На рис. 2 в качестве примера приведены результаты обработки одного из опытов.
На рис. 2 приведено уравнение, которое с достаточной точностью описывает зависимость t/q = f(q). Следует отметить, что аналогичный подход к обработке экспериментальных данных, получаемых студентами, используется и при выполнении других лабораторных работ [1].
Искомые константы фильтрования легко определяются через численные значения коэффициентов:
– А = 689,58 (тангенс угла наклона прямой);
– В = 546,43 (отрезок, отсекаемый прямой на оси ординат).
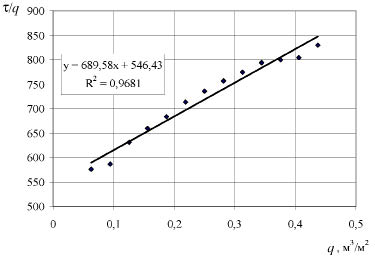
Рис. 2. График к определению констант фильтрования
По величине коэффициента А определяется удельное сопротивление осадка rос
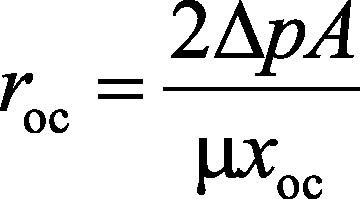 , (7)
, (7)
Сопротивление фильтрующей перегородки Rф.п определяется по коэффициенту В
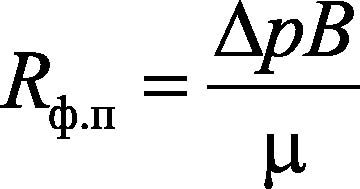 . (8)
. (8)
Так для условий экспериментов, представленных на рис. 2, значения констант фильтрования составляют
rос = 1,96 · 1012 м–2;
Rф.п. = 1,98 · 1010 м–1.
Полученные значения констант сопоставляются студентом с аналогичными характеристиками в справочных материалах по фильтрованию [4, 5].
Интерактивная (виртуальная) часть работы выполняется на компьютере. Виртуальная модель лабораторной работы разработана в среде Flash (рис. 3).
Программа обеспечивает:
• интерактивное ознакомление с выполнением лабораторной работы (рис. 4);
• ответы на простейшие тесты (рис. 5), по результатам которых программа дает разрешение на выполнение интерактивной части;
• задачу первичных исходных параметров процесса в достаточно широком диапазоне (рис. 6);
• выполнение интерактивного варианта лабораторной работы аналогично последовательности выполнения активной работы, при этом получаем тех же самые опытные величины (рис. 7).
Рис. 3. Заставки виртуальной работы

Рис. 4. Методические материалы к работе
Рис. 5. Тестовые материалы к работе
Рис. 6. Задача первичных исходных данных
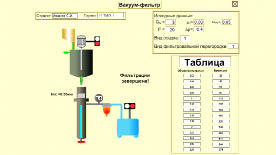
Рис. 7. Результаты интерактивной части работы
Обработка результатов интерактивной части лабораторной проводится студентами так же, как и активной. Строится график зависимости t/q = f(q) (рис. 2) и определяются по формулам (7) и (8) константы фильтрования rос и Rфп. Результаты расчетов констант сравниваются с величинами, заложенными в алгоритм программы, и характеризующими конкретные виды осадка и фильтровальной перегородки.
Проведение интерактивной части работы при разных исходных данных позволяет наглядно продемонстрировать студентам зависимость констант от вида осадка и фильтровальной перегородки, и их не зависимость от условий проведения опытов.
Такой комплексный вариант выполнения лабораторных работ позволяет расширить возможности традиционно используемого лабораторного практикума и в ходе его выполнения изучать процессы с учетом всех определяющих их факторов, что, в свою очередь, развивает творческий подход студентов к работе в лаборатории.

