Постановка задачи
Для решения задачи о моделировании упругих волн в деформируемых областях сложной формы рассмотрим некоторое тело Г в прямоугольной декартовой системе координат XOY (рис. 1), которому в начальный момент времени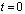 
сообщается механическое воздействие. Предположим, что тело Г изготовлено из однородного изотропного материала, подчиняющегося упругому закону Гука при малых упругих деформациях.
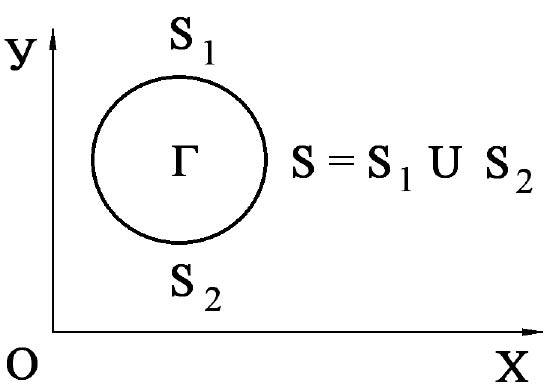
Рис. 1. Некоторое тело Г в прямоугольной декартовой системе координат XOY
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид
, 
,
,
,
, 
,
, 
, 
,
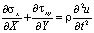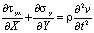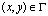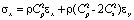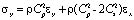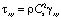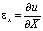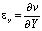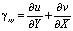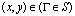, (1)
где 
, 
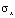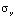и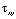 
– компоненты тензора упругих напряжени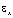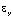й; 
, 
и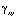 
– компоненты тензора упругих деформаций; u и v – составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; 
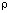– плотность материала; 
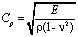– скорость продольной упругой волны; 
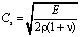– скорость поперечной упругой волны; 
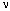– коэффициент Пуассона; E – модуль упругости; 
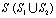– граничный контур тела Г.
Систему (1) в области, занимаемой телом Г, следует интегрировать при начальных и граничных условиях.
Разработка численного метода, алгоритма и комплекса программ
Конечноэлементное моделирование позволяет задачу с бесконечным числом неизвестных привести к задаче с конечным числом неизвестных, решение которой принципиально возможно на вычислительных машинах.
С помощью конечноэлементного моделирования получаем приближенное решение дифференциальной задачи, то есть задачи с начальными и граничными условиями.
В работах [1–10] приводится информация о численном моделировании нестационарного динамического напряженного состояния сложных систем с помощью разработанного метода и о постановке безопасности сложных систем.
Для решения двумерной нестационарной динамической задачи математической теории упругости с начальными и граничными условиями (1) используем метод конечных элементов в перемещениях.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в теории упругости
, 
,
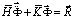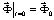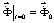, (2)
где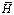 
– диагональная матрица инерции; 
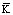– матрица жесткости; 
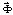– вектор узловых упругих перемещений; 
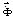– вектор узловых упругих скоростей перемещений; 
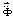– вектор узловых упругих ускорений; 
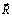– вектор внешних узловых упругих сил.
Интегрируя уравнения (2) конечноэлементным вариантом метода Галеркина, получим явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
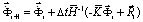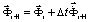. (3)
Шаг по временной переменной координате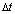 
выбирается из следующего соотношения
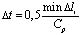
, (4)
где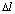 
– длина стороны конечного элемента.
На основе метода конечных элементов в перемещениях разработана методика, разработан алгоритм и составлен комплекс программ для решения двумерных линейных и нелинейных задач при различных начальных и граничных условиях, для областей сложной формы. Комплексы программ написаны на алгоритмическом языке Фортран-90.
В работах приведена информация о достоверности численного моделирования нестационарных волн напряжений в областях различной формы с помощью разработанного метода, алгоритма и комплекса программ [1–4, 9–10].
Решение задачи о воздействии взрывной волны в объекте хранения опасных веществ с полостью в виде прямоугольника (соотношение ширины к высоте один к пяти)
Рассмотрим задачу о воздействии взрывной волны (рис. 3) в объекте хранения опасных веществ с полостью в виде прямоугольника (соотношение ширины к высоте один к пяти) (рис. 2).
Расчеты проводились при следующих единицах измерения: килограмм-сила (кгс); сантиметр (см); секунда (с). Для перехода в другие единицы измерения были приняты следующие допущения: 1 кгс/см2 ≈ ≈ 0,1 МПа; 1 кгс с2/см4 ≈ 109 кг/м3.
По нормали к контуру IJKL приложено нормальное напряжение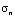 
, которое при 
(
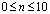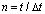) изменяется линейно от 0 до Р, а при 
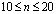от Р до 0 (
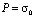). На контуре JI приложено нормальное напряжение 
(
= 
, 
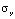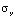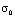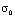= 0,1 МПа (1 кгс/см2)). На контуре KL приложено нормальное напряжение 
(
= 
, 
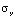= – 0,1 МПа (– 1 кгс/см2)).
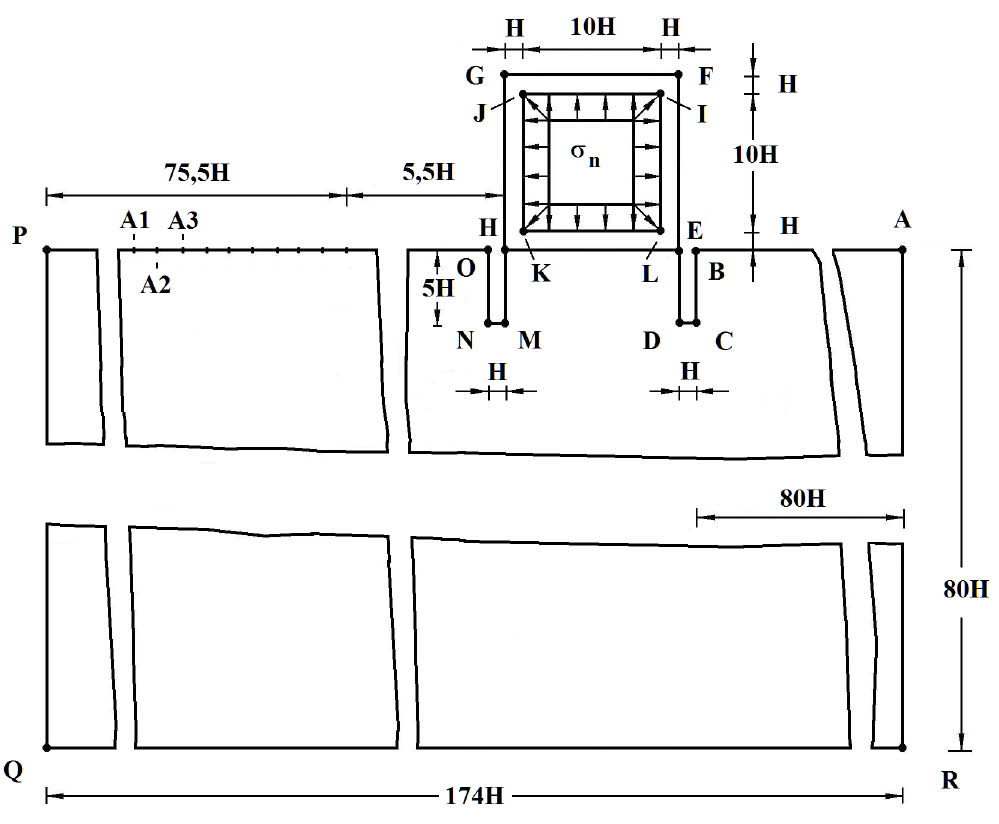
Рис. 2. Постановка задачи о воздействии упругой взрывной волны в объекте хранения опасных веществ с полостью в виде прямоугольника (соотношение ширины к высоте один к пяти)
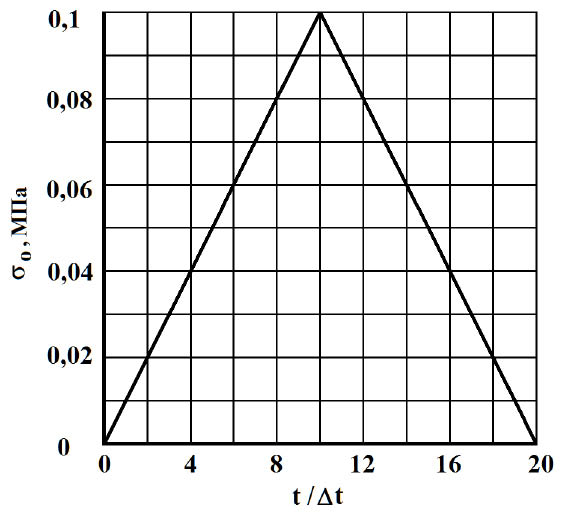
Рис. 3. Взрывное воздействие в виде типа дельта функции для задачи с полостью (соотношение ширины к высоте один к пяти)
На контуре IL приложено нормальное напряжение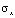 
(
= 
, 
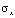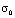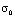= 0,1 МПа (1 кгс/см2)). На контуре JK приложено нормальное напряжение 
(
= 
, 
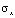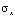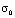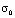= – 0,1 МПа (–1 кгс/см2)). Граничные условия для контура PQRA при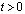 
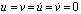. Отраженные волны от контура PQRA не доходят до исследуемых точек при 
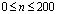. Контур ABCDEFGHMNOP свободен от нагрузок.
Расчеты проведены при следующих исходных данных: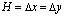 
; Δt = 1,393⋅10-6 с; E= 3,15⋅104 МПа (3,15⋅105 кгс/см2); ν=0,2; ρ=0,255⋅104 кг/м3 (0,255⋅10–5 кгс с2/см4); 
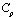= 3587 м/с; 
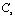= 2269 м/с.
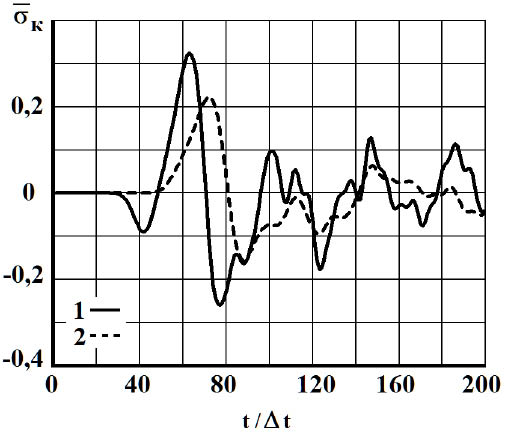
Рис. 4. Изменение упругого контурного напряжения 
во времени 
в точке А1: 1 – в задаче без полости; 2 – в задаче полостью (соотношение ширины к высоте один к пяти)
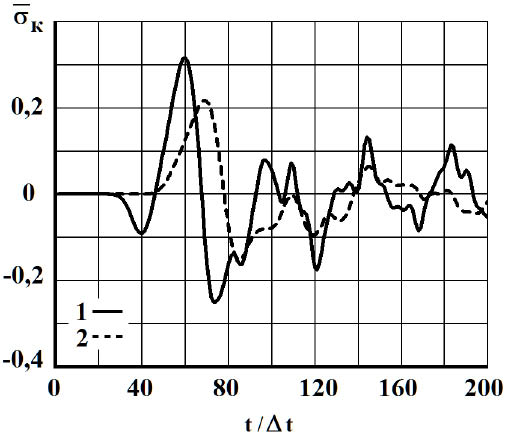
Рис. 5. Изменение упругого контурного напряжения 
во времени 
в точке А2: 1 – в задаче без полости; 2 – в задаче полостью (соотношение ширины к высоте один к пяти)
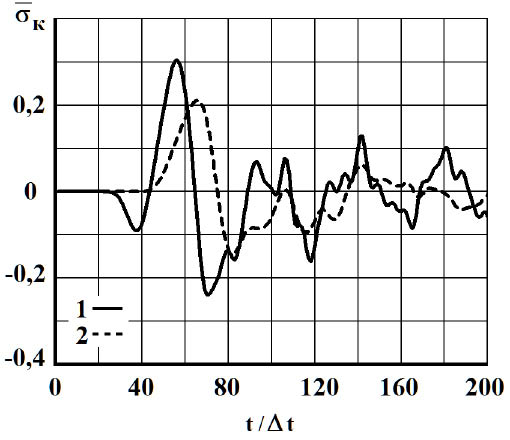
Рис. 6. Изменение упругого контурного напряжения 
во времени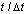 
в точке A3: 1 – в задаче без полости; 2 – в задаче полостью (соотношение ширины к высоте один к пяти)
Исследуемая расчетная область имеет 14250 узловых точек. Решается система уравнений из 57000 неизвестных.
На рис. 4–6 показано изменение упругого контурного напряжения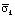 
(
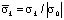) во времени n в точках 
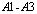(рис. 2), находящихся на свободной поверхности упругой полуплоскости (расстояние между точками: A1 и A2 равно H; A2 и A3 равно H).
Выводы
Полость, с соотношением ширины к высоте один к пяти, уменьшает величину упругого растягивающего контурного напряжения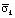 
в 1,462 раза. Полость, с соотношением ширины к высоте один к пяти, уменьшает величину упругого сжимающего контурного напряжения 
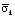в 1,66 раза.
Полость, с соотношением ширины к высоте один к пяти, уменьшает величину упругого растягивающего нормального напряжения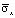 
в 1,51 раза. Полость, с соотношением ширины к высоте один к пяти, уменьшает величину упругого сжимающего нормального напряжения 
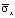в 1,84 раза.
Полость, с соотношением ширины к высоте один к пяти, уменьшает величину упругого растягивающего нормального напряжения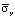 
в 1,52 раза. Полость, с соотношением ширины к высоте один к пяти, уменьшает величину упругого сжимающего нормального напряжения 
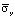в 1,81 раза.
Полость, с соотношением ширины к высоте один к пяти, уменьшает величину упругого растягивающего касательного напряжения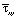 
в 1,81 раза. Полость, с соотношением ширины к высоте один к пяти, уменьшает величину упругого сжимающего касательного напряжения 
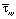в 1,54 раза.